Bài 4: Công của lực điện | Vật Lý | Chương 1: Điện tích, điện trường - Lớp 11 - Giáo Dục Việt Nam

Tưong tác tĩnh điện có nhiều điểm tưong đồng với tưong tác hấp dẫn. Ta sẽ thấy, công của lực điện cũng có những điểm tưong tự như công của trọng lực.

I- CÔNG CỦA LựC ĐIỆN

1. Đặc điểm của lực điện tác dụng lên một điện tích đặt trong điện trường đều

Đặt điện tích \( q \) dương \( (q > 0) \) tại một điểm \( M \) trong điện trường đều (Hình 4.1), nó sẽ chịu tác dụng của một lực điện \( \vec{F}=q \vec{E} \). Lực \( \vec{F} \) là lực không đổi, có phương song song với các đường sức điện, chiều hướng từ bản dương sang bản âm, độ lớn bằng \( q E \).

2. Công của lực điện trong điện trường đều

a) Điện tích \( q \) dương di chuyển theo đường thẳng \( M N \), làm với các đường sức điện một góc \( \alpha \), với \( M N=s \) (Hình 4.2). Ta có công của lực điện :

\[

\begin{array}{l}

A_{\mathrm{MN}}=\vec{F} \cdot \vec{S}=F s \cos \alpha \\

F=q E \text { và } s \cos \alpha=d \text { thì : }

\end{array}

\]

\[

A_{\mathrm{MN}}=q E d

\]

trong đó \( d=\overline{M H} \) là độ dài đại số, với \( M \) là hình chiếu của điểm đầu đường đi, \( H \) là hình chiếu của điểm cuối đường đi trên một đường sức. Ta chọn chiều dương cho \( \overline{M H} \) cùng chiều với chiều của đường sức.

Vì \( q > 0 \) nên \( \vec{F} \) cùng chiều với \( \vec{E} \). Do đó, \( \alpha \) vừa là góc giữa lực điện \( \vec{F} \) và độ dời \( \vec{s} \), vừa là góc giữa hướng của đường sức và hướng của độ dời \( \vec{s} \).

- Nếu \( \alpha < 90^{\circ} \) thì \( \cos \alpha > 0 \), do đó \( d > 0 \) ( \( \overline{M H} \) cùng chiều đường sức) và \( A_{\mathrm{MN}} > 0 \).

- Nếu \( \alpha > 90^{\circ} \) thì \( \cos \alpha < 0 \), do đó \( d < 0 \) ( \( \overline{M H} \) ngược chiều đường sức) và \( A_{\mathrm{MN}} < 0 \).

Trong trường hợp \( q < 0 \), ta có thể chứng minh công thức (4.1) vẫn đúng và quy ước về dấu của \( d \) vẫn giữ như trên.

1. b) Điện tích \( q \) di chuyển theo đường gấp khúc \( M P N \). Tương tự như trên, ta có :

\[

\begin{array}{c}

A_{\mathrm{MPN}}=F s_{1} \cos \alpha_{1}+F s_{2} \cos \alpha_{2} \\

\text { Với } s_{1} \cos \alpha_{1}+s_{2} \cos \alpha_{2}=d \text {, ta lại có }: \\

A_{\mathrm{MPN}}=q E d

\end{array}

\]

1. c) Kết quả trên có thể mở rộng cho các trường hợp đường đi từ \( M \) đến \( N \) là một đường gấp khúc hoặc đường cong.

Như vậy, công của lực điện trong sự di chuyển của điện tích trong điện truoòng đều tù \( M \) đến \( N \) là \( A_{\mathrm{MN}}=q E d \), không phụ thuộc vào hình dạng của đường đi mà chỉ phu thuộc vào vị trí của điểm đầu \( M \) và điểm cuối \( N \) của đuoòng đi. C

3. Công của lực điện trong sự di chuyển của điện tích trong điện trường bất ki

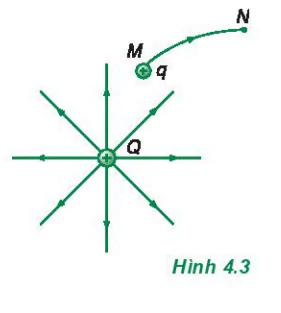
Người ta cũng đã chứng minh được rằng, công của lực điện trong sự di chuyển của một điện tích \( q \) từ điểm \( M \) đến điểm \( N \) trong một điện trường bất kì không phụ thuộc hình dạng đường đi từ \( M \) đến \( N \) mà chỉ phụ thuộc vào vị trí của \( M \) và \( N \) (Hình 4.3) Đây là một tính chất chung của điện trường tĩnh điện. Đặc tính này cho thấy, trường tĩnh điện là một trường thế. C2

II - THẾ NĂNG CỦA MỘT ĐIỆN TÍCH TRONG ĐIỆN TRƯỜNG

1. Khái niệm vể thế năng của một điện tích trong điện trường

C1 Hãy nêu sự tương tự giữa công của lực điện trong trường hợp này với công của trọng lực.

C2 Cho một điện tích điểm \( Q \) nằm tại tâm của một vòng tròn. Khi di chuyển một điện tích thửq doc theo cung \( M N \) của vòng tròn đó thì công của lực điện sẽ bằng bao nhiêu?

Ở đây, ta hiểu độ giảm thế năng là hiệu giữa giá trị của thế năng ở điểm đầu và giá trị của thế năng ở điểm cuối. Độ giảm thế năng là một đại lượng đại số.

C3 Thế năng của điện tích thử \( q \) trong điện trường của điện tích điểm \( Q \) nêu ở C2 sẽ thay đổi thế nào khi \( q \) di chuyển dọc theo cung \( M N \) ?

Tương tự như thế năng của một vật trong trọng trường, thế năng của một điện tích q trong điện truoòng đạc tru’ng cho khả năng sinh công của điện tru’òng khi đặt điện tích q tại điểm mà ta xét trong diện truiơng.

Ta sẽ lấy số đo thế năng của điện tích trong điện trường là công mà điện trường có thể sinh ra khi cho điện tích di chuyển từ điểm mà ta xét đến điểm mốc để tính thế năng. Điểm mốc thường được coi là điểm mà lực điện hết khả năng sinh công .

Đối với một điện tích \( q \) (dương) đặt tại điểm \( M \) trong điện trường dều thì công này là :

\[

A=q E d=W_{\mathrm{M}}

\]

trong đó \( d \) là khoảng cách từ điểm \( M \) đến bản âm ; \( W_{\mathrm{M}} \) là thế năng của điện tích \( q \) tại \( M \).

Trong trường hợp điện tích \( q \) nằm tại điểm \( M \) trong một điện trường bất kì do nhiều điện tích gây ra thì có thể lấy thế năng bằng công của lực điện khi di chuyển \( q \) từ \( M \) ra vô cực \( \left(A_{\mathrm{Mos}}\right) \). Đó là vì ở vô cực, tức là ở rất xa các điện tích gây ra điện trường, thì điện trường bằng 0 và lực điện cũng bằng 0 . Do vậy :

\[

W_{\mathrm{M}}=A_{\mathrm{M} \infty}

\]

2. Sự phụ thuộc của thếnăng \( W_{M} \) vào điện tích \( q \)

Vî độ lớn của lực điện luôn tỉ lệ thuận với điện tích thử \( q \) nên công \( A_{\mathrm{M} \omega} \) và do đó, thế năng của điện tích tại \( M \) cũng tỉ lệ thuận với \( q \) :

\[

A_{\mathrm{M} \infty}=W_{\mathrm{M}}=V_{\mathrm{M}} q

\]

\( V_{\mathrm{M}} \) là một hệ số tỉ lệ, không phụ thuộc \( q \) mà chỉ phụ thuộc vị trí điểm \( M \) trong điện trường

3. Công của lực điện và độ giảm thế năng của điện tích trong điện trường

Từ định luật bảo toàn và chuyển hoá năng lượng, ta có thể suy ra kết quả sau đây :

Khi một điện tích q di chuyển tù̀ điểm \( M \) dến điểm \( N \) trong một điện tru'ờng thì công mà lưc điện tác dung lên điện tích đó sinh ra sê bằng dộ giảm thế năng của diện tích q trong diện trưò̀ng. C 3

\[

A_{\mathrm{MN}}=W_{\mathrm{M}}-W_{\mathrm{N}}

\]

Công của lực điện trong sự di chuyển của một điện tích không phụ thuộc hình dạng đường đi mà chỉ phụ thuộc vị trí điểm đẩu và điểm cuối của đường đi trong điện trường.

Thế năng của một điện tích điểm \( q \) tại điểm \( M \) trong điện trường :

\[

W_{M}=A_{M < a}=v_{M} q

\]

Thế năng tỉ lệ thuận với \( q \).

Công của lực điện bằng độ giảm thế năng của điện tích trong điện trường.

CÂU HỎI VÀ BÀI TẬP

1. Viết công thức tính công của lực điện trong sự di chuyển của một điện tích trong một điện trường đều.
2. Nêu đặc điểm của công của lực điện tác dụng lên điện tích thử \( q \) khi cho \( q \) di chuyển trong điện trường.
3. Thế năng của điện tích \( q \) trong một điện trường phụ thuộc vào \( q \) như thế nào?
4. Cho điện túch thử \( q \) di chuyển trong một điện trường đều dọc theo hai đoạn thẳng \( M N \) và \( N P \).

Biết rằng lực điện sinh công dương và \( M N \) dài hơn \( N P \). Hỏ̉i kết quả nào sau đây là đúng, khi so sánh các công \( A_{M N} \) và \( A_{\mathrm{NP}} \) của lực điện ?

1. \( A_{\text {MN }} > A_{\text {NP. }} \).
2. \( A_{\mathrm{MN}} < A_{\mathrm{NP}} \).
3. \( A_{\mathrm{MN}}=A_{\mathrm{NP}} \).
4. Cả ba trường hợp \( A, B, C \) đều có thể xảy ra.
5. Một êlectron di chuyển được đoạn đường 1 cm , dọc theo một đường sức điện, dưới tác dụng của lực điện trong một điện trường đều có cường độ điện trường \( 1000 \mathrm{~V} / \mathrm{m} \). Hỏi công của lực điện có giá trị nào sau đây?
6. \( -1,6 \cdot 10^{-16} \mathrm{~J} \).
7. \( +1,6 \cdot 10^{-16} \mathrm{~J} \).
8. \( -1,6 \cdot 10^{-18} \mathrm{~J} \).
9. \( +1,6 \cdot 10^{-18} \mathrm{~J} \).
10. Cho một điện tích di chuyển trong điện trường dọc theo một đường cong kín, xuất phát từ điểm \( M \) rổi trở lại điểm \( M \). Công của lực điện bằng bao nhiêu?
11. Một êlectron được thả không vận tốc ban đầu ở sát bản âm, trong điện trường đều giữa hai bản kim loại phẳng, tích điện trái dấu. Cường độ điện trường giữa hai bản là \( 1000 \mathrm{~V} / \mathrm{m} \). Khoảng cách giữa hai bản là 1 cm .

Tính động năng của êlectron khi nó đến đập vào bản dương.

12. Cho một điện tích dương \( Q \) đặt tại điểm \( O \). Đặt một điện tích âm \( q \) tai điểm \( M \). Chứng minh rằng thế năng của \( q \) ở \( M \) có giá trị âm.