(Trang 62)
SAU BÀI HỌC NÀY EM SẼ:
- Sử dụng được các hàm tính các đặc trưng đo xu thế trung tâm: trung bình cộng (mean), trung vị (median), mốt (mode), tứ phân vị (quartile).
- Sử dụng được các hàm tính các đặc trưng về đo độ phân tán: khoảng biến thiên và phương sai, độ lệch chuẩn, hệ số biến thiên.
Em đã biết công thức tính các thống kê cơ bản cho một số liệu mẫu trên Excel trong chương trình Toán lớp 10 và 11. Hãy tính một vài giá trị đặc trưng cho dãy số liệu: 2, 4, 2, 6, 4, 5, 1, 0, 3, 5, 7.
1. MÔ TẢ DỮ LIỆU THỐNG KÊ TRONG EXCEL
a) Tìm hiểu về dữ liệu thống kê
Hoạt động Tìm hiểu về dữ liệu thống kê
Hình 11.1 là một phần kết quả tuyển sinh của trường đại học K. Những cột dữ liệu nào trong bảng dữ liệu đó là dữ liệu thống kê? Các dữ liệu đó thuộc loại dữ liệu thống kê nào?
Các cột từ A đến H ở Hình 11.1 đều là dữ liệu thống kê. Dữ liệu thống kê có hai loại chính:
- Dữ liệu định lượng: Loại dữ liệu đo lường được, thường là số. Ví dụ: chiều cao, trọng lượng, điểm số,... Các cột E đến H trong Hình 11.1 là các dữ liệu định lượng.
- Dữ liệu định tính: Loại dữ liệu mô tả tính chất hoặc loại, thường là các nhóm hoặc định danh. Ví dụ: màu sắc, giới tính,... Các cột A đến D trong Hình 11.1 là các dữ liệu định tính.
Mô tả dữ liệu thống kê là một trong ba bài toán đơn giản của phân tích dữ liệu thống kê: mô tả dữ liệu, phân tích tương quan và kiểm định giả thuyết. Mô tả dữ liệu thống kê gồm nhiều nội dung khác nhau, trong bài này sẽ chỉ đề cập việc xác định đặc trưng đo xu thế trung tâm và độ phân tán của các dãy số.
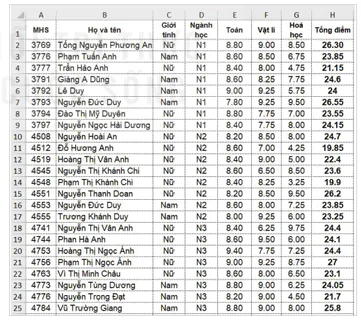
Hình 11.1. Dữ liệu sinh viên trúng tuyển khối A00
(Trang 63)
b) Một số đặc trưng đo xu thế trung tâm
Trong môn Toán, em đã được tìm hiểu về các đặc trưng đo xu thế trung tâm: trung bình cộng (mean), trung vị (median), tứ phân vị (quartile), mốt (mode). Các đặc trưng trung tâm giúp tóm tắt và mô tả xu thế trung tâm của dãy số, giúp hiểu rõ hơn về sự phân phối và tính chất của dãy số. Tuy nhiên, việc sử dụng đặc trưng nào cho phù hợp với tính chất của dãy số và mục tiêu của phân tích là việc cần được cân nhắc. Chẳng hạn một kì thi sát hạch có 10 câu trắc nghiệm mỗi câu 1 điểm. Bảng 11.1 là kết quả của 3 ca thi khác nhau, cho biết số thí sinh đạt được mức điểm thi tương ứng từ 0 tới 10.
| Điểm số | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Số thí sinh | Ca 1 | 1 | 2 | 4 | 7 | 10 | 12 | 10 | 7 | 4 | 2 | 1 |
| Ca 2 | 1 | 2 | 3 | 5 | 9 | 10 | 11 | 8 | 6 | 4 | 1 | |
| Ca 3 | 0 | 4 | 6 | 11 | 10 | 9 | 7 | 5 | 4 | 3 | 1 | |
Bảng 11.1. Kết quả thi trắc nghiệm
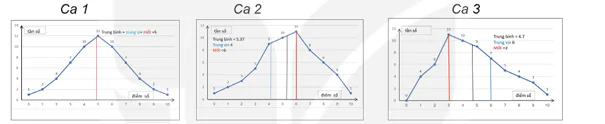
Từ bảng trên ta có biểu đồ phân phối của tần số các điểm thi các ca thi như sau:
Ca 1
Ca 2
Ca 3
Hình 11.2. Biểu đồ phân phối của tần số điểm thi
Trong các biểu đồ mỗi chấm tròn biểu diễn một cặp toạ độ (mức điểm, số thí sinh đạt mức điểm đó). Đỉnh của biểu đồ xác định tại giá trị điểm có số thí sinh nhất nhiều (Mốt). Chẳng hạn, Ca 1 có đỉnh biểu đồ tại mức điểm bằng 5 và số thí sinh đạt điểm 5 là 12, Ca 2 có đỉnh biểu đồ tại mức điểm bằng 7 và số thí sinh đạt 7 điểm là 11,...
Ca 1: Biểu đồ tần số các điểm thi đối xứng: Số dấu chấm tròn hai phía của Đỉnh bằng nhau (cùng là 5). Trong trường hợp này trung bình, trung vị, mốt bằng nhau.
Ca 2: Biểu đồ tần số các điểm thi lệch trái: Số dấu chấm tròn bên trái Đỉnh nhiều hơn bên phải (6 so với 4). Trong trường hợp này, trung vị < trung bình < mốt.
Ca 3: Biểu đồ tần số các điểm thi lệch phải: Số dấu chấm tròn bên trái Đỉnh ít hơn bên phải (3 so với 7). Trong trường hợp này, trung vị > trung bình > mốt.
Trong mỗi trường hợp như trên, có thể chọn số đo xu thế trung tâm khác nhau làm đại diện cho trung tâm dãy số.
Nói chung, khi dữ liệu có phân phối lệch, việc lựa chọn giá trị trung vị làm đặc trưng xu thế trung tâm của dãy số sẽ phù hợp hơn so với giá trị trung bình. Excel cung cấp các hàm tương ứng giúp dễ dàng xác định các đặc trưng đo xu thế trung tâm nói trên.
- Hàm AVERAGE được sử dụng để tính trung bình của dãy số.
Cú pháp: AVERAGE(number1, [number2],...), trong đó: number1, [number2],... là số hoặc vùng ô chứa số.
Ví dụ: TRUNG BÌNH (10, A1:B4), TRUNG BÌNH(RAND(), A1:B4), ...
(Trang 64)
- Hàm MEDIAN được sử dụng để tính giá trị trung vị của dãy số liệu.
Cú pháp: MEDIAN(number1, [number2],...), trong đó: number1, [number2],... là số hoặc vùng ô chứa số.
Hàm MODE được dùng để tìm giá trị có số lần xuất hiện lớn nhất của dãy số liệu.
Cú pháp: MODE(number1, [number2],...), trong đó: number1, [number2],... là số hoặc vùng ô chứa số.
Lưu ý: Mốt có thể dùng đối với biến định tính được mã hoá bằng số.
Khi dãy số có nhiều giá trị mốt, hàm MODE trả về giá trị mốt xuất hiện đầu tiên trong dãy số. Nếu muốn biết tất cả các giá trị mốt thì em có thể dùng hàm MOD.MULT (với Excel phiên bản từ 2010).
- Hàm QUARTILE.INC được sử dụng để tìm các giá trị nhỏ nhất, lớn nhất hoặc các tứ phân vị của dãy số.
Cú pháp: QUARTILE.INC (array, quart), trong đó:
- array là mảng số liệu hoặc vùng dữ liệu số.
- quart bằng 0, 1, 2, 3, 4 tương ứng với giá trị hàm là MIN, Q1, Q2, Q3, MAX.
Các giá trị tứ phân vị Q1, Q2, Q3 là các giá trị chia dãy số thành bốn khoảng có số lượng số bằng nhau theo chiều tăng dần, tức là 25% số giá trị không lớn hơn Q1, 50% số giá trị không lớn hơn Q2 và 75% số giá trị không lớn hơn Q3.
c) Các đặc trưng đo độ phân tán
Các đặc trưng đo độ phân tán thường được sử dụng bao gồm phương sai, độ lệch chuẩn, hệ số biến thiên, và khoảng biến thiên. Các đặc trưng đo độ phân tán giúp mô tả sự biến động và phân tán của dãy số, cung cấp cái nhìn toàn diện về đặc tính phân phối và biến động của tập hợp dữ liệu. Việc kết hợp các đặc trưng này thường được sử dụng để đánh giá và so sánh sự biến động giữa các dãy số khác nhau. Excel cung cấp các hàm giúp dễ dàng tính các đặc trưng này.
- Hàm VAR được sử dụng để tính phương sai của dãy số.
Cú pháp: VAR(number1, [number2],...), trong đó:
number1, [number2],... là số hoặc vùng ô chứa số.
- Hàm STDEV được sử dụng giá trị độ lệch chuẩn của dãy số.
Cú pháp: STDEV(number1, [number2]....), trong đó:
number1, [number2],... là số hoặc vùng ô chứa số.
Trong thực tế, do có cùng đơn vị với số liệu nên độ lệch chuẩn thường được dùng nhiều hơn phương sai.
- Hệ số biến thiên: Được xác định bằng cách tính tỉ lệ (%) của độ lệch chuẩn (sửdụng hàm STDEV) và trung bình cộng (sử dụng hàm AVERAGE).
- Khoảng biến thiên: Được xác định bằng hiệu của giá trị lớn nhất (sử dụng hàm MAX) và giá trị nhỏ nhất (sử dụng hàm MIN) của dãy số.
Excel có hàm tính các số đặc trưng đo xu thế trung tâm như AVERAGE, MEDIAN, MODE, QUARTILE.INC; các hàm tính các số đo độ phân tán của dữ liệu thống kê như VAR, STDEV. VAR và STDEV đo độ phân tán xung quanh giá trị trung bình.
1. Cho dãy số: 1, 3, 6, 4, 6, 7, 3, 4, 4, 5, 9, 16,4, 2, 8. Em dùng đặc trưng nào sau đây để mô tả trung tâm của dãy số này?
A. Trung bình
B. Trung vị
C. Mốt
D. Khoảng biến thiên
(Trang 65)
2. Cho dãy số về chiều cao (cm) của nam 18 tuổi: 168, 173,176, 175, 162, 180, 170, 173, 166. Em dùng hàm nào sau đây để tính độ phân tán của dãy số này?
A. AVERAGE
B. QUARTILE
C. STDEV
D. MEDIAN
3. Cho kết quả khảo sát về màu áo ấm mùa đông ưa thích của nữ sinh (với mã các màu là 1: Đen, 2: Hồng, 3: Tím, 4: Màu khác) như sau: 1, 1, 2, 3, 4, 3, 3, 1, 4, 4, 2, 2, 3, 1, 1, 2, 1, 1.
Em dùng hàm nào sau đây để tìm màu áo ấm mùa đông nhiều nữ sinh ưa thích nhất?
A. AVERAGE
B. MEDIAN
C. MODE
D. VAR
2. THỰC HÀNH MÔ TẢ DỮ LIỆU
Nhiệm vụ 1: Lựa chọn số đặc trưng xu thế trung tâm của các dãy số
Yêu cầu: Với số liệu ở Hình 11.1, em sẽ chọn trung bình, trung vị hay mốt làm giá trị trung tâm của điểm từng môn Toán, Vật lí, Hoá học? Từ đó rút ra một vài nhận xét có ý nghĩa.
Hướng dẫn:
Bước 1. Mở trang tính với dữ liệu Hình 11.1 (vùng dữ liệu A1:H25). Nhập các tiêu đề Các số đặc trưng trung tâm, Trung bình, Trung vị, Mốt vào các ô B27:B30; nhập các tiêu đề Toán, Vật lí, Hoá học vào các ô C27:E27 (Hình 11.3).
Bước 2. Tính các số đặc trưng tương ứng bằng các hàm trong Excel
- Nhập = AVERAGE(E2:E25) vào ô C28 để tính giá trị trung bình.
- Nhập lần lượt các công thức =MEDIAN(E2:E25); =MODE(E2:E25) vào các ô C29, C30.
Sao chép các ô C28:C30 vào các ô D28:E30 và E28:E30. Kết quả nhận được như Hình 11.3.

Hình 11.3. Kết quả tính các đặc trưng trung tâm
Nhận xét: Điểm Toán có các giá trị trung bình, trung vị, mốt xấp xỉ nhau, có thể xem trung bình là đại diện đo xu thế trung tâm. Điểm Vật lí có mốt và trung vị cao hơn, có 5/24 sinh viên đạt điểm 9 môn này trong khi điểm trung bình là 8.35, tính đại diện của trung bình thấp nên có thể chọn mốt là đặc trưng trung tâm. Môn Hoá học có giá trị trung bình 6.95 và trung vị 7.13 khác nhau không đáng kể, tuy nhiên có 10/24 sinh viên điểm thấp hơn trung bình và có 12/24 sinh viên có điểm thấp hơn trung vị. Do vậy, với môn Hoá học, chọn trung vị làm giá trị đo xu thế trung tâm cho điểm môn này sẽ hợp lí hơn.
Nhiệm vụ 2: Phân tích tứ phân vị
Yêu cầu: Giả sử trong số trúng tuyển khối A00 (Hình 11.1) sẽ có 50% sinh viên điểm cao nhất được giảm học phí năm thứ nhất, trong đó một nửa cao hơn được giảm 20% và nửa thấp hơn được giảm 10%. Hãy cho biết các sinh viên Đào Thị Mỹ Duyên, Phan Hà Anh và Tống Nguyễn Phương An có được giảm học phí không và được giảm ở mức nào?
(Trang 66)
Hướng dẫn:
Bước 1. Phân tích bài toán: Những sinh viên có Tổng điểm từ Q3 trở lên thuộc nhóm 25% sinh viên có Tổng điểm cao nhất. Tương tự, những sinh viên có Tổng điểm từ Q2 (trung vị của Tổng điểm) trở lên thuộc nhóm 50% sinh viên có Tổng điểm cao nhất. Cần so sánh Tổng điểm của mỗi học sinh với Q2 và Q3 để có câu trả lời.
Bước 2. Tính Q2 và Q3
Nhập các tiêu đề Tứ phân vị, Q3, Q2 vào các ô A30:A32; nhập các tiêu đề quart, Tổng điểm vào các ô B30:C30 và nhập các số 3, 2 vào các ô B31:B32 như Hình 11.4. Nhập công thức =QUARTILE.INC(H2:H25, B31) vào ô C31, nhấn Enter. Sao chép ô C31 vào ô C32. Kết quả như Hình 11.4.
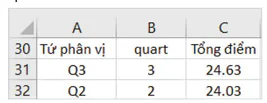
Hình 11.4. Tìm tứ phân vị Q3 và Q2 của Tổng điểm
Nhận xét: Theo kết quả tính được trong Hình 11.3, Đào Thị Mỹ Duyên không được giảm học phí, Phan Hà Anh được giảm 10% và Tống Nguyễn Phương An được giảm 20% học phí năm học thứ nhất.
Nhiệm vụ 3: Phân tích kết hợp trung bình và độ phân tán
Yêu cầu: Hãy tính số đo đặc trưng trung bình và độ phân tán của điểm các môn thi THPT các môn trong Hình 11.1 và nêu một vài nhận xét từ kết quả thu được.
Hướng dẫn:
Bước 1. Mở trang tính với dữ liệu Hình 11.1 (vùng dữ liệu A1:H25). Tạo nhãn cho các môn Toán, Vật lí, Hoá học và Tổng điểm vào các ô M1:P1 và các đặc trưng Trung bình, Phương sai; Độ lệch chuẩn, Khoảng biến thiên, Hệ số biến thiên vào các ô L2: L6 (Hình11.5).
Bước 2. Tính các đặc trưng.
Nhập công thức =AVERAGE (E2:E25) vào ô M2, nhấn Enter.
Nhập công thức = VAR(E2:E25) vào ô M3, nhấn Enter.
Nhập công thức =STDEV (E2:E25) vào ô M4, nhấn Enter.
Nhập công thức =MAX(E2:E25)- MIN(E2:E25) vào ô M5, nhấn Enter.
Nhập công thức =M4/M2*100 vào ô M6, nhấn Enter.
Sao chép các ô (M2:M6) vào các ô (N2:P6).
Kết quả tính được như Hình 11.5.
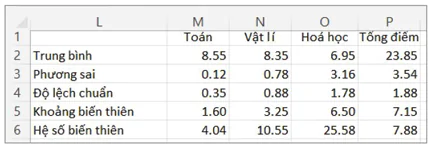
Hình 11.5. Giá trị đặc trưng trung bình và độ phân tán
(Trang 67)
Nhận xét: Kết quả tính toán cho thấy điểm trung bình Toán cao, kết quả đồng đều (ổn định) hơn do các đặc trưng phân tán đều nhỏ nhất so với hai môn còn lại. Các môn khác điểm trung bình thấp hơn nhưng biến động nhiều hơn, nhất là điểm Hoá học. Như vậy đóng góp của điểm Toán vào Tổng điểm nhiều nhất và ổn định nhất, điểm Hoá học đóng góp vào Tổng điểm thấp nhất và phân tán nhất. Nếu chỉ so sánh Khoảng biến thiên thì mức biến động điểm môn Vật lí gấp hai lần và môn Hoá học gấp bốn lần so với môn Toán. Tuy nhiên nếu so sánh kết hợp thêm Hệ số biến thiên thì có thể thấy mức độ phân tán của điểm môn Vật lí gấp 2.5 lần và môn Hoá học gấp 6 lần so với môn Toán. Nếu chỉ xem xét các giá trị Trung bình, Phương sai, Độ lệch chuẩn, Khoảng biến thiên giữa điểm môn Hoá học và Tổng điểm, có thể thấy môn Hoá học đóng góp gần 1/3 số điểm vào Tổng điểm, các đặc trưng khác đều tương đương. Điều này dễ dẫn tới ngộ nhận về vai trò điểm môn Hoá học trong kết quả xét tuyển. Tuy nhiên, nếu xét thêm Hệ số biến thiên, rõ ràng môn Hoá học có mức độ biến động điểm lớn hơn ba lần so với Tổng điểm, nghĩa là mức độ đóng góp của điểm môn Hoá học vào Tổng điểm xét tuyển không ổn định khi xem xét tổng thể danh sách trúng tuyển ở Hình 11.1.
Những nhận xét nêu trên cho thấy việc xem xét kết hợp các giá trị đặc trưng có thể cho cái nhìn đầy đủ hơn về tập số liệu thống kê. Đây cũng là điều mà các nhà phân tích thống kê trong thực tế thường làm.
LUYỆN TẬP
1. Sử dụng số liệu Hình 11.1 trả lời các câu hỏi sau:
a) Điểm Hoá học thấp nhất của 25% sinh viên có điểm Hoá học cao nhất là bao nhiêu?
b) Điểm môn nào có khoảng biến thiên lớn nhất?
2. Cho dữ liệu nhiệt độ cao nhất trong 30 ngày tháng 4 năm 2023 tại Thành phố A.
| 32.8 | 33.6 | 31.6 | 36.5 | 34.7 | 31.0 | 33.1 | 32.3 | 33.6 | 32.7 |
| 31.3 | 32.0 | 36.6 | 31.9 | 34.9 | 33.6 | 33.9 | 31.0 | 34.4 | 31.9 |
| 35.5 | 34.9 | 35.4 | 35.4 | 30.3 | 32.1 | 36.1 | 33.0 | 34.4 | 32.6 |
a) Hãy chọn một hàm trong Excel để tìm độ phân tán của dữ liệu này.
b) Hãy tìm nhiệt độ thấp nhất trong 75% số ngày nhiệt độ cao nhất.
VẬN DỤNG
1. Cho dãy số: 1, 4, 5, 14, 6, 5, 1, 4, 5, 4, 7, 2, 5, 3, 2. Em hãy tính trung bình và trung vị bằng các hàm trong Excel theo hai cách và nhận xét các kết quả.
a) Tính cho dãy số hiện có.
b) Tính sau khi thay số 14 bằng trung bình của dãy số hiện có.
2. Em có thể tính giá trị trung bình của hai vùng số liệu điểm Toán của 7 sinh viên đầu tiên và 5 sinh viên cuối cùng trong dữ liệu Hình 11.1 hay không?
3. Điểm Hoá học của 75% sinh viên trong dữ liệu Hình 11.1 xếp theo chiều tăng dần không cao hơn bao nhiêu?

































































Bình Luận
Để Lại Bình Luận Của Bạn