Nội Dung Chính
(Trang 85)
SAU BÀI HỌC NÀY EM SẼ:
- Biết sơ bộ một số khái niệm liên quan đến bài toán kiểm định giả thuyết thống kê.
- Giải quyết được bài toán kiểm định giả thuyết đơn giản: về giá trị tham số trung bình của một biến ngẫu nhiên và sự khác nhau của hai trung bình của hai biến ngẫu nhiên nhờ các hàm kiểm định trong Excel.
- Biết cách vận dụng các kiểm định này vào một số nhiệm vụ cụ thể.
Giả sử, trong những nghiên cứu thống kê trước đây với quy mô cả nước, người ta đã tính được chỉ số thông minh (IQ) trung bình của học sinh lớp 12 là 100. Năm nay, khảo sát ngẫu nhiên chỉ số này của 100 học sinh lớp 12 và từ số liệu khảo sát tính được trung bình IQ là 110. Liệu chỉ số IQ trung bình của học sinh lớp 12 có tăng lên so với trước? Phương pháp thống kê nào trả lời được câu hỏi này?
1. BÀI TOÁN KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
a) Khái niệm bài toán kiểm định và giả thuyết thống kê
Để giải quyết các câu hỏi như trong phần khởi động, người ta có thể sử dụng phương pháp kiểm định giả thuyết thống kê.
Giả thuyết thống kê là một phát biểu (một tuyên bố) về tổng thể (hay quần thể). Kiểm định giả thuyết thống kê là một phương pháp sử dụng các kĩ thuật thống kê để đưa ra quyết định về việc bác bỏ hay không bác bỏ một giả thuyết thống kê trên cơ sở dữ liệu mẫu quan sát từ tổng thể.
Có nhiều bài toán kiểm định giả thuyết thống kê nhưng trong bài này ta chỉ tìm hiểu hai bài toán kiểm định tham số trung bình sau đây:
- Kiểm định tham số trung bình (µ) của tổng thể (kiểm định một giá trị trung bình).
- So sánh (kiểm định) hai giá trị trung bình (µ₁) và (µ₂) của hai tổng thể phân phối chuẩn.
Mỗi bài toán kiểm định luôn có hai giả thuyết cần xác định: giả thuyết gốc kí hiệu là H, và giả thuyết thay thế kí hiệu là H,.
Với hai bài toán được xem xét trong bài này, các giả thuyết Ho và H, được phát biểu như sau.
- Bài toán kiểm định một giá trị trung bình
Hoạt động 1 Xác định các giả thuyết của bài toán kiểm định một giá trị trung bình
Hãy cùng thảo luận và xác định giả thuyết gốc Họ, giả thuyết thay thế H, của bài toán nêu trong phần khởi động.
Bài toán kiểm định một trung bình lựa chọn các giả thuyết như sau:
- Giả thuyết gốc H0: µ = µ0 "Giá trị trung bình (µ) của tổng thể bằng µ, cho trước". Giá trị µ thường được xác định trước từ thông tin ngoài dữ liệu quan sát. Chẳng hạn
(Trang 86)
với tình huống nêu trong phần khởi động, µ là giá trị IQ trung bình của học sinh lớp 12 cả nước năm nay (năm quan sát) mà chúng ta chưa biết và có thể cho rằng giá trị này bằng IQ trung bình của học sinh lớp 12 các năm trước, μ0 = 100. Giả thuyết gốc H0 có 0 thể viết ngắn gọn là Họ: μ = 100.
- Giả thuyết thay thế H₁: "Giá trị µ nhỏ hơn hoặc lớn hơn µ0 (kiểm định một phía) hoặc “Giá trị µ khác µ0” (kiểm định hai phía). Trường hợp kiểm định một phía có thể viết gọn là H₁: μ > µ0 hoặc H₁: μ < μ0 Mọi với trường hợp kiểm định hai phía H₁: μ ≠ μο
- Giả thuyết thay thế H, nói chung là một trong các giả thuyết khác giả thuyết gốc. Giả thuyết này có thể phát sinh từ dữ liệu hay các thông tin khác. Chẳng hạn, với tình huống nêu trong phần khởi động, giả thiết thay thế là H₁: μ > μο (hay μ > 100), vì theo số liệu quan sát IQ của 100 học sinh ta có trung bình mẫu số liệu là 110 (lớn hơn 100).
- Bài toán kiểm định hai giá trị trung bình
Hoạt động 2
Trọng lượng của trẻ 36 tháng tuổi là đại lượng ngẫu nhiên phân phối chuẩn. Do các điều kiện khác nhau ở hai thành phố A và B, người ta muốn so sánh khối lượng trung bình của trẻ 36 tháng tuổi ở hai thành phố này. Gọi µ₁, µ₂ là khối lượng trung bình của trẻ độ tuổi này ở hai thành phố A và B. Em hãy chọn giả thuyết gốc và giả thuyết thay thế để kết luận về vấn đề trên trong trường hợp:
a) Chưa có số liệu về khối lượng của trẻ 36 tháng tuổi ở các thành phố A và B.
b) Có số liệu thu thập về khối lượng của các trẻ độ tuổi này của 50 trẻ ở mỗi thành phố trên và tính được khối lượng trung bình của 50 trẻ ở thành phố A là 14.2 kg, 50 trẻ ở thành phố B là 14.5 kg.
Bài toán kiểm định hai trung bình lựa chọn các giả thuyết như sau: Bài
- Giả thuyết gốc Họ: μ₁= μί
- Giả thuyết thay thế H₁: µ₁> µ₂ hoặc H₁: µ₁ < µ₂ (kiểm định một phía);
hoặc H₁: μ₁ ≠ µ₂ (kiểm định hai phía).
Chẳng hạn, với bài toán trong Hoạt động 2, sử dụng bài toán kiểm định giả thuyết về hai trung bình trong hai trường hợp:
Trường hợp a: Chúng ta không biết được điều kiện chăm sóc trẻ ở hai thành phố ảnh hưởng đến khối lượng của trẻ như thế nào. Vì vậy, giả thuyết gốc sẽ chọn là Họ: μ₁ = μ₂. Giả thuyết thay thế, khi không có cơ sở để cảm nhận trẻ ở thành phố A hay B có khối lượng lớn hơn, sẽ là H₁: μ, ≠ μ₂. Đây là bài toán kiểm định hai phía.
Trường hợp b: Chúng ta có thông tin từ số liệu mẫu ở các thành phố A và B. Đó là cơ sở chọn H₁: μ₁ < μ₂. Đây là bài toán kiểm định một phía.
b) Kết luận của bài toán kiểm định tham số và các sai lầm có thể
Bài toán kiểm định thống kê luôn có một trong hai kết quả:
- Bác bỏ Ho, chấp nhận H₁.
- Không đủ cơ sở bác bỏ Ho (hay không bác bỏ H₂), không chấp nhận H₁.
Các sai lầm có thể xảy ra trong các kết luận: Kết luận của kiểm định nói riêng không thể đúng hoàn toàn (100%). Các sai lầm (rủi ro) có thể là:
- Sai lầm loại 1: Bác bỏ Ho khi Ho đúng. Xác suất mắc sai lầm này kí hiệu là a.
- Sai lầm loại 2: Không bác bỏ Ho khi Ho sai.
(Trang 87)
Trong một bài toán kiểm định với một bộ số liệu, nếu muốn giảm sai lầm này thì sẽ làm tăng sai lầm kia. Vì vậy người ta chọn cách chấp nhận mức sai lầm loại 1, với a đủ nhỏ cho trước (thường chọn a = 0.05 hoặc 0.01). Giá trị a được gọi là mức ý nghĩa của kiểm định.
c) Các hàm trong Excel giải quyết các bài toán kiểm định trung bình
- Hàm Z.TEST: Hàm Z.TEST thuộc nhóm hàm thống kê (Statistical), được sửdụng để kiểm định giả thuyết về một giá trị trung bình của một tổng thể, còn gọi là kiểm định một mẫu.
Cú pháp: Z.TEST(array, x, [sigma]), trong đó:
- array: mảng dữ liệu mẫu của biến X.
- x: giá trị kiểm định giả thuyết trung bình của X (µ = x).
- sigma: độ lệch chuẩn của X, trường hợp bỏ trống Excel dùng độ lệch chuẩn mẫu.
Sử dụng giá trị hàm Z.TEST: đặt P = MIN(Z.TEST, 1- Z.TEST). Với mức ý nghĩa a, ta có thể đưa ra kết luận theo Bảng 15.1.
Bảng 15.1. Kết luận của kiểm định giả thuyết với mức ý nghĩa a
| Giả thuyết H₁ | μ≠μο | μ > μο | μ < μο |
| Điều kiện bác bỏ H | 2P ≤ α | Mean (X) > µo và P ≤ a | Mean (X) < μo và P≤ a |
- Hàm T.TEST: Hàm T.TEST cùng nhóm với hàm Z.TEST, được dùng để so sánh hai giá trị trung bình (mean) của hai biến X₁, X2. Hàm T.TEST sử dụng để kiểm định giả thuyết gốc Ho - hai trung bình bằng nhau với các giả thuyết thay thế H₁ - hai trung bình khác nhau hoặc trung bình X₁ lớn/nhỏ hơn trung bình X₂. Kiểm định này dựa trên số liệu mẫu của hai biến X₁ và X₂, vì vậy thường gọi là kiểm định hai mẫu.
Cú pháp: T.TEST(array1, array2, Tails, Type), trong đó:
- array1: mảng dữ liệu mẫu của biến X₁; array2: mảng dữ liệu mẫu của biến X2. Thứ tự khai báo hai vùng không ảnh hưởng đến giá trị của hàm.
- Tails: 1: Kiểm định một phía; 2: Kiểm định hai phía.
- Type: 1: Số liệu quan sát theo cặp; 2: Giả thiết phương sai bằng nhau; 3: Không giả thiết phương sai bằng nhau.
Sử dụng giá trị hàm T.TEST, với mức ý nghĩa a, ta có thể đưa ra kết luận theo Bảng 15.2.
Bảng 15.2. Kết luận của kiểm định giả thuyết với mức ý nghĩa α
| Giả thuyết H₁ | μ ≠ μ₂ | μ₁ > μ2 | μ<μ₂ |
| Điều kiện bác bỏ Ho | T.TEST ≤ α | Mean(X₁) > Mean(X2) và T.TEST <α | Mean(X₁) < Mean(X2) và T.TEST ≤ α |
Lưu ý:
Với một bài toán cụ thể, nếu các điều kiện bác bỏ H trong các Bảng 15.1 hoặc Bảng 15.2 không thoả mãn, người ta kết luận "không đủ điều kiện chấp nhận H, nhưng cũng không đủ điều kiện bác bỏ Ho".
1. Em sẽ chọn giả thuyết đối nào cho kiểm định 1 phía với Họ: μ = µ khi trung bình số liệu mẫu lớn hơn µ?
2. Khi kiểm định giả thuyết 1 trung bình bằng Z.TEST, giá trị trả về của hàm Z.TEST là 0.04. Với mức ý nghĩa 5%, em có bác bỏ giả thuyết gốc hay không?
(Trang 88)
2. THỰC HÀNH
Phần thực hành này sẽ sử dụng dữ liệu mẫu ở Hình 11.1. Cần lưu ý đây chỉ là một phần nhỏ của dữ liệu sinh viên trúng tuyển các ngành N1, N2, N3 khối A00 của trường K.
Nhiệm vụ 1: Kiểm định giả thuyết về một giá trị trung bình
Nhiệm vụ 1.1: Trung bình Tổng điểm trúng tuyển khối A00 của trường K là 23 điểm. Trung bình Tổng điểm trúng tuyển của sinh viên ba ngành này cao hơn trung bình Tổng điểm trúng tuyển khối A00 của trường K, đúng hay sai? Kết luận với mức ý nghĩa 5%.
Hướng dẫn:
Bước 1. Phân tích bài toán:
- Em biết trung bình của Tổng điểm trúng tuyển khối A00 của trường K là 23 và thông tin Tổng điểm của 24 sinh viên trúng tuyển khối A00 ở Hình 11.1. Với yêu cầu nhiệm vụ trên em cần thực hiện kiểm định 1 trung bình (µ) của biến X: điểm trung bình trúng tuyển vào các ngành N1, N2, N3 khối A00 của trường K.
- Câu hỏi liệu trung bình điểm trúng tuyển 3 ngành trên bằng hay cao hơn điểm trúng tuyển trung bình khối A00, trường K (là 23 điểm). Các giả thuyết cần chọn như sau: Giả thuyết gốc: H: µ = 23 (trung bình điểm trúng tuyển 3 ngành trên bằng trung bình khối A00 của trường K). Giả thuyết đối H₁: μ > 23 (trung bình điểm trúng tuyển 3 ngành trên cao hơn trung bình điểm trúng tuyển khối A00 của trường K).
- Sử dụng hàm Z.TEST để tìm câu trả lời với mức ý nghĩa a = 5%.
Bước 2. Chuẩn bị dữ liệu: Nhập nhãn cho các ô (12:15) và (K3:K4) và các tham số vào các ô (J2:J5) như Hình 15.1.
Bước 3. Thực hiện các tính toán
Nhập công thức=AVERAGE(H2:H25) vào ô J5, được kết quả ở ô J5 là 23.9.
Nhập công thức =Z.TEST(H2:H25 J3) vào ô L3, được kết quả ở ô L3 là 0.013.

Hình 15.1. Trang dữ liệu
Nhập công thức =MIN(L3, 1-L3) vào ô L4, được kết quả ở ô L4 là 0.013.

=Z.TEST(H2:H25, K3)
= MIN(L3, 1-L3)
=AVERAGE(H2:H25)
Hình 15.2. Kết quả tính toán
Kết luận: Với kết quả trong Hình 15.2, so sánh giá trị ô L4 = 0.013 với giá trị ô J4 (0.05), kết luận bác bỏ Ho - Chấp nhận H₁, tức là với mức ý nghĩa 5% có thể xác nhận trung bình điểm trúng tuyển của các ngành này ở trường K đã cao hơn trung bình Tổng điểm trúng tuyển của trường K.
Nhiệm vụ 1.2: Trung bình điểm Vật lí của sinh viên trúng tuyển khối A00 của trường K là 8.15. Trung bình điểm Vật lí của sinh viên trúng tuyển trong các ngành N1, N2, N3 có khác mức này không? Kết luận với mức ý nghĩa 5%.
(Trang 89)
Hướng dẫn
Bước 1. Phân tích bài toán: Cần kiểm định giá trị trung bình điểm Vật lí bằng kiểm định hai phía vì câu hỏi cần trả lời là “Trung bình điểm Vật lí của sinh viên trúng tuyển trong các ngành N1, N2, N3 có khác 8.15 không?”. Các giả thuyết cần chọn như sau: Chọn Họ: Giả thuyết H0: μ = 8.15 (trung bình điểm Vật lí của sinh viên trúng tuyển các ngành trên bằng trung bình điểm Vật lí của sinh viên trúng tuyển khối A00, trường K). Chọn H₁: Theo yêu cầu bài toán chọn giả thuyết H₁: µ ≠8.15.
Đây là bài toán kiểm định hai phía cho 1 trung bình. Em có thể sử dụng hàm Z.TEST để tìm câu trả lời với mức ý nghĩa a = 5%.
Bước 2. Chuẩn bị dữ liệu:
Nhập nhãn và dữ liệu vào các ô J2:14; K3:K4 như Hình 15.3.

Hình 15.3. Trang dữ liệu
Hình 15.4. Trang tính toán
Bước 3. Thực hiện các tính toán
Nhập công thức =Z. TEST (F2:F25, K3) vào ô L3. Giá trị Z.TEST là 0.128.
Nhập công thức = MIN(L3, 1-L3) vào ô L4. Giá trị P là 0.128.
Kết quả nhận được như Hình 15.4
Kết luận: Với kết quả trong Hình 15.4, giá trị 2P = 0.256 > 0.05, kết luận không bác bỏ Ho, tức là với mức ý nghĩa 5% không thể xác nhận trung bình điểm Vật lí của sinh viên trúng tuyển viên các ngành N1, N2, N3 khác 8.15.
Nhiệm vụ 2: Kiểm định hai giá trị trung bình – Dùng hàm T.TEST
Nhiệm vụ 2.1: Trong Bài 11 em đã biết với mẫu số liệu gồm 24 sinh viên điểm trung bình môn Toán là 8.55 và môn Vật lí là 8.35. Với mức ý nghĩa 5%, sinh viên ba ngành học này ở trường K có điểm trung bình môn Toán cao hơn điểm trung bình môn Vật lí, đúng hay sai?
Hướng dẫn:
Bước 1. Phân tích bài toán: Cần thực hiện bài toán kiểm định một phía (Tails=1) đối với hai trung bình, mẫu quan sát dạng số liệu cặp, không có giả thuyết phương sai bằng nhau (Type=1).
- Kí hiệu điểm Toán là X₁, điểm Vật lí là X₂, với các trung bình là µ, và µ₂. Theo yêu cầu trên, em cần chọn các giả thuyết: Họ: μ₁ = µ₂ (Trung bình điểm Toán bằng trung bình điểm Vật li) và H₁: μ₁ > µ₂ (Trung bình điểm Toán cao hơn trung bình điểm Vật li).
- Sử dụng hàm T.TEST để giải quyết bài toán và kết luận với mức ý nghĩa a = 5%.
Bước 2. Thực hiện tính toán như trong Hình 15.5.
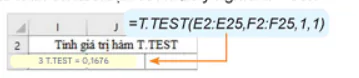
- So sánh với mức ý nghĩa của kiểm định (T.TEST=0.1676 > 0.05), chúng ta kết luận không đủ cơ sở bác bỏ H
J =T.TEST(E2:E25,F2:F25, 1, 1)
Hình 15.5. Giá trị hàm T.TEST
Kết luận: Kết quả trên cho thấy mẫu số liệu có điểm trung bình môn Toán cao hơn Vật lí nhưng không thể kết luận trung bình điểm Toán trong toàn bộ sinh viên trúng tuyển cao hơn điểm trung bình Vật lí.
(Trang 90)
Nhiệm vụ 2.2: Trong mẫu số liệu đang sử dụng có 9 nam và 15 nữ. Trung bình Tổng điểm của Nam và Nữ khác nhau, đúng hay sai? Hãy kết luận với mức ý nghĩa 5%.
Hướng dẫn: Em cần thực hiện bài toán kiểm định hai trung bình với hai mẫu không cùng kích thước.
Bước 1. Phân tích bài toán: Cần thực hiện bài toán kiểm định hai phía (Tail=2) đối với hai trung bình, không có giả thuyết phương sai bằng nhau (Type=3). - Kí hiệu Tổng điểm của nữ là X,, Tổng điểm của nam là X₂, với các trung bình µ, và μ₂. Với yêu cầu trên các giả thuyết cần chọn là: Ho: μ₁ = μ₂ (Hai trung bình bằng nhau) và Η₁: μ, ≠ μ₂ (Hai trung bình khác nhau). Sử dụng hàm T.TEST để giải quyết bài toán và kết luận với mức ý nghĩa 5%. SHA A L D H tinh K C 8.20 5.00 4.50 26.7 Nam 8.00 5.25 6.00 21.25 Nam A 5.00 8.50 6.75 21.45 4953 Nguyễn Đào Duy N $50 8.00 7.25 21.45 A 9.00 5.25 5.75 24 Nam 5.00 6.25 24.05
Bước 2. Tổ chức dữ liệu và tính toán T.TEST
Sắp xếp lại số liệu theo cột Giới tính để được kết quả như Hình 15.6 (các sinh viên nam ở các dòng 2 tới dòng 10, của sinh viên nữ từ dòng 11 đến dòng 25).
Nhập =T.TEST(H2:H10, H11:H25,2,3) vào ô J3. Hàm T.TEST trả về 0.4715 như Hình 15.7.
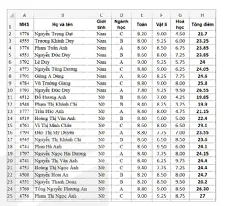
Hình 15.6. Dữ liệu nam, nữ chia thành hai khối
Kết luận: So sánh giá trị này với mức ý nghĩa (T.TEST = 0.4715 > 0.05). Chúng ta kết luận không bác bỏ Ho hay không thể kết luận trung bình Tổng điểm của sinh viên Nam và sinh viên Nữ khác nhau.
LUYỆN TẬP
Hình 15.6 cho số liệu mẫu thu nhập bình quân khẩu/tháng của hai địa phương A và B. Thu nhập bình quân khẩu tháng ở A và B khác nhau, đúng hay sai? Kết luận với mức ý nghĩa 5%.
Đơn vị: 1000 đồng
| 2002 | 2004 | 2006 | 2008 | 2010 | 2012 | 2014 | 2016 | 2018 | 2019 | 2020 | |
| A | 358 | 498 | 666 | 1065 | 1580 | 2351 | 3265 | 3883 | 4775 | 5190.7 | 5084.1 |
| B | 371 | 471 | 628 | 940 | 1247 | 1797 | 2327 | 2778 | 3585 | 3886.4 | 3874.1 |
Hình 15.6. Thu nhập bình quân đầu khẩu/ tháng ở hai địa phương A và B
VẬN DỤNG
Thời gian ngủ trung bình/ngày của trẻ 3 tuổi được khuyến cáo là 13 giờ. Bảng sau cho số liệu quan sát số giờ ngủ/ngày của 20 trẻ 3 tuổi ở địa phương A:
| 14 | 12 | 13 | 15 | 11 | 10 | 12 | 11 | 13 | 10 |
| 9 | 12 | 14 | 11 | 13 | 10 | 11 | 14 | 12 | 11 |
Em hãy cho biết với mức ý nghĩa 5% có thể cho rằng trẻ 3 tuổi ở địa phương A có số giờ ngủ/ngày khác với khuyến cáo trên hay không.
(Trang 91)
BẢNG GIẢI THÍCH THUẬT NGỮ
| Thuật ngữ | Giải thích | Trang | |
| Đ | Đồng bộ dữ liệu | Quá trình thiết lập tính nhất quán giữa các kho lưu trữ dữ liệu nguồn và đích liên tục theo thời gian. | 50 |
| Đường găng | Đường xuyên suốt đi từ thời điểm bắt đầu đến thời điểm kết thúc dự án, xác định thời gian ngắn nhất cần thiết để hoàn thành toàn bộ dự án. Đường găng bao gồm chuỗi các nhiệm vụ mà sự trì hoãn thực hiện bất kì nhiệm vụ nào trong chuỗi đó sẽ dẫn đến sự kéo dài thời gian thực hiện của cả dự án. Nếu biểu đồ Gantt cung cấp một cái nhìn tổng quan về lịch trình và tiến độ của tất cả các công việc trong dự án, thì đường găng tập trung vào việc xác định các công việc chính yếu ảnh hưởng trực tiếp đến thời gian hoàn thành dự án. | 21 | |
| H | Hệ số tương quan tuyến tính | Hệ số xác định xu hướng và mức độ tương quan tuyến tính của hai biến số X, Y. Ví dụ: Khi R(X, Y) > 0 thì X, Y, cùng tăng hoặc cùng giảm. Ngược lại, R(X, Y) < 0 thì X tăng Y giảm hoặc X giảm Y tăng. | R(X, Y) | > | R(X, Z) | thì X, Y tương quan mạnh hơn X, Z. | 82 |
| K | Khôi phục dữ liệu | Hoạt động ngược lại với sao lưu, sử dụng dữ liệu sao lưu để trả lại trạng thái dữ liệu tại thời điểm sao lưu. Hoạt động này thường được dùng để khôi phục trạng thái của hệ thống khi dữ liệu bị hỏng hay mất vì một lí do nào đó. | 44 |
| N | Nén dữ liệu | Mã hoá dữ liệu theo cách làm giảm kích thước để tăng hiệu quả lưu trữ hay truyền dữ liệu. | 36 |
| Nguồn lực dự án | Nhân sự, tài chính, thời gian, cơ sở vật chất, kĩ thuật,... cần cho việc thực hiện dự án. Trong phạm vi Chuyên đề, chỉ quan tâm ba nguồn lực quan trọng nhất: nhân sự, tài chính và thời gian thực hiện dự án. | 5 | |
| Nhiệm vụ găng (critical task) | Nhiệm vụ không được phép trì hoãn. Điểm chính của nhiệm vụ găng là nó không có “thời gian dự phòng”. Điều này có nghĩa là bất kì sự chậm trễ nào trong việc hoàn thành một nhiệm vụ găng sẽ ảnh hưởng trực tiếp đến tiến độ thực hiện toàn bộ dự án. | 21 | |
| Q | Quản lí dự án | Việc áp dụng các kiến thức, kĩ năng, công cụ và kĩ thuật để phối hợp các hoạt động thực hiện dự án nhằm đáp ứng các yêu cầu của dự án trong phạm vi giới hạn về nguồn lực. | 5 |
| S | Sao lưu dữ liệu | Hoạt động sao chép dữ liệu tại một thời điểm nào đó đưa vào lưu trữ để sử dụng khi cần. | 37 |
| Sai lầm loại 1 | Trường hợp kết quả kiểm định cho rằng có một hiệu ứng hoặc mối quan hệ đáng kể, trong khi trên thực tế không có hiệu ứng hoặc mối quan hệ nào tồn tại. Đây là sai lầm xảy ra khi bác bỏ giả thuyết gốc (giả thuyết H0) mặc dù nó đúng. Mức độ chấp nhận được của sai lầm loại 1 thường được xác định trước khi thực hiện kiểm định và được biểu thị bằng giá trị a, phổ biến nhất a = 0.05, có nghĩa là có một sự chấp nhận 5% nguy cơ sai lầm loại 1. | 86 | |
| T | Tần suất sao lưu | Số lần sao lưu trong một khoảng thời gian xác định. | 45 |

































































Bình Luận
Để Lại Bình Luận Của Bạn