Bài 1. Khái niệm về khối đa diện | Bài giải HÌNH HỌC 12 | CHƯƠNG I. KHỐI ĐA DIỆN - Lớp 12 - Sách Bài Giải

Câu hỏi 1 trang 4 SGK

Nhắc lại định nghĩa hình lăng trụ và hình chóp.

Lời giải:

- Hình lăng trụ là hình gồm có hai đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song, các mặt bên là hình bình hành, các cạnh bên bằng nhau và song song với nhau.

- Hình chóp là một hình không gian gồm có một đa giác gọi là mặt đáy, các tam giác chung đỉnh gọi là mặt bên, đỉnh chung của các mặt bên đó gọi là đỉnh của hình chóp.

Câu hỏi 2 trang 6 SGK

Kể tên các mặt của hình lăng trụ ABCDE.A’B’C’D’E’ và hình chóp S.ABCDE (h.1.4 ).

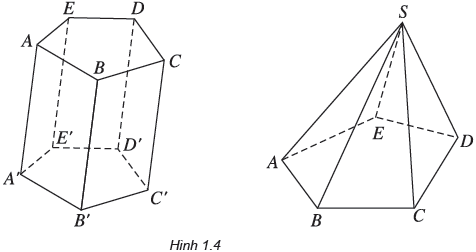
Lời giải:

- Các mặt của hình lăng trụ ABCDE.A’B’C’D’E’là: ABB’A’, BCC’B’, CDD’C’, DEE’D’, EAA’E’, ABCDE, A’B’C’D’E’.

- Các mặt của hình chóp S.ABCDE là: SAB, SBC, SCD, SDE, SAE, ABCDE.

Câu hỏi 3 trang 8 SGK

Giải thích tại sao hình 1.8c không phải là một khối đa diện?

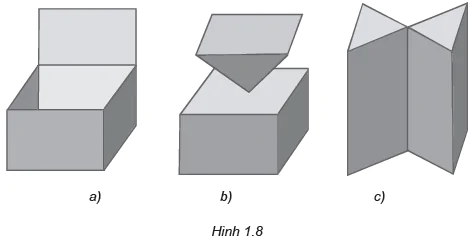
Lời giải:

Hình đa diện có tính chất: Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác

Nhưng hình 1.8c có cạnh AB là cạnh chung có 4 đa giác (không thỏa mãn t/c)

Câu hỏi 4 trang 10 SGK

Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng hai lăng trụ ABD.A’B’D’ và BCD.B’C’D’ bằng nhau.

Lời giải:

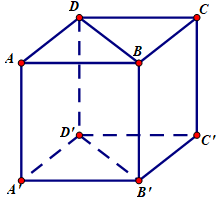
Phép đối xứng qua mặt phẳng (BDD’B’) biến lăng trụ ABD.A’B’D’ thành BCD.B’C’D’

⇒ hai lăng trụ ABD.A’B’D’ và BCD.B’C’D’ bằng nhau.

Bài 1 trang 12 SGK

Chứng minh rằng một đa diện có các mặt là những tam giác thì tổng số các mặt của nó phải là một số chẵn. Cho ví dụ.

Lời giải:

* Gọi a là số cạnh, b là số mặt của khối đa diện.

Nếu khối đa diện có các mặt là tam giác thì mỗi mặt có ba cạnh. Trong ba cạnh đó mỗi cạnh lần lượt là cạnh chung của hai mặt.

Ta có 3b = 2a. Nghĩa là b chẵn.

Mà 2a chia hết cho 2 nên 3b cũng chia hết cho 2

⇒ b chia hết cho 2 hay b là số chẵn.

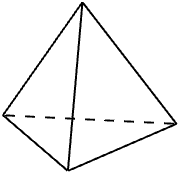
* Ví dụ: hình tứ diện đều có 4 mặt.

Bài 2 trang 12 SGK

Chứng minh rằng một đa diện mà mỗi đỉnh của nó là đỉnh chung của một số lẻ mặt thì tổng số các đỉnh của nó phải là một số chẵn. Cho ví dụ.

Lời giải:

Cho khối đa diện (G) có các đỉnh là B₁, B₂,…, B_n và gọi m₁, m₂,…, m_n lần lượt là số các mặt của (G) nhận chúng làm đỉnh chung, ở đó m₁, m₂,…, m_n là những số lẻ.

Như vậy mỗi đỉnh B_k có m_k cạnh đi qua.

Ta có: đỉnh B₁ có m₁ cạnh đi qua, đỉnh B₂ có m₂ cạnh đi qua, …, đỉnh B_n có m_n cạnh đi qua. 

Do đó tổng số các cạnh (có thể trùng nhau) của đa diện là m₁ + m₂ + … + m_n.

Tuy nhiên, do mỗi cạnh là cạnh chung của đúng hai mặt nên số cạnh ở trên được đếm hai lần.

Vậy tổng số các cạnh thực tế của (G) là:

C = 1/2 (m₁ + m₂ + … + m_n)

Vì C là số nguyên dương nên:

m₁ + m₂ + … + m_n là số chẵn.

Đồng thời m₁, m₂ , ..., m_n là n số tự nhiên lẻ nên tổng của chúng là số chẵn khi n chẵn.

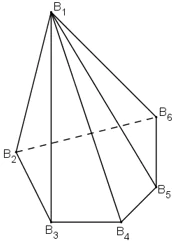
Ví dụ: Hình chóp ngũ giác B₁B₂B₃B₄B₅B₆ có: B₁ là đỉnh chung của 5 mặt bên. Mỗi đỉnh B₁, B₂, B₃, B₄, B₅, B₆ là đỉnh chung của ba mặt (hình dưới).

Bài 3 trang 12 SGK

Chia một khối lập phương thành năm khối tứ diện.

Lời giải:

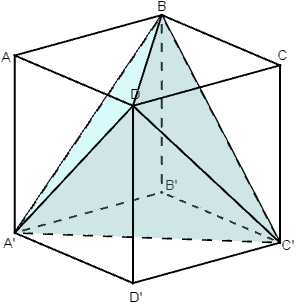
Trong hình bên, ta có thể chia thành năm khối tứ diện là A’ABD; C’CBD; DA’D’C’; BB’A’C’ (4 góc của hình lập phương) và DBA’C’ (tứ diện tô màu).

Bài 4 trang 12 SGK

Chia một khối lập phương thành sáu khối tứ diện bằng nhau.

Lời giải:

Ta chia hình lập phương thành sáu khối tứ diện bằng nhau như sau:

+ Chia khối lập phương ABCD.A’B’C’D’ thành hai khối lăng trụ tam giác bằng nhau: ABD.A’B’D’ và BCD.B’C’D’.

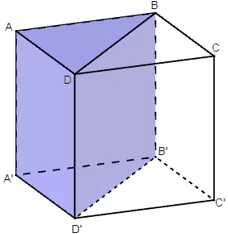
+ Tiếp đó, lần lượt chia khối lăng trụ ABD.A’B’D’ và BCD.B’C’D’ thành ba khối tứ diện: DABB’, DAA’B’, DD’A’B’ và DCBB’, DCC’B’, DD’C’B’.

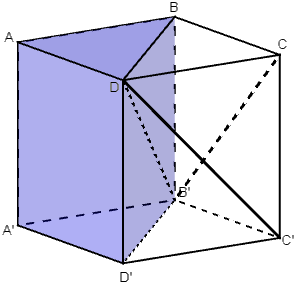
+ Ta chứng minh được các khối tứ diện này bằng nhau như sau:

- Hai khối tứ diện DABB’ và DAA’B’ bằng nhau vì chúng đối xứng nhau qua mặt phẳng (DAB’) (1)

- Hai khối tứ diện DAA’B’ và DD’A’B’ bằng nhau vì chúng đối xứng nhau qua mặt phẳng (B’A’D) (2)

Từ (1) và (2) suy ra ba khối tứ diện DABB’, DAA’B’ và DD’A’B’ bằng nhau.

- Tương tự, ba khối tứ diện DCBB’, DCC’B’, DD’C’B’ cũng bằng nhau.

Vậy khối lập phương ABCD.A’B’C’D’ được chia thành sáu khối tứ diện bằng nhau.