Bài 32: QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN | Toán 7 - Tập 2 | CHƯƠNG IX: QUAN HỆ GIỮA CÁC YÊU TÔ TRONG MỘT TAM GIÁC - Lớp 7 - Kết Nối Tri Thức Với Cuộc Sống

Trang 63

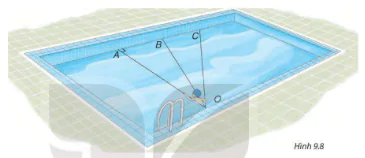
Hình 9.8

Bạn Nam tập bơi ở một bể bơi hình chữ nhật, trong đó có ba đường bơi OA, OB và OC. Biết rằng OA vuông góc với cạnh của bể bơi (H.9.8).

Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì bạn Nam nên chọn đường bơi nào?

Khái niệm đường vuông gốc và đường xiên

Từ một điểm A không nằm trên đường thẳng d, kẻ đường thẳng vuông góc với d tại H (H.9.9).

Đoạn thẳng AH gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng d. Ta gọi H là chân đường vuông góc hạ từ A xuống d.

Lấy một điểm M trên d (M khác H), kẻ đoạn thẳng AM. Đoạn thẳng AM gọi là một đường xiên kẻ từ A đến đường thẳng d.

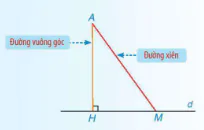
Hình 9.9

Trang 64

So sánh đường vuông góc và đường xiên

HĐ. Cho điểm A không nằm trên đường thẳng d.

a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.

b) Em hãy giải thích vì sao AH < AM.

Dùng quan hệ giữa góc và cạnh đối diện trong tam giác AHM để giải thích nhé!

Từ HĐ trên, ta suy ra định lí sau:

Định lí

Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.

Chú ý. Vì độ dài đoạn thẳng AH là ngắn nhất trong các đoạn thẳng kẻ từ A đến d nên độ dài đoạn thẳng AH được gọi là khoảng cách từ điểm A đến đường thẳng d (H.9.9).

Khi điểm A nằm trên đường thẳng d, người ta coi khoảng cách từ A đến ở bằng 0.

Luyện tập

Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.

a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.

b) So sánh hai đoạn thẳng AB và AM

c) Tìm khoảng cách từ điểm C đến đường thẳng AB.

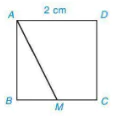
Hình 9.10

Vận dụng

Em hãy trả lời câu hỏi trong tình huống mở đầu.

Thử thách nhỏ

a) Quan sát Hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì độ dài AM càng lớn, tức là nếu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.

b) Xét hình vuông ABCD và một điểm M tuỳ ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?

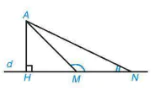
Hình 9.11

Trang 65

BÀI TẬP

9.6. Chiều cao của tam giác ứng với một cạnh của nó có phải là khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó không?

9.7. Cho hình vuông ABCD. Hỏi trong bốn đỉnh của hình vuông

a) Đỉnh nào cách đều hai điểm A và C?

b) Đỉnh nào cách đểu hai đường thẳng AB và AD?

9.8. Cho tam giác cân ABC, AB = AC. Lấy điểm M tuỳ ý nằm giữa B và C (H.9.12).

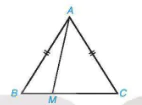
Hình 9.12

a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.

b) Chứng minh rằng với mọi điểm M thì AM < AB.

9.9. Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC (M, N không phải là đỉnh của tam giác) (H.9.13). Chứng minh rằng MN < BC. (Gợi ý. So sánh MN với NB, NB với BC).

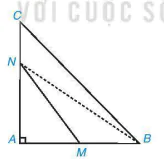
Hình 9.13