LUYỆN TẬP CHUNG (TRANG 82) | Toán 7 - Tập 2 | CHƯƠNG IX: QUAN HỆ GIỮA CÁC YÊU TÔ TRONG MỘT TAM GIÁC - Lớp 7 - Kết Nối Tri Thức Với Cuộc Sống

Trang 82

Ví dụ 1

Chứng minh rằng tam giác ABC có đường trung tuyến AM cũng là đường phân giác thì ABC là tam giác cân tại A.

Giải (H.9.49)

GT	Δ ABC, BM = CM = .
KL	AB = AC.

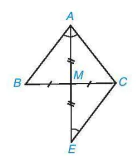
Hình 9.49

Chứng minh

Trên đường thẳng AM, lấy điểm E sao cho M nằm giữa A, E và AM = EM.

Ta có △BAM = △CEM (c.g.c), suy ra AB = EC và = .

Mặt khác

Ví dụ 2

Cho tam giác ABC có 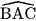= 135°, ba đường cao Al, BJ, CK và trực tâm H (H.9.50). Chứng minh rằng:

a) Tam giác AKC vuông cân, từ đó suy ra AK = CK;

b) Hai tam giác HAK và BCK bằng nhau, từ đó suy ra AH = BC.

Giải

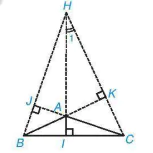
Hình 9.50

Chứng minh

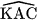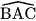a) Ta có và  là hai góc kể bù, = 135°, suy ra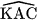

Tam giác KAC vuông tại K có:

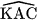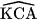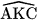+ +  = 180° (tổng ba góc trong tam giác),

hay 45° + 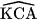+ 90° = 180°, suy ra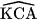

Do đó, tam giác KAC vuông cân tại K, suy ra AK = CK.

Trang 83

b) Tam giác AHK vuông tại K nên +  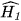= 90°.

Tam giác HIC vuông tại I nên  + 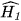= 90°. Do đó

Hai tam giác HAK và BCK có:

AK = CK (chứng minh câu a);

= ;

=

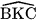
Do đó, △HAK = △BCK (g.c.g), suy ra AH = BC.

BÀI TẬP

9.31. Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.

9.32. Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với đường thẳng AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳng CM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chứng minh đường thẳng BM vuông góc với đường thẳng CN.

9.33. Có một mảnh tôn hình tròn cần đục một lỗ ở tâm. Làm thế nào để xác định được tâm của mảnh tôn đó?

9.34. Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của tia AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.

9.35. Kí hiệu S_ABC là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC.

a) Chứng minh S_G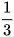BC = S_ABC.

Gợi ý. Sử dụng GM = 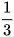AM để chứng minh S_GBM = 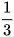S_ACM, S_G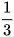CM=S_ACM.

b) Chứng minh S_GCA = S_GAB =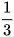

Nhận xét. Từ bài tập trên ta có: S_GBC =  S_GCA = S_GAB = 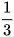S_ABC, điều này giúp ta cảm nhận tại sao có thể đặt thăng bằng miếng bìa hình tam giác trên giá nhọn đặt tại trọng tâm của tam giác đó.