Trang 20
| THUẬT NGỮ • Tiệm cận ngang • Tiệm cận đứng • Tiệm cận xiên | KIẾN THỨC, KĨ NĂNG Nhận biết hình ảnh hình học của đường tiệm cận ngang, đường tiệm cận đứng, đường tiệm cận xiên của đồ thị hàm số. |
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau 1 ngày phân rã được cho bởi hàm số
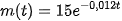
Khối lượng m(t) thay đổi ra sao khi t → +∞? Điều này thể hiện trên Hình 1.18 như thế nào?
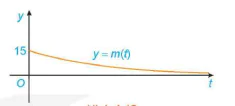
Hình 1.18
1. ĐƯỜNG TIỆM CẬN NGANG
HĐ1. Nhận biết đường tiệm cận ngang
Cho hàm số 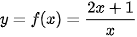 có đồ thị (C). Với x > 0, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng y = 2 (H.1.19).
có đồ thị (C). Với x > 0, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng y = 2 (H.1.19).
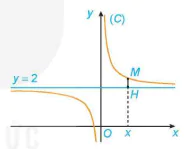
Hình 1.19
a) Tính khoảng cách MH.
b) Có nhận xét gì về khoảng cách MH khi x → +∞?
| Đường thẳng y =
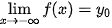 . . |
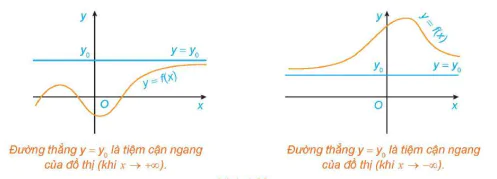
Đường thẳng y = 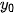 là tiệm cận ngang của đồ thị (khi x → +∞).
là tiệm cận ngang của đồ thị (khi x → +∞).
Đường thẳng y = 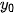 là tiệm cận ngang của đô thị (khi x → -∞)
là tiệm cận ngang của đô thị (khi x → -∞)
Hình 1.20
Ví dụ 1. Tìm tiệm cận ngang của đồ thị hàm số 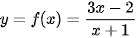
Giải
3
Ta có: 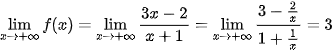 . Tương tự,
. Tương tự, 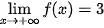 .
.
Vậy đồ thị hàm số f(x) có tiệm cận ngang là đường thẳng y = 3.
Ví dụ 2. Tìm các tiệm cận ngang của đồ thị hàm số 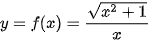 .
.
Giải
Ta có:
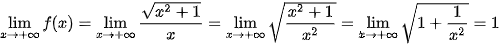 ;
;
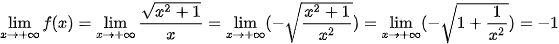
Vậy đồ thị hàm số f(x) có hai tiệm cận ngang là y = 1 và y = -1. Nhận xét. Đồ thị hàm số f(x) như Hình 1.21.
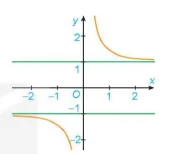
Hình 1.21
Luyện tập 1. Tìm tiệm cận ngang của đồ thị hàm số 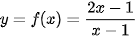 .
.
Vận dụng 1. Giải bài toán trong tình huống mở đầu.
2. ĐƯỜNG TIỆM CẬN ĐỨNG
HĐ2. Nhận biết đường tiệm cận đứng
Cho hàm số 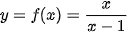 có đồ thị (C). Với x > 1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng x = 1 (H.1.22).
có đồ thị (C). Với x > 1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng x = 1 (H.1.22).
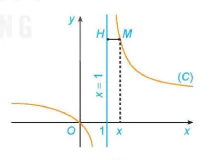
Hình 1.22
a) Tính khoảng cách MH.
b) Khi M thay đổi trên (C) sao cho khoảng cách MH dần đến 0, có nhận xét gì về tung độ của điểm M?
Đường thẳng x = 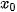 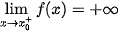 ; ; 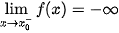 ; ; 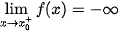 ; ; 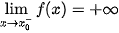 . . |
Trang 22
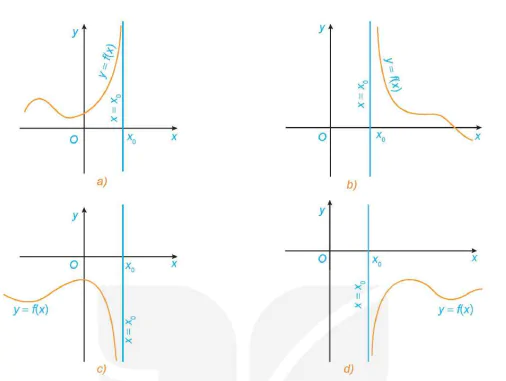
a) và c). Đường thẳng x = 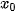 là tiệm cận đứng của đồ thị (khi x →
là tiệm cận đứng của đồ thị (khi x → 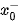 )
)
b) và d). Đường thẳng x = 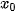 là tiệm cận đứng của đồ thị (khi x →
là tiệm cận đứng của đồ thị (khi x → 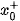 ).
).
Hình 1.23
Ví dụ 3. Tìm tiệm cận đứng của đồ thị hàm số 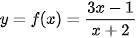
Giải
Ta có: 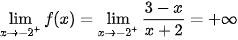 . Tương tự,
. Tương tự, 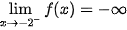 . Vậy đồ thị hàm số f(x) có tiệm cận đứng là đường thẳng x = −2.
. Vậy đồ thị hàm số f(x) có tiệm cận đứng là đường thẳng x = −2.
Ví dụ 4. Tìm tiệm cận đứng của đồ thị hàm số 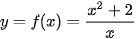 .
.
Giải
Ta có: 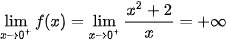 . Tương tự,
. Tương tự, 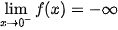
Luyện tập 2. Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 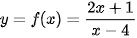 .
.
Vận dụng 2. Để loại bỏ p% một loài tảo độc khỏi một hồ nước, người ta ước tính chi phí bỏ ra là
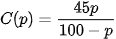 (triệu đồng), với 0 ≤ p ≤ 100.
(triệu đồng), với 0 ≤ p ≤ 100.
Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa thực tiễn của đường tiệm cận này.
Trang 23
3. ĐƯỜNG TIỆM CẬN XIÊN
HĐ3. Nhận biết đường tiệm cận xiên
Cho hàm số 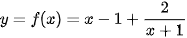 có đồ thị (C) và đường thẳng y = x − 1 như Hình 1.24.
có đồ thị (C) và đường thẳng y = x − 1 như Hình 1.24.
a) Với x > −1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng y = x − 1. Có nhận xét gì về khoảng cách MH khi x → +∞?
b) Chứng tỏ rằng 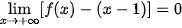 . Tính chất này thể hiện trên Hình 1.24 như thế nào?
. Tính chất này thể hiện trên Hình 1.24 như thế nào?
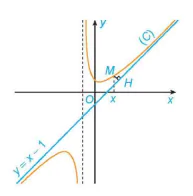
Hình 1.24
Đường thẳng y = ax + b (a ≠ 0) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu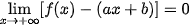 hoặc hoặc 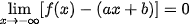 . . |
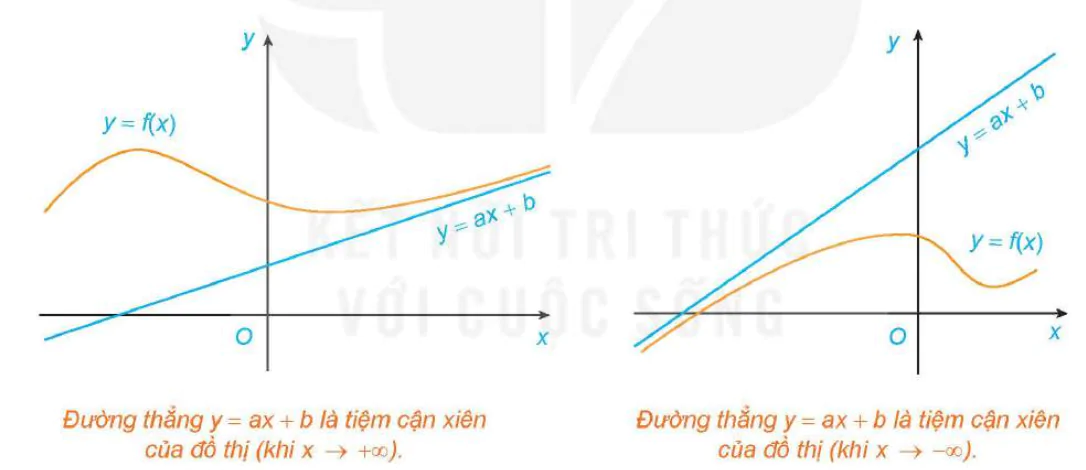
Đường thẳng y = ax + b là tiệm cận xiên của đồ thị (khi x → +∞).
Đường thẳng y = ax + b là tiệm cận xiên của đô thị (khi x → -∞)
Hình 1.25
Ví dụ 5. Cho hàm số 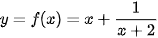 . Tìm tiệm cận xiên của đồ thị hàm số f(x).
. Tìm tiệm cận xiên của đồ thị hàm số f(x).
Giải
Ta có: 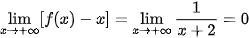
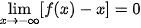 .
. Vậy đồ thị hàm số f(x) có tiệm cận xiên là đường thẳng y = x.

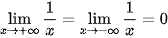 .
.
Trang 24
Chú ý. Ta biết rằng nếu đường thẳng y = ax + b (a ≠ 0) là tiệm cận xiên của đồ thị hàm số y = f(x) thì 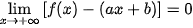 hoặc
hoặc 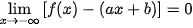
Do đó 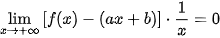 hoặc
hoặc 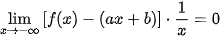 .
.
Từ đây suy ra 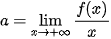 hoặc
hoặc 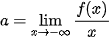 .
.
Khi đó, ta có 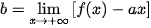
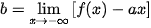 .
. Ngược lại, với a và b xác định như trên, đường thẳng y = ax + b (a ≠ 0) là một tiệm cận xiên của đồ thị hàm số y = f(x). Đặc biệt, nếu a = 0 thì đồ thị hàm số có tiệm cận ngang.
Ví dụ 6. Tìm tiệm cận xiên của đồ thị hàm số 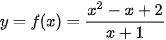 .
.
Giải
Ta có:
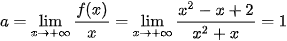 ;
;
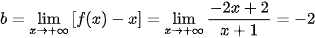 .
.
(Tương tự, 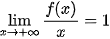
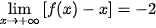 .)
.) Vậy đồ thị hàm số f(x) có tiệm cận xiên là đường thẳng y = x - 2.
Nhận xét. Trong thực hành, để tìm tiệm cận xiên của hàm phân thức trong Ví dụ 6, ta viết:
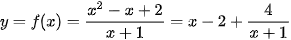 .
.
Ta có: 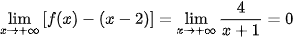 ;
;
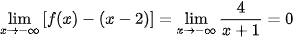 .
.
Do đó, đồ thị hàm số f(x) có tiệm cận xiên là đường thẳng y = x – 2.
Luyện tập 3. Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số 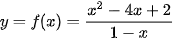
Trang 25
BÀI TẬP
1.16. Hình 1.26 là đồ thị của hàm số 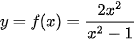 .
.
Sử dụng đồ thị này, hãy
a) Viết kết quả của các giới hạn sau: 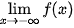 ;
; 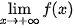 ;
; 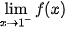 ;
; 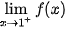
b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.
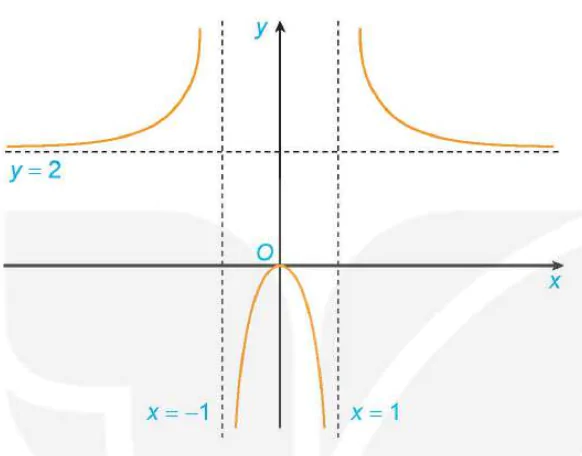
Hình 1.26
1.17. Đường thẳng x = 1 có phải là tiệm cận đứng của đồ thị hàm số 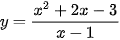 không?
không?
1.18. Tìm các tiệm cận của đồ thị các hàm số sau:
a) 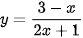 ;
;
b) 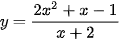 .
.
1.19. Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là
C(x) = 2x + 50 (triệu đồng).
Khi đó f(x) = C(x) là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và 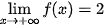
1.20. Một mảnh vườn hình chữ nhật có diện tích bằng 144 m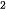 . Biết độ dài một cạnh của mảnh vườn là x (m).
. Biết độ dài một cạnh của mảnh vườn là x (m).
a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn.
b) Tìm các tiệm cận của đồ thị hàm số P(x).




































































Bình Luận
Để Lại Bình Luận Của Bạn