Trang 80
| THUẬT NGỮ • Phương sai • Độ lệch chuẩn | KIẾN THỨC, KĨ NĂNG • Tính phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm. • Hiểu ý nghĩa, vai trò của phương sai, độ lệch chuẩn trong việc đo mức độ phân tán. |
Để xác định độ ổn định của một máy đo độ ẩm không khí, người ta dùng máy này để đo 20 lần. Nếu độ lệch chuẩn của mẫu số liệu đo lớn hơn 0,15 thì người ta sẽ đưa máy đo đi sửa chữa. Trong một lần lấy mẫu, kĩ thuật viên có được mẫu số liệu ghép nhóm sau:
| Độ ẩm (%) | [52; 52,1) | [52,1; 52,2) | [52,2; 52,3) | [52,3; 52,4) | [52,4; 52,5) |
| Tần số | 1 | 5 | 8 | 4 | 2 |
Liệu có cần đưa máy đo này đi sửa chữa hay không?
1. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN
HĐ1. Trở lại bài toán trong tình huống mở đầu. Gọi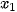 
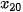là các kết quả đo (mẫu số liệu gốc). a) Có thể tính được chính xác phương sai và độ lệch chuẩn của mẫu số liệu gốc hay không?
b) Thảo luận và đề xuất ước lượng cho phương sai và độ lệch chuẩn của mẫu số liệu gốc.
Xét mẫu số liệu ghép nhóm cho bởi Bảng 3.1.
• Phương sai của mẫu số liệu ghép nhóm, kí hiệu là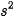 
, là một số được tính theo công thức sau:
;
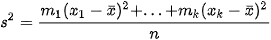trong đó,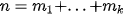 
; 
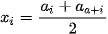
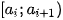và 
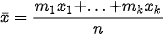. X là số trung bình của mẫu số liệu ghép nhóm.• Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là
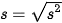. Nhận xét. Ta có thể tính phương sai theo công thức: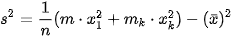 
.
Độ lệch chuẩn có cùng đơn vị với đơn vị của mẫu số liệu.
Trang 81
Ý nghĩa. Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm là các xấp xỉ cho phương sai, độ lệch chuẩn của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Phương sai, độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Chú ý. Người ta còn sử dụng các đại lượng sau để đo mức độ phân tán của mẫu số liệu ghép nhóm:
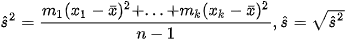
Ví dụ 1. Người ta theo dõi sự thay đổi cân nặng, được tính bằng hiệu cân nặng trước và sau ba tháng áp dụng chế độ ăn kiêng của một số người cho kết quả như sau:
| Thay đổi cân nặng (kg) | [-1; 0) | [0; 1) | [1; 2) | [2; 3) | [3; 4) |
| Số người nam | 2 | 3 | 5 | 3 | 2 |
| Số người nữ | 2 | 7 | 12 | 7 | 2 |
Tính số trung bình, phương sai, độ lệch chuẩn và nhận xét về sự thay đổi cân nặng của người nam, người nữ sau ba tháng áp dụng chế độ ăn kiêng.
Giải
Chọn giá trị đại diện cho các nhóm số liệu, ta có:
| Giá trị đại diện | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 |
| Số người nam | 2 | 3 | 5 | 3 | 2 |
| Số người nữ | 2 | 7 | 12 | 7 | 2 |
Tổng số người nam là: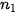 
= 2 + 3 + 5 + 3 + 2 = 15.
Tổng số người nữ là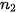 
= 2 + 7 + 12 + 7 + 2 = 30.
Thay đổi cân nặng trung bình của người nam là:
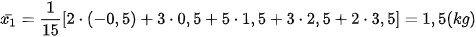. 3-25 + 2-3,5-1,5 (k
Thay đổi cân nặng trung bình của người nữ là: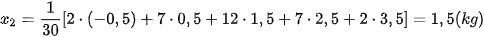
.
Phương sai và độ lệch chuẩn của mẫu số liệu về thay đổi cân nặng của người nam là
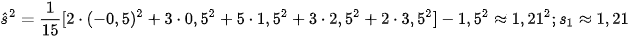
Phương sai và độ lệch chuẩn của mẫu số liệu về thay đổi cân nặng của người nữ là
.
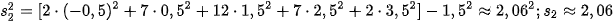Như vậy, sau ba tháng áp dụng chế độ ăn kiêng này, về trung bình sự thay đổi cân nặng của nam và nữ là như nhau. Tuy nhiên, sự biến động về thay đổi cân nặng của nữ nhiều hơn so với của nam.
Trang 82
Luyện tập 1. Một vận động viên luyện tập chạy cự li 100 m đã ghi lại kết quả luyện tập như sau:
| Thời gian (giây) | [10,2; 10,4) | [10,4; 10,6) | [10,6; 10,8) | [10,8; 11) |
| Số vận động viên | 3 | 7 | 8 | 2 |
Tìm phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm này. Phương sai và độ lệch chuẩn cho biết điều gì?
Vận dụng. Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm cho bài toán trong tình huống mỏ đầu và cho biết có cần đưa máy đi sửa chữa hay không.
2. SỬ DỤNG PHƯƠNG SAI, ĐỘ LỆCH CHUẨN ĐO ĐỘ RỦI RO
Trong tài chính, người ta có nhiều cách để đo độ rủi ro của một phương án đầu tư. Một trong các cách đó là sử dụng độ lệch chuẩn của lợi nhuận thu được theo phương án đầu tư. Độ lệch chuẩn càng lớn thì phương án đầu tư càng rủi ro.
Ví dụ 2. Anh An đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh An thống kê số tiền thu được mỗi tháng trong vòng 60 tháng theo mỗi lĩnh vực cho kết quả như sau:
| Số tiền (triệu đồng) | [5; 10) | [10; 15) | [15; 20) | [20; 25) | [25; 30) |
| Số tháng đầu tư vào lĩnh vực A | 5 | 10 | 30 | 10 | 5 |
| Số tháng đầu tư vào lĩnh vực B | 20 | 5 | 10 | 5 | 20 |
So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực A, B. Đầu tư vào lĩnh vực nào "rủi ro" hơn?
Giải
Chọn giá trị đại diện cho các nhóm số liệu ta có:
| Giá đại diện | 7,5 | 12,5 | 17,5 | 22,5 | 27,5 |
| Số tháng đầu tư vào lĩnh vực A | 5 | 10 | 30 | 10 | 5 |
| Số tháng đầu tư vào lĩnh vực B | 20 | 5 | 10 | 5 | 20 |
Số tiền trung bình thu được khi đầu tư vào các lĩnh vực A, B tương ứng là
;
.
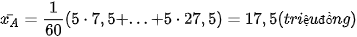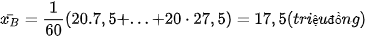Như vậy, về trung bình đầu tư vào các lĩnh vực A, B số tiền thu được hàng tháng như nhau. Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực A, B tương ứng là
;
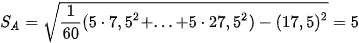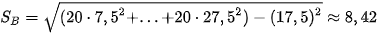
Trang 83
Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực B cao hơn khi đầu tư vào lĩnh vực A. Người ta nói rằng, đầu tư vào lĩnh vực B là "rủi ro" hơn.
Ví dụ sau cho thấy không phải lúc nào ta cũng có thể dùng độ lệch chuẩn của lợi nhuận thu được để so sánh độ rủi ro của các phương án đầu tư.
Ví dụ 3. Thống kê lợi nhuận hàng tháng (đơn vị: triệu đồng) trong 20 tháng của hai nhà đầu tư được cho như sau:
| Lợi nhuận | [10; 20) | [20; 30) | [30; 40) | [40; 50) | [50; 60) |
| Số tháng | 2 | 4 | 8 | 4 | 2 |
Bảng 3.2. Lợi nhuận theo tháng của nhà đầu tư nhỏ
| Lợi nhuận | [510; 520) | [520; 530) | [530; 540) | [540; 550) | [550; 560) |
| Số tháng | 4 | 3 | 6 | 3 | 4 |
Bảng 3.3. Lợi nhuận theo tháng của nhà đầu tư lớn
Tính độ lệch chuẩn của hai mẫu số liệu ghép nhóm trên. Có nên dựa vào độ lệch chuẩn để so sánh độ rủi ro của hai nhà đầu tư này không?
Giải
Chọn điểm đại diện cho các nhóm số liệu ta tính được các số đặc trưng như sau:
Lợi nhuận trung bình một tháng của các nhà đầu tư tương ứng là:
; 
.
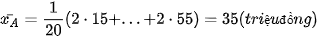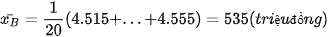Độ lệch chuẩn của lợi nhuận hàng tháng của hai nhà đầu tư tương ứng là:
; 
.
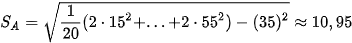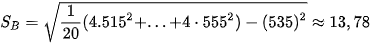Độ lệch chuẩn cho lợi nhuận hàng tháng của nhà đầu tư lớn cao hơn của nhà đầu tư nhỏ. Lợi nhuận trung bình của hai nhà đầu tư khác nhau rất nhiều, do đó ta không nên dùng độ lệch chuẩn để so sánh mức độ rủi ro của hai nhà đầu tư này.
Nhận xét. Ta không nên dùng phương sai hay độ lệch chuẩn để so sánh độ rủi ro của hai phương án đầu tư khi lợi nhuận trung bình của hai phương án đầu tư này khác nhau rất nhiều.
Em có biết?
Để so sánh độ phân tán của hai mẫu số liệu khi đơn vị đo trên hai mẫu số liệu khác nhau hoặc giá trị trung bình của hai mẫu số liệu này khác nhau rất nhiều người ta dùng hệ số biến thiên CV (Coefficient of Variation). Hệ số biến thiên được tính theo công thức
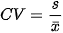
trong đó s là độ lệch chuẩn và x là số trung bình của mẫu số liệu.
Trang 84
BÀI TẬP
3.4. Kiểm tra khối lượng của 30 bao xi măng (đơn vị: kg) được chọn ngẫu nhiên trước khi xuất xưởng cho kết quả như sau:
49,5 51,1 50,8 50,2 48,7 49,6 51,3 51,4 50,1 50,5
48,9 49,3 50,7 48,8 49,8 48,8 51,2 50,4 50,0 51,2
51,4 48,7 51,2 50,6 50,9 49,2 50,7 51,1 48,6 49,6.
a) Thay dấu "?" bằng số thích hợp để hoàn thiện mẫu số liệu ghép nhóm sau.
| Nhóm số liệu | [48,5; 49) | [49; 49,5) | [49,5; 50) | [50; 50,5) | [50,5; 51) | [51; 51,5) |
| Số bao xi măng | ? | ? | ? | ? | ? | ? |
b) Tính phương sai và độ lệch chuẩn của mẫu số liệu gốc và mẫu số liệu ghép nhóm. Giá trị nào là giá trị chính xác? Giá trị nào là giá trị xấp xỉ?
3.5. Tuổi thọ của một số linh kiện điện tử (đơn vị: năm) được sản xuất bởi hai phân xưởng được cho như sau:
| Tuổi thọ (năm) | [1,5; 2) | [2; 2,5) | [2,5; 3) | [3; 3,5) | [3,5; 4) |
| Số linh kiện của phân xưởng 1 | 4 | 9 | 13 | 8 | 6 |
| Số linh kiện của phân xưởng 2 | 8 | 20 | 7 | 3 | 2 |
Tính phương sai và độ lệch chuẩn của mỗi mẫu số liệu ghép nhóm và nhận xét về độ phân tán của tuổi thọ các linh kiện điện tử được sản xuất bởi mỗi phân xưởng.
3.6. Một nhóm 20 học sinh dùng một thiết bị đo đường kính của một nhân tế bảo cho kết quả như sau:
| Kết quả đo (μm) | [4,5; 5) | [5; 5,5) | [5,5; 6) | [6; 6,5) |
| Số học sinh | 3 | 8 | 7 | 2 |
a) Tính số trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
b) Số trung bình và độ lệch chuẩn cho biết thông tin gì?
3.7. Thời gian chạy tập luyện cự li 100 m của hai vận động viên được cho trong bảng sau:
| Thời gian (giây) | [10; 10,3) | [10,3; 10,6) | [10,6; 10,9) | [10,9; 11,2) |
| Số lần chạy của A | 2 | 10 | 5 | 3 |
| Số lần chạy của B | 3 | 7 | 9 | 6 |
Dựa trên độ lệch chuẩn của các mẫu số liệu ghép nhóm, hãy cho biết vận động viên nào có thành tích luyện tập ổn định hơn.
3.8. Có nên dùng phương sai (hoặc độ lệch chuẩn) để so sánh độ phân tán của hai mẫu số liệu ghép nhóm trong mỗi trường hợp sau không? Tại sao?
a) Các mẫu số liệu ghép nhóm về điểm thi tốt nghiệp môn Toán của học sinh hai trường trung học phổ thông có chất lượng tương đương.
b) Các mẫu số liệu ghép nhóm về doanh thu của 100 cửa hàng bán lẻ và doanh thu của 100 siêu thị.
Các Bài Học Khác
Kết nối tri thức - NXB Giáo Dục Việt Nam Toán 12 tập 1 Chương III: Các Số Đặc Trưng Đo Mức Độ Phân Tán Của Mẫu Số Liệu Ghép Nhóm Bài Tập Cuối Chương III
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn