Nội Dung Chính
(Trang 67)
Chương IX ĐƯỜNG TRÒN NGOẠI TIẾP VÀ ĐƯỜNG TRÒN NỘI TIẾP
Trong chương này chúng ta sẽ tìm hiểu về những đường tròn đi qua các đỉnh của tam giác, tứ giác hay lục giác và những đường tròn lớn nhất có thể vẽ được nằm bên trong hình đó. Những đường tròn đó lần lượt được gọi là các đường tròn ngoại tiếp và các đường tròn nội tiếp.
Bài 27 GÓC NỘI TIẾP
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| - Góc nội tiếp - Cung bị chắn | - Nhận biết góc nội tiếp của một đường tròn. - Nhận biết cung bị chắn bởi góc nội tiếp của một đường tròn. - Giải thích mối liên hệ giữa số đo góc nội tiếp với số đo góc ở tâm chắn cùng một cung. |
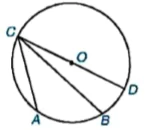
Chúng ta đã biết số đo góc ở tâm BOC của đường tròn (O) trong Hình 9.1 bằng số đo của cung bị chắn 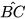
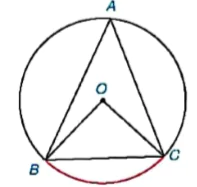
Hình 9.1
(Trang 68)
Góc nội tiếp và cung bị chắnHĐ Vẽ đường tròn tâm O có bán kính bằng 2 cm và dây cung AB có độ dài bằng 2 cm. Lấy một điểm C tuỳ ý nằm trên cung lớn AmB (H.9.2). a) Cho biết số đo của góc ở tâm AOB và số đo của cung bị chắn AB. b) Đo góc ACB và so sánh với kết quả của bạn bên cạnh. |
Hình 9.2 |
| △AOB là tam giác đều. |
Các góc ACB và ADB ở Hình 9.2 được gọi là các góc nội tiếp của đường tròn (O) và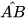 là cung bị chắn.
là cung bị chắn.
Tổng quát, chúng ta có định nghĩa về góc nội tiếp như sau:
Định nghĩa
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong góc được gọi là cung bị chắn.
Ví dụ 1
Trong các góc A, B, C, D ở Hình 9.3, góc nào là góc nội tiếp, góc nào không phải góc nội tiếp? Vì sao?
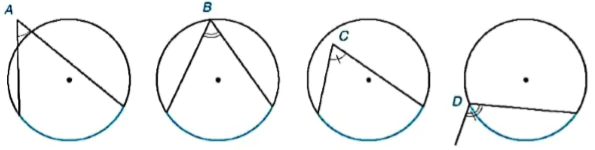
Hình 9.3
Giải
Các góc A và C không phải góc nội tiếp của đường tròn vì đỉnh không nằm trên đường tròn. Góc D có một cạnh không chứa dây cung của đường tròn nên cũng không là góc nội tiếp của đường tròn. Góc B có đỉnh B nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn nên là góc nội tiếp của đường tròn.
(Trang 69)
Định lí sau cho biết mối liên hệ giữa góc nội tiếp với cung bị chắn:
Định lí
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
| GT | A, B, C ∈ (O). |
| KL | 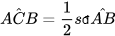 |
Chứng minh. Ta xét ba trường hợp sau (H.9.3).
|
Trường hợp 1 |
Trường hợp 2 |
Trường hợp 3 |
Hình 9.4
Trường hợp 1: Tâm O nằm trên một cạnh của góc ACB. Giả sử O ∈ CB. Do tam giác OAC cân tại O và có tổng các góc bằng 180° nên:
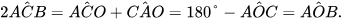
Do 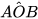
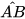 (vì
(vì 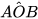 là góc ở tâm chắn cung AB) nên
là góc ở tâm chắn cung AB) nên 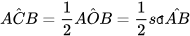
Trường hợp 2: Tâm O nằm bên trong góc ACB. Vẽ đường kính CD. Áp dụng Trường hợp 1 cho các góc nội tiếp ACD và DCB với cạnh CD đi qua O, ta được:
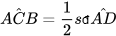 và
và 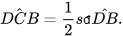
Suy ra 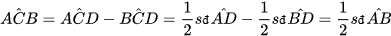 .
.
Nhận xét. Từ định lí trên ta có các khẳng định sau:
• Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
• Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
• Các góc nội tiếp chắn cung nhỏ thì có số đo bằng nửa số đo của góc ở tâm chắn cùng một cung.
• Góc nội tiếp chắn nửa đường tròn là góc vuông.
(Trang 70)
Hãy cho biết số đo góc nội tiếp tìm được trong Hình 9.3 ở Ví dụ 1, biết rằng số đo của các cung màu xanh trong hình đều bằng 120°.
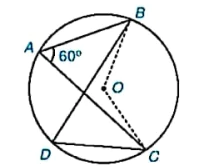
Hình 9.3
Ví dụ 2
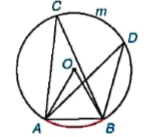
Cho đường tròn (O) và các điểm A, B, C, D trên (O) như Hình 9.5. Biết rằng 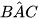 = 60°, hãy tính số đo của các góc BOC và BDC.
= 60°, hãy tính số đo của các góc BOC và BDC.
Giải (H.9.5). Xét đường tròn (O), ta có:
• Do hai góc nội tiếp 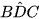 và
và 
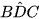 =
=  = 60°;
= 60°;
• Vì góc nội tiếp  và góc ở tâm
và góc ở tâm 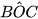 cùng chắn cung nhỏ BC nên
cùng chắn cung nhỏ BC nên
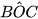
 = 120°.
= 120°. Luyện tập
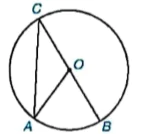
Cho đường tròn tâm O và hai dây cung AB, CD cắt nhau tại điểm X nằm trong đường tròn (H.9.6). Chứng minh rằng △AXC 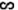 △DXB.
△DXB.
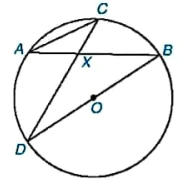
Hình 9.6
Vận dụng
Trở lại tình huống mở đầu, hãy tính số đo của góc BAC nếu biết đường tròn có bán kính 2 cm và dây cung 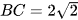 cm.
cm.
 |
BÀI TẬP
9.1. Những khẳng định nào sau đây là đúng?
a) Hai góc nội tiếp bằng nhau thì chắn cùng một cung.
b) Góc nội tiếp nhỏ hơn 90° có số đo bằng nửa số đo của góc ở tâm chắn cùng một cung.
c) Góc nội tiếp chắn cung nhỏ có số đo bằng số đo của góc ở tâm chắn cùng một cung.
d) Hai góc nội tiếp bằng nhau thì chắn hai cung bằng nhau.
(Trang 71)
9.2. Cho các điểm như Hình 9.7. Tính số đo các góc của tam giác ABC, biết rằng 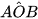 = 120°,
= 120°, 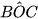 = 80°.
= 80°.
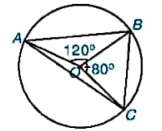
Hình 9.7
9.3. Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X (H.9.8). Tính số đo góc AXB biết rằng 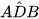 = 30° và
= 30° và 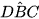
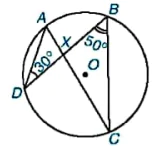
Hình 9.8
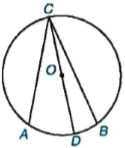
9.4. Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) (H.9.9).
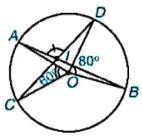
Hình 9.9
a) Biết rằng 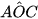 = 60°,
= 60°, 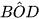 =80°. Tính số đo của góc AID.
=80°. Tính số đo của góc AID.
b) Chứng minh rằng IA.IB = IC .ID.
9.5. Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A) và N (khác B). Gọi P là giao điểm của BM và AN (H.9.10). Chứng minh rằng SP vuông góc või AB.
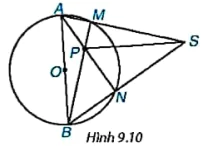
Hình 9.10
9.6. Trên sân bóng, khi trái bóng được đặt tại điểm phạt đền thì có góc sút bằng 36° và trái bóng cách mỗi cọc gôn 11,6 m (H.9.11). Hỏi khi trái bóng đặt ở vị trí cách điểm phạt đến 11,6 m thì góc sút bằng bao nhiêu?
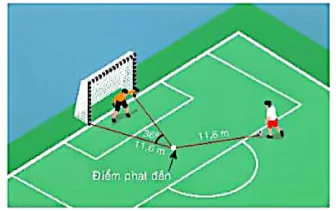
Hình 9.11







































Bình Luận
Để Lại Bình Luận Của Bạn