Nội Dung Chính
(Trang 25)
| Thuật ngữ
| Kiến thức, kĩ năng
|
| Trong Toán học ta thường phải chứng minh những mệnh đề phụ thuộc vào số tự nhiên . Phương pháp quy nạp toán học là một trong những phương pháp rất hiệu quả để chứng minh những mệnh đề như vậy. | 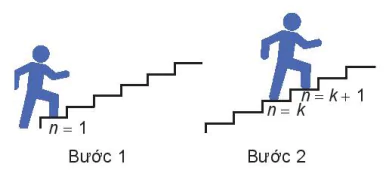 |
Bước 1: n = 1
Bước 2: n = k, n = k + 1
(Trang 26)
1. PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
>HĐ1. Hãy quan sát các đẳng thức sau:
1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
......
Có nhận xét gì về các số ở vế trái và ở vế phải của các đẳng thức trên? Từ đó hãy dự đoán công thức tính tổng của n số lẻ đầu tiên
1+3+5+...+(2n−1).
| >HĐ2. Xét đa thức p(n)=n2−n+41. a) Hãy tính p(1), p(2), p(3), p(4), p(5) và chứng tỏ rằng các kết quả nhận được đều là số nguyên tố. b) Hãy đưa ra một dự đoán cho p(n) trong trường hợp tổng quát. Chú ý. Khẳng định p(n) là số nguyên tố với mọi số tự nhiên n≥1 là một khẳng định sai. Mặc dù khẳng định này đúng với n=1,2,...,40, nhưng nó lại sai khi n=41. Thật vậy, với n=41 ta có p(41)=412 là hợp số (vì nó chia hết cho 41). |
Số nguyên tố là số tự nhiên lớn hơn 1 chỉ có hai ước số là 1 và chính nó. |
Để chứng minh tính đúng đắn của những mệnh đề phụ thuộc vào số tự nhiên n ∈ N* ta không thể thử trực tiếp với mọi số tự nhiên n ∈ N*. Tuy nhiên, ta có thể tiến hành như sau:
- Trước hết ta kiểm tra rằng mệnh đề là đúng với n = 1.
- Ta chứng minh rằng: từ giả thiết mệnh đề đúng với số tự nhiên n = k ≥ 1, suy ra nó cũng đúng với n = k+ 1.
Như thế mệnh đề là đúng với mọi số tự nhiên n ∈ N*
 |  |
| Phương pháp quy nạp toán học đôi khi được minh hoạ mô phỏng gắn liền với tác dụng tuần tự của hiệu ứng domino: Nếu - Quân domino đầu tiên bị đổ; - Mỗi quân domino đổ kéo theo quân domino kế tiếp bị đổ; thì tất cả các quân domino sẽ bị đổ. | |
Phương pháp lập luận trên đây gọi là phương pháp quy nạp toán học (thường gọi tắt là phương pháp quy nạp).
(Trang 27)
| Chứng minh một mệnh đề toán học phụ thuộc n ∈ N*, đúng với mọi n ∈ N*, bằng phương pháp quy nạp toán học, gồm hai bước sau: Bước 1. Kiểm tra rằng mệnh đề là đúng với n=1. Bước 2. Giả thiết mệnh đề đúng với số tự nhiên n=k≥1 (gọi là giả thiết quy nạp), chứng minh rằng mệnh đề đúng với n=k+1. Kết luận. |
| >Ví dụ 1. Chứng minh rằng với mọi số tự nhiên n≥1, ta có
|
Dùng phương pháp quy nạp để chứng minh công thức thu được sau dự đoán ở HĐ1. |
Giải
Ta chứng minh bằng quy nạp theo n.
Bước 1. Với n=1 ta có 1=12
Như vậy (1) đúng cho trường hợp n=1.
Bước 2. Giả sử (1) đúng với n=k, tức là ta có
1+3+5+7+...+(2k−1)=k2 → Giả thiết quy nạp
Ta sẽ chứng minh rằng (1) cũng đúng với n=k+1, nghĩa là ta sẽ chứng minh
1+3+5+7+...+(2k−1)+[2(k+1)−1]=(k+1)2.
Thật vậy, ta có
1 + 3 + 5 + 7 + ... + (2k - 1) + [2(k + 1) - 1] = [1 + 3 + 5 + 7 + ... + (2k - 1)] + (2k + 1)
= k2 + (2k + 1) → Theo giả thiết quy nạp
= k2 + 2k + 1 = (k + 1)2.
Vậy (1) đúng với mọi số tự nhiên n≥1.
>Luyện tập 1. Chứng minh rằng với mọi số tự nhiên n≥1, ta có
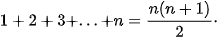
Chú ý. Nếu phải chứng minh một mệnh đề đúng với mọi số tự nhiên n≥p (p là một số tự nhiên nào đó) thì:
- Bước 1. Kiểm tra mệnh đề là đúng với n=p.
- Bước 2. Giả thiết mệnh đề đúng với số tự nhiên n=k ≥ p và chứng minh mệnh đề đúng với n=k+1. Kết luận.
>Ví dụ 2. Chứng minh rằng với mọi số tự nhiên n≥2, ta có đẳng thức
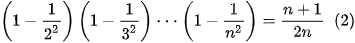
Giải. Ta chứng minh (2) bằng quy nạp theo n.
- Với n=2, ta có
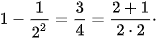 Như vậy (2) đúng với n=2.
Như vậy (2) đúng với n=2.
(Trang 28)
- Giả sử (2) đúng với n = k(k ≥ 2), tức là
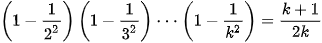
Ta sẽ chứng minh rằng công thức trên cũng đúng với n = k + 1, nghĩa là ta sẽ chứng minh
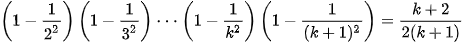
Thật vậy, sử dụng giả thiết quy nạp, ta có
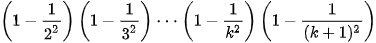
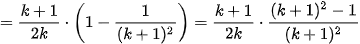
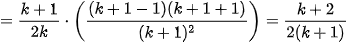
Vậy (2) đúng với mọi số tự nhiên n ≥ 2.
> Luyện tập 2. Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta có đằng thức
an - bn =(a-b)(an-1+an-2b+...+abn-2+bn-1).

ak+1- bk+1 = ak+1 - akb + akb - bk+1 =ak(a-b) + b(ak-bk).
2. MỘT SỐ ỨNG DỤNG KHÁC CỦA PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
Trong mục 1 ta đã sử dụng phương pháp quy nạp toán học để chứng minh một số đẳng thức phụ thuộc số tự nhiên n. Dưới đây ta xét một số ứng dụng khác của phương pháp quy nạp.
>Ví dụ 3. Chứng minh rằng với mọi số tự nhiên n,
n(n +1)(n+ 2) luôn chia hết cho 3. (3)
Giải
Ta chứng minh (3) bằng quy nạp theo n.
- Với n=0 ta có 0⋅(0+1)⋅(0+2)=0, chia hết cho 3.
Vậy (3) đúng với n=0.
- Giả sử (3) đúng với n=k, tức là
k(k+1)(k+2)⋮3,
ta cần chứng minh (3) đúng với n=k+1.
Từ giả thiết quy nạp ta suy ra k(k+1)(k+2)=3m, với m là số tự nhiên nào đó.
(Trang 29)
Khi đó ta có
(k+1)(k+2)(k+3) = (k+3)(k+1)(k+2) = k(k+1)(k+2)+3(k+1)(k+2)
= 3m+3(k+1)(k+2) = 3[m+(k+1)(k+2)], chia hết cho 3.
Vậy (3) đúng với mọi số tự nhiên n.
Nhận xét. Vì trong hai số tự nhiên liên tiếp luôn có một số chẵn nên từ kết quả của Ví dụ 3 suy ra: Tích của ba số tự nhiên liên tiếp luôn chia hết cho 6.
>Ví dụ 4. Chứng minh rằng với mọi số tự nhiên n≥3, ta có
2n > 2n+1. (4)
Giải
Ta chứng minh bất đẳng thức (4) bằng quy nạp theo n, với n≥3.
- Với n = 3 ta có 23 >7=2·3+1.
Vậy (4) đúng với n = 3.
- Giả sử (4) đúng với n = k ≥ 3, tức là ta có 2k > 2k +1.
Ta cần chứng minh (4) đúng với n = k + 1, tức là chứng minh 2k+1> 2(k +1)+1= 2k +3.
Thật vậy, theo giả thiết quy nạp, ta có
2k+1=2·2k>2·(2k +1) =4k+2=2k + 2(k +1)> 2k +3 do k ≥3.
Vậy bất đẳng thức (4) đúng với mọi số tự nhiên n≥3.
>Ví dụ 5. Sử dụng phương pháp quy nạp toán học, chứng minh rằng tổng các góc trong của một đa giác n cạnh (n≥3) là (n−2)⋅180°
| Giải. Ta chứng minh khẳng định trên bằng quy nạp theo n, với n≥3.
Thật vậy, xét đa giác k+1 cạnh A1A2...АkАk+1 nối hai đỉnh A1 và Ak ta được đa giác k cạnh A1A2...Аk. Theo giả thiết quy nạp, tổng các góc của đa giác k cạnh này bằng (k-2)-180°. Dễ thấy tổng các góc của đa giác A1A2...АkАk+1 bằng tổng các góc của đa giác A1A2...Аk, cộng với tổng các góc của tam giác Ak+1AkA1, tức là bằng (k-2).180°+180° =(k -1)·180° = [(k +1) -2]·180°. Vậy khẳng định đúng với mọi đa giác n cạnh, n ≥ 3. | 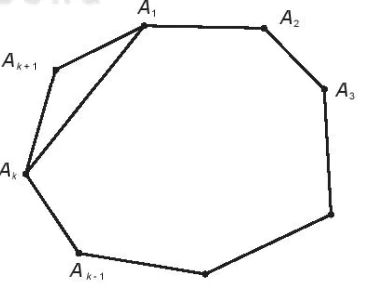 |
(Trang 30)
>Vận dụng (Công thức lãi kép)
Lãi suất gửi tiết kiệm trong ngân hàng thường được tính theo thể thức lãi kép theo định kì. Theo thể thức này, nếu đến kì hạn gửi người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp. Giả sử một người gửi số tiền A với lãi suất r không đổi trong mỗi kì.
a) Tính tổng số tiền (cả vốn lẫn lãi) T1, T2, T3 mà người đó nhận được sau kì thứ 1, sau kì thứ 2 và sau kì thứ 3.
b) Dự đoán công thức tính tổng số tiền (cả vốn lẫn lãi) Tn mà người đó thu được sau n kì. Hãy chứng minh công thức nhận được đó bằng quy nạp.
BÀI TẬP
2.1. Sử dụng phương pháp quy nạp toán học, chứng minh các đẳng thức sau đúng với mọi số tự nhiên n≥1.
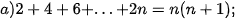
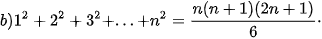
2.2. Mỗi khẳng định sau là đúng hay sai? Nếu em nghĩ là nó đúng, hãy chứng minh nó. Nếu em nghĩ là nó sai, hãy đưa ra một phản ví dụ.
a) p(n) = n² – n + 11 là số nguyên tố với mọi số tự nhiên n;
b) n²> n với mọi số tự nhiên n ≥ 2.
2.3. Chứng minh rằng n³- n + 3 chia hết cho 3 với mọi số tự nhiên n ≥ 1.
2.4. Chứng minh rằng n²- n + 41 là số lẻ với mọi số nguyên dương n.
2.5. Chứng minh rằng nếu x > -1 thi (1 + x)n ≥ 1+ nx với mọi số tự nhiên n.
2.6. Cho tổng 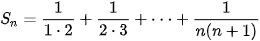
a) Tính S1, S2, S3.
b) Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.
2.7. Sử dụng phương pháp quy nạp toán học, chứng minh rằng số đường chéo của một đa giác n cạnh (n ≥ 4) là 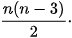
2.8. Ta sẽ 'lập luận” bằng quy nạp toán học đề chỉ ra rằng: “Mọi con mèo đều có cùng màu”. Ta gọi P(n) với n nguyên dương là mệnh đề sau: “Mọi con mèo trong một đàn gồm n con đều có cùng màu".
Bước 1. Với n = 1 thì mệnh đề P(1) là “Mọi con mèo trong một đàn gồm 1 con đều có cùng màu”. Hiển nhiên mệnh đề này là đúng!
Bước 2. Giả sử P(k) đúng với một số nguyên dương k nào đó. Xét một đàn mèo gồm k + 1 con. Gọi chúng là M1, M2,..., Mk+1 Bỏ con mèo Mk+1 ra khỏi đàn, ta nhận được một đàn mèo gồm k con là M1, M2,..., Mk. Theo giả thiết quy nạp, các con mèo có cùng màu.
(Trang 31)
Bây giờ, thay vì bỏ con mèo Mk+1, ta bỏ con mèo M1 để có đàn mèo gồm k con là M2, M3,... Mk+1. Vẫn theo giả thiết quy nạp thì các con mèo M2, M3,... Mk+1 có cùng màu. Cuối cùng, đưa con mèo M1, trở lại đàn đề có đàn mèo ban đầu. Theo các lập luận trên: các con mèo M1, M2,..., Mk có cùng màu và các con mèo M2, M3,... Mk+1 có cùng màu. Từ đó suy ra tắt cả các con mèo M1, M2,..., Mk+1 đều có cùng màu.
Vậy, theo nguyên lí quy nạp thì P(n) đúng với mọi số nguyên dương n. Nói riêng, nếu gọi N là số mèo hiện tại trên Trái Đất thì việc P(N) đúng cho thấy tất cả các con mèo (trên Trái Đất) đều có cùng màu!
Tất nhiên là ta có thể tìm được các con mèo khác màu nhau! Theo em thì "lập luận” trên đây sai ở chỗ nào?
| Em có biết? Phương pháp lập luận bằng quy nạp không phải là một phát minh của một cá nhân tại một thời điểm cố định nào. Người ta cho rằng các nhà toán học Hy Lạp đã biết tới nguyên lí quy nạp, nhưng không thật sự rõ ràng. Lập luận bằng quy nạp lần đầu tiên xuất hiện một cách tường minh trong cuốn sách Arithmeticorum Libri Duo năm 1575 của nhà toán học và thiên văn học người Ý Francesco Maurolico (1494 - 1575). Nhà toán học người Anh John Wallis (1616- 1703) được coi là người đầu tiên sử dụng thuật ngữ quy nạp. |

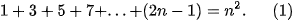






































































Bình Luận
Để Lại Bình Luận Của Bạn