Nội Dung Chính
(Trang 32)
| Thuật ngữ • Tam giác Pascal • Hệ số • Nhị thức Newton | Kiến thức, kĩ năng • Xác định các hệ số trong khai triển nhị thức Newton thông qua tam giác Pascal. • Khai triển nhị thức Newton (a+ b)n bằng cách sử dụng tam giác Pascal hoặc sử dụng công thức tổ hợp. • Xác định hệ số của x trong khai triền (ax+ b)n thành đa thức. |
Quan sát các khai triển nhị thức Newton sau:
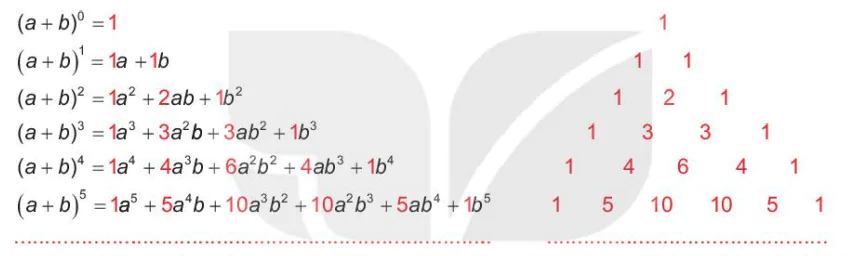
(a+b)0 =1
(a+b)1=1a +1b
(a+b)2 =1a² +2ab + 1b²
(a+b)3 =1a³ +3a²b+3ab² +1b3
(a+b)4 =1a4 +4a³b + 6a²b² + 4ab³ +1b4
(a+b)5 =1a5 + 5a4b +10a3b² +10a²b³ +5ab4 +1b5
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Các hệ số trong khai triền của (a + b)n tạo thành tam giác như ở hình trên. Có thể xác định được một hàng bất kì của tam giác này và do đó tính được các hệ số hay không?
1. TAM GIÁC PASCAL
>HĐ1. Khai triển (a + b)n, n ∈ {1; 2; 3; 4; 5}
Trong Bài 25 SGK Toán 10 (bộ sách Kết nối tri thức với cuộc sống), ta đã biết:
(a+b)1=a +b
(a+b)2 =a² +2ab + b²
(a+b)3 =a³ +3a²b+3ab² +b3
(a+b)4 =a4 +4a³b + 6a²b² + 4ab³ +b4
(a+b)5 =a5 + 5a4b +10a3b² +10a²b³ +5ab4 +b5
Với n ∈ {1; 2; 3; 4; 5}, trong khai triển của mỗi nhị thức (a + b)n:
a) Có bao nhiêu số hạng?
b) Tổng số mũ của a và b trong mỗi số hạng bằng bao nhiêu?
c) Số mũ của a và b thay đổi thế nào khi chuyền từ số hạng này đến số hạng tiếp theo, tính từ trái sang phải?
(Trang 33)
| Trong khai triển của (a + b)n (với n = 1, 2, 3, 4, 5):
|
Từ những quan sát này ta có thể dự đoán, chẳng hạn:
(a+b)6 = a6 +?a5b+?a4b2 +?a3b3 +? a2b4 + ?ab5 +b6.
Ở đây dấu “?" để chỉ các hệ số chưa biết. Để hoàn thành khai triển, ta cần xác định các hệ số này.
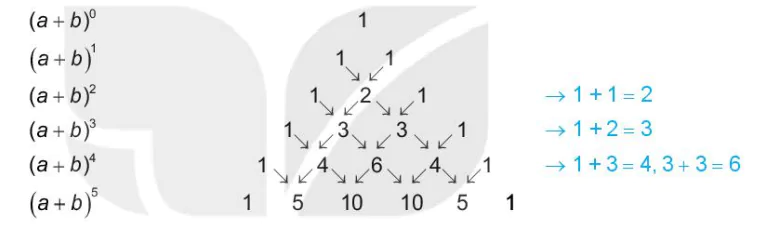
>HĐ2. Tam giác Pascal
Viết các hệ số của khai triền (a + b)n với một số giá trị đầu tiên của n, trong bằng tam giác sau đây, gọi là tam giác Pascal
(a+b)0
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
→1+1= 2
→1+2=3
→1+3=4,3+3=6
Hàng đầu quy ước gọi là hàng 0. Hàng n ứng với các hệ số trong khai triền nhị thức (a + b)n.
| Trong tam giác Pascal: Mọi số (khác 1) đều là tổng của hai số ở ngay phía trên nó. |
Từ tính chất này ta có thể tìm bất kì hàng nào của tam giác Pascal từ hàng ở ngay phía trên nó. Chằng hạn ta có thể tìm hàng 6 từ hàng 5 như sau:

(a+b)5
(a+b)6
1 5 10 10 5 1
1 6 15 20 15 6 1
→1+5= 6,5+ 10= 15, 10+ 10 = 20
? Tìm các hàng 7 và 8 của tam giác Pascal.
>Ví dụ 1. Sử dụng tam giác Pascal viết khai triển của (a+b)6.
Giải
Khai triển của (a+b)6 có dạng
(a+b)6 = a6 + ?a5b +?a4b2 + ?a3b3 + ?a2b4 + ?ab5 + b6
Các hệ số trong khai triễn này là các hệ số ở hàng 6 của tam giác Pascal. Do đó ta có ngay
(a+b)6 = a6 + 6a5b +15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6
(Trang 34)
>Ví dụ 2. Sử dụng tam giác Pascal viết khai triển của (3 - 2x)5.
Giải
Ta viết khai triển của (a+b)5 rồi sau đó thay a = 3, b = -2x vào khai triển nhận được.
Dựa vào hàng 5 của tam giác Pascal, ta có
(a+b)5 =a5 + 5a4b +10a3b² +10a²b³ +5ab4 +b5
Với a = 3, b = -2x, ta được
(3 - 2x)5 = 35 + 5·34(-2x) + 10·33(-2x)2 + 10·32(-2x)3 +5·3(-2x)4 + (-2x)5
=243 - 810x + 1080x2 - 720x3 + 240x4 - 32x5.
>Luyện tập 1.
a) Sử dụng tam giác Pascal viết khai triển của (a+ b)7.
b) Sử dụng tam giác Pascal viết khai triền của (2х - 1)4.
Dưới đây ta sẽ xây dựng công thức cho phép xác định trực tiếp hệ số bất kì trong khai triển (a + b)n.
>HĐ3. Tính chất của các số 
a) Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo mẫu:
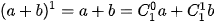
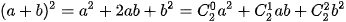
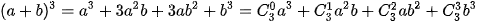
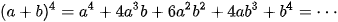
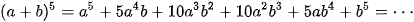
Nhận xét rằng các hệ số khai triền của hai số hạng cách đều số hạng đầu và số hạng cuối luôn bằng nhau. Hãy so sánh, chẳng hạn, 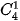 và
và 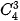
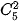 và
và 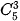 . Từ đó hãy dự đoán hệ thức giữa
. Từ đó hãy dự đoán hệ thức giữa 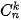 và
và 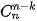 (0 ≤k≤n).
(0 ≤k≤n). b) Dựa vào kết quả của HĐ3a, ta có thể viết những hàng đầu của tam giác Pascal dưới dạng:
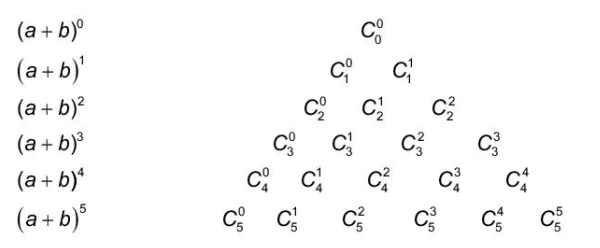
(a+b)0
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5

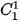
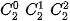
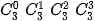
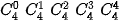
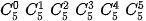
Từ tính chất của tam giác Pascal, hãy so sánh  +
+ 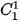 và
và 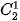
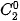 +
+ 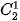 và
và 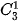 ,... Từ đó hãy dự đoán hệ thức giữa
,... Từ đó hãy dự đoán hệ thức giữa 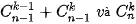 .
. (Trang 35)
| Tính chất của các số • • |
? Hãy chứng minh các công thức trên bằng cách sử dụng công thức tính số các tổ hợp.
2. CÔNG THỨC NHỊ THỨC NEWTON
>HĐ4. Quan sát khai triền nhị thức của (a + b)n n ∈ {1; 2; 3; 4; 5} ở HĐ3, hãy dự đoán công thức khai triền trong trường hợp tổng quát.
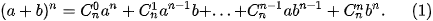 |
Chứng minh
Ta chứng minh (1) bằng quy nạp theo n.
• Khi n = 1, ta có
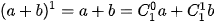
Vậy công thức (1) đúng khi n = 1.
• Giả sử (1) là đúng với n = m, tức là ta có
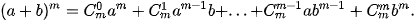
Ta sẽ chứng minh rằng (1) cũng đúng khi n = m + 1, tức là
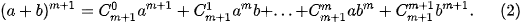
Thật vậy, ta có
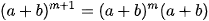
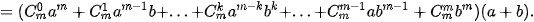
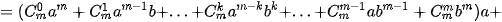
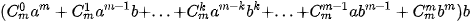
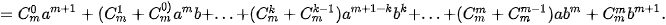
Vì 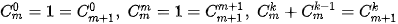
Vậy công thức nhị thức Newton là đúng với mọi số nguyên dương n.
Chú ý. Số hạng thứ (k + 1) trong khai triền của(a + b)n thành dạng (1) là 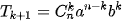
>Ví dụ 3. Viết khai triển nhị thức Newton (a+ b)6.
Giải
Ta có
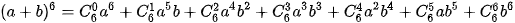
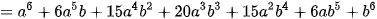
Như vậy, ta tìm lại được kết quả của Ví dụ 1, nhưng bằng phương pháp khác.
(Trang 36)
Chú ý. Vì 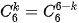 (0≤ k ≤ 6) nên ta chỉ cần tính
(0≤ k ≤ 6) nên ta chỉ cần tính 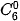
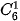 ,
, 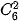 ,
, 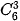 và dùng tính chất này để suy ra
và dùng tính chất này để suy ra 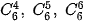
>Ví dụ 4. Khai triển biểu thức (3x – 2)4.
Giải
Theo công thức nhị thức Newton, ta có
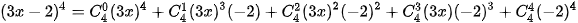
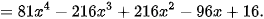
>Luyện tập 2. Khai triển (x-2y)6.
Số hạng chứa xk trong khai triền của (ax + b)n là 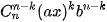 hay hay 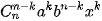 . Do đó, hệ số của xk trong khai triển của (ax + b)n là . Do đó, hệ số của xk trong khai triển của (ax + b)n là 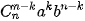 . . |
>Ví dụ 5. Tìm hệ số của x⁴ trong khai triền của (x + 2)10.
Giải. Số hạng chứa xk trong khai triền của (x + 2)10 là 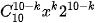
Số hạng chứa x⁴ ứng với k = 4, tức là số hạng 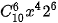 hay 13 440x⁴.
hay 13 440x⁴.
Vậy hệ số của x⁴ trong khai triền của (x + 2)10 là 13 440.
>Luyện tập 3. Tìm hệ số của x7 trong khai triển thành đa thức của (2 - 3x)10.
>Ví dụ 6. Tìm số nguyên dương n thoả mãn
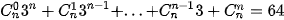
Giải. Nhận thấy về trái của đằng thức trên có chứa các luỹ thừa của 3 nên áp dụng khai triển nhị thức Newton cho (x + 3)n ta được
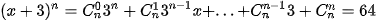
Cho x = 1 ta được
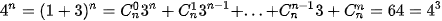
Vậy số nguyên dương cần tìm là n = 3.
>Vận dụng (Số các tập con của tập hợp có n phần từ)
a) Viết khai triền nhị thức Newton của (1 + x)n.
b) Cho x = 1 trong khai triền ở câu a), viết đẳng thức nhận được. Giải thích ý nghĩa của đằng thức này với lưu ý rằng 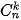
c) Tương tự, cho x = -1 trong khai triển ở câu a), viết đằng thức nhận được. Giải thích ý nghĩa của đằng thức này.
(Trang 37)
BÀI TẬP
2.9. Sử dụng tam giác Pascal, viết khai triển:
a) (x- 1)5; b) (2x-3y)4.
2.10. Viết khai triển theo nhị thức Newton:
a) (x+y)6; b) (1-2x)5.
2.11. Tìm hệ số của x8 trong khai triền của (2x + 3)10.
2.12. Biết hệ số của x² trong khai triển của (1 - 3x)n là 90. Tìm n.
2.13. Từ khai triền biểu thức (3x – 5)4 thành đa thức, hãy tính tổng các hệ số của đa thức nhận được.
2.14. Tìm hệ số của x5 trong khai triển thành đa thức của biều thức
x(1-2x)5 + x2 (1+3x)10.
2.15. Tính tổng sau đây:
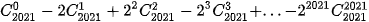
2.16. Tìm số tự nhiên n thoả mãn
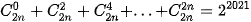
2.17. Tim số nguyên dương n sao cho
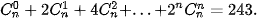
2.18. Biết rằng (2+x)100 = a0 +a1x+a₂x² +..+ a100x100. Với giá trị nào của k (0 ≤ k ≤ 100) thì ak lớn nhất?
Em có biết?
|
Blaise Pascal (1623-1662) |
|
Isaac Newton (1643-1727) |
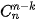 (0 ≤k ≤ n) (Tính chất đối xứng).
(0 ≤k ≤ n) (Tính chất đối xứng).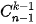 +
+ 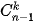 =
= 





































































Bình Luận
Để Lại Bình Luận Của Bạn