(Trang 39)
| Thuật ngữ
| Kiến thức, kĩ năng
|
| Mỗi hành tinh trong Hệ Mặt Trời chuyển động theo một quỹ đạo hình elip nhận tâm Mặt Trời là một tiêu điểm. Khoảng cách lớn nhất và nhỏ nhất từ Trái Đất đến tâm Mặt Trời tương ứng khoảng 152⋅106 km và 147⋅106 km (theo nssdc.gsfc.nasa.gov). Liệu có lập được phương trình chính tắc của elip là quỹ đạo của Trái Đất? |  |
(Trang 40)
1. HÌNH DẠNG CỦA ELIP
>HĐ1. Cho elip có phương trình chính tắc 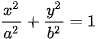 (H.3.1).
(H.3.1).
| a) Tìm toạ độ các giao điềm của elip với các trục toạ độ. b) Hãy giải thích vì sao, nếu điểm M(x0; y0) thuộc elip thì các điềm có toạ độ ((x0; -y0), (-x0; y0), (-x0; -y0 )cũng thuộc elip. c) Với điểm M(x0; y0) thuộc elip, hãy so sánh OM2 với a2, b2. |
Hình 3.1 |
| Cho elip có phương trình chính tắc
|
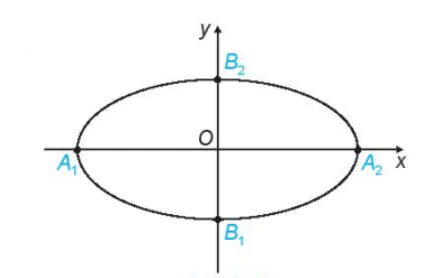
>Ví dụ 1. Cho elip 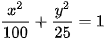 . Tính độ đài các trục B2 và toạ độ các đỉnh của elip đó.
. Tính độ đài các trục B2 và toạ độ các đỉnh của elip đó.
| Giải Các trục lớn, trục nhỏ của elip tương ứng (H.3.2) có độ dài Do đó, elip có các đỉnh là A1(-10; 0), A2(10; 0), B1(0; -5), B2(0; 5). |
Hình 3.2 |
>Luyện tập 1. Viết phương trình chính tắc của elip với độ dài trục lớn bằng 10 và tiêu cự bằng 6.
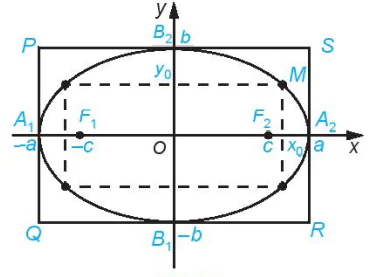
>Ví dụ 2. Cho elip có phương trình chính tắc 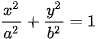 . Chứng minh rằng, các điểm thuộc elip và khác đỉnh đều nằm trong hình chữ nhật cơ sở, còn bốn đỉnh của elip là trung điểm của các cạnh của hình chữ nhật đó.
. Chứng minh rằng, các điểm thuộc elip và khác đỉnh đều nằm trong hình chữ nhật cơ sở, còn bốn đỉnh của elip là trung điểm của các cạnh của hình chữ nhật đó.
(Trang 41)
Giải
Gọi M(x0; y0) là một điểm thuộc elip. Do 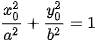 nên
nên 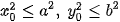 và nếu
và nếu 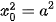
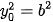 thì x0 = 0. Vậy hoặc –a<x0<a, -b<y0<b hoặc cặp (x0; y0) là một trong bốn cặp (-a; 0), (a; 0), (0; -b), (0; b). Từ đó, ta có điều phải chứng minh.
thì x0 = 0. Vậy hoặc –a<x0<a, -b<y0<b hoặc cặp (x0; y0) là một trong bốn cặp (-a; 0), (a; 0), (0; -b), (0; b). Từ đó, ta có điều phải chứng minh.
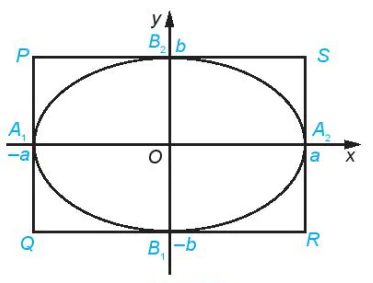
Hình 3.3
Chú ý
Khi tỉ số 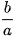 càng nhỏ (càng gần về 0), thì hình chữ nhật cơ sở càng "dẹt" và elip càng "gầy".
càng nhỏ (càng gần về 0), thì hình chữ nhật cơ sở càng "dẹt" và elip càng "gầy".
Khi tỉ số 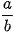 càng lớn (càng gần tới 1), thì hình chữ nhật cơ sở càng gần với hình vuông và elip càng "béo" (càng gần đường tròn) (H.3.4).
càng lớn (càng gần tới 1), thì hình chữ nhật cơ sở càng gần với hình vuông và elip càng "béo" (càng gần đường tròn) (H.3.4).
|
|
|
|
Hình 3.4
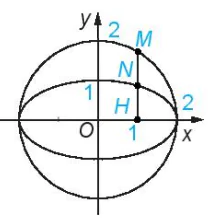
>Luyện tập 2. (Phép co đường tròn). Cho đường tròn có phương trình x² + y² = a² và số k (0 < k< 1). Với mỗi điểm M(x0; y0) thuộc đường tròn, gọi H(x0; 0) là hình chiều vuông góc của M lên trục Ox và N là điểm thuộc đoạn MH sao cho HN = kHM (H.3.5).
a) Tính toạ độ của N theo x0; y0; k.
b) Chứng minh rằng khi điểm M thay đổi trên đường tròn thì N thay đổi trên elip có phương trình chính tắc 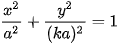 .
.
(Trang 42)
| Chú ý Người ta nói: Phép co về trục hoành hệ số k biến đường tròn x²+ y²= a² thành elip có phương trình |
Hình 3.5 |
2. BÁN KÍNH QUA TIÊU, TÂM SAI VÀ ĐƯỜNG CHUẨN
> HĐ2. Cho elip có hai tiêu điểm F1(-c; 0), F2(c; 0) và độ dài trục lớn bằng 2a và điềm M(x; у).
a) Tính 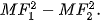
b) Khi điểm M thuộc elip 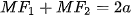
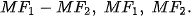
Cho elip có phương trình chính tắc 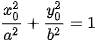 , với các tiêu điểm F1(-c; 0), F2(c; 0) (với , với các tiêu điểm F1(-c; 0), F2(c; 0) (với 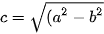 ). Với điểm M(x; y) thuộc elip, ta có ). Với điểm M(x; y) thuộc elip, ta có 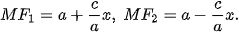 Các đoạn thằng MF1, MF2 được gọi là bán kính qua tiêu của M. Các đoạn thằng MF1, MF2 được gọi là bán kính qua tiêu của M. |
>Ví dụ 3. Cho elip có phương trình chính tắc 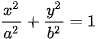
Giải. Elip có nửa tiêu cự là 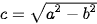 . Với mỗi điểm M(x0; y0) thuộc elip, ta có bán kính qua tiêu của M ứng với tiêu điểm F1 là
. Với mỗi điểm M(x0; y0) thuộc elip, ta có bán kính qua tiêu của M ứng với tiêu điểm F1 là 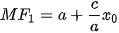 . Mặt khác M(x0; y0) thuộc elip nên
. Mặt khác M(x0; y0) thuộc elip nên 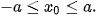 Do đó,
Do đó, 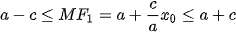 . Hơn nữa,
. Hơn nữa, 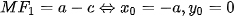
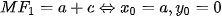 . Vậy MF1 nhỏ nhất khi điềm M trùng đình A1(-a; 0) và MF1 lớn nhất khi điềm M trùng đỉnh A2(a; 0) của elip.
. Vậy MF1 nhỏ nhất khi điềm M trùng đình A1(-a; 0) và MF1 lớn nhất khi điềm M trùng đỉnh A2(a; 0) của elip. Chú ý
Tương tự Ví dụ 3, khoảng cách từ M đến tiêu điểm F2 là nhỏ nhất khi M trùng đỉnh A2(a; 0) và lớn nhất khi M trùng đỉnh A1(-a; 0).

Bán kính qua tiêu có độ dài lớn nhất bằng nửa tổng của độ dài trục lớn và tiêu cự, và có độ dài nhỏ nhất bằng nửa hiệu của độ dài trục lớn và tiêu cự.
>Luyện tập 3. Cho elip 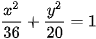 , điểm M thay đổi trên elip. Hỏi khoảng cách từ M tới một tiêu điểm của elip lớn nhất bằng bao nhiêu, nhỏ nhất bằng bao nhiêu?
, điểm M thay đổi trên elip. Hỏi khoảng cách từ M tới một tiêu điểm của elip lớn nhất bằng bao nhiêu, nhỏ nhất bằng bao nhiêu?
(Trang 43)
>Vận dụng 1. Với thông tin được đưa ra trong tình huống mở đầu, lập phương trình chính tắc của elip quỹ đạo của Trái Đất, với 1 đơn vị đo trên mặt phẳng toạ độ ứng với 106 km trên thực tế.
>HĐ3. Cho ellp có phương trình chính tắc 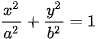 , với các tiêu điểm F1(-c; 0), F2(c; 0), ở đây
, với các tiêu điểm F1(-c; 0), F2(c; 0), ở đây 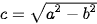
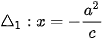 và
và 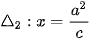 .
. Với điểm M(x; y) thuộc elip, tính các tỉ số 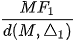 và
và  theo a và c.
theo a và c.
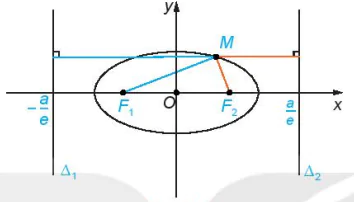
Hình 3.6
| Cho ellp có phương trình chính tắc Khi điểm M(x; y) thay đổi trên elip, ta luôn có
|
Chú ý
- Tâm sai e của elip là một số dương nhỏ hơn 1.
- Độ dài các bán kính qua tiêu của điểm M(x; y) thuộc elip còn được viết dưới dạng
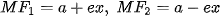 .
.
>Ví dụ 4. Cho elip 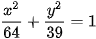 . Tim tâm sai, tiêu điềm và các đường chuần của elip.
. Tim tâm sai, tiêu điềm và các đường chuần của elip.
Giải
Ta có a2 = 64, b2 = 39. Suy ra a = 8, 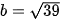 và
và 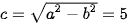
Vậy elip có hai tiêu điềm là F1(-5; 0), F2(5; 0) và tâm sai là 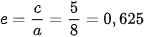 . Đường chuẩn ứng với tiêu điểm F1 là
. Đường chuẩn ứng với tiêu điểm F1 là  và đường chuần ứng với tiêu điểm F2 là
và đường chuần ứng với tiêu điểm F2 là 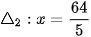 .
.
(Trang 44)
>Luyện tập 4. Cho elip có phương trình chính tắc 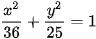 . Tìm tâm sai và các đường chuần 36 25 của elip. Tính các bán kính qua tiêu của điểm M thuộc elip và có hoành độ bằng -2.
. Tìm tâm sai và các đường chuần 36 25 của elip. Tính các bán kính qua tiêu của điểm M thuộc elip và có hoành độ bằng -2.
Nhận xét. Trong phương trình chính tắc của elip, vì tâm sai 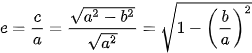
- e càng nhỏ (càng gần về 0) thì
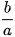 càng lớn và do đó elip càng “béo" (càng gần đường tròn);
càng lớn và do đó elip càng “béo" (càng gần đường tròn); - e càng lớn (càng gần tới 1) thì
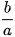 càng nhỏ và do đó elip càng "dẹt" (H.3.7).
càng nhỏ và do đó elip càng "dẹt" (H.3.7).
|
e= 0,1 |
e = 0,5 |
e = 0,68 |
e= 0,86 |
Hình 3.7
>Vận dụng 2. Mặt Trăng chuyền động theo một quỹ đạo hình elip nhận tâm Trái Đất là một tiêu điềm. Các khoảng cách lớn nhất và nhỏ nhất từ các vị trí của Mặt Trăng đến tâm Trái Đất tương ứng là 400 000 km và 363 000 km (theo nssdc.gsfc.nasa.gov). Tìm tâm sai của quỹ đạo elip.
BÀI TẬP
3.1. Cho elip 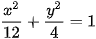
a) Xác định các đỉnh và độ dài các trục của elip.
b) Xác định tâm sai và các đường chuần của elip.
c) Tính các bán kính qua tiêu của điềm M thuộc elip, biết điềm M có hoành độ bằng -3.
3.2. Viết phương trình chính tắc của elip trong mỗi trường hợp sau:
a) Độ dài trục lớn bằng 8, tiêu cự bằng 6;
b) Độ dài trục lớn bằng 8 và tâm sai bằng 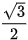
3.3. Cho elip 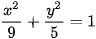
a) Qua tiêu điềm của elip vẽ đường thẳng vuông góc với trục Ox, cắt elip tại hai điểm A và B. Tính độ dài đoạn thẳng AB.
b) Tìm điểm M trên elip sao cho MF1 = 2MF2 với F1 và F2 là hai tiêu điểm của elip (hoành độ của F1 âm).
(Trang 45)
3.4. Đường tròn phụ của hình elip là đường tròn có đường kính là trục nhỏ của elip (H.3.8). Do đó, đường tròn phụ là đường tròn lớn nhất có thể nằm bên trong một hình elip. Tim phương trình đường tròn phụ của elip 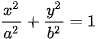
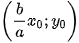 thuộc đường tròn phụ.
thuộc đường tròn phụ. 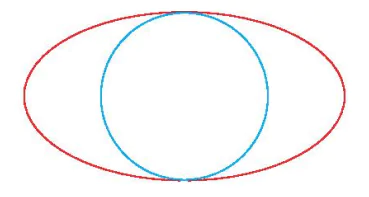
Hình 3.8
3.5. Với tâm sai khoảng 0,244, quỹ đạo elip của sao Diêm Vương “dęt" hơn so với quỹ đạo của tám hành tinh trong hệ Mặt Trời (xem Em có biết? ở cuối bài). Nửa độ dài trục lớn của elip quỹ đạo là khoảng 590 635-106 km. Tìm khoảng cách gần nhất và khoảng cách xa nhất giữa sao Diêm Vương và tâm Mặt Trời (tiêu điểm của quỹ đạo) (theo nssdc.gsfc.nasa.gov).
3.6. Một phòng thì thầm có trần vòm elip với hai tiêu điểm ở độ cao 1,6 m (so với mặt sàn) và cách nhau 1,6 m. Đỉnh của mái vòm cao 7,6 m (H.3.9). Hỏi âm thanh thì thầm từ một tiêu điểm thì sau bao nhiêu giây đến được tiêu điểm kia? Biết vận tốc âm thanh là 343,2m/s và làm tròn đáp số tới 4 chữ số sau dấu phẩy.
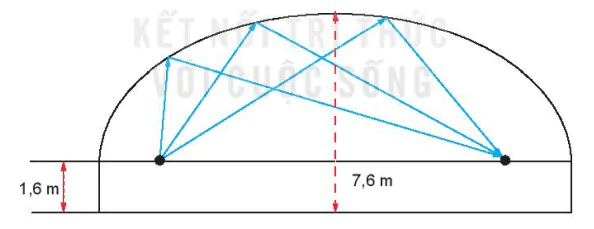
Hình 3.9
| Em có biết?
|
(Trang 46)
Sau Kepler khoảng tám thập kỉ, Newton đã chỉ ra rằng, các định luật về chuyền động và Định luật vạn vật hấp dẫn của ông kéo theo ba định luật nói trên của Kepler. |
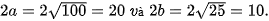

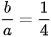

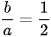
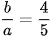
 không đổi, trong đó
không đổi, trong đó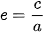 được gọi là tâm sai của elip.
được gọi là tâm sai của elip.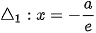
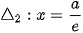 được gọi là các đường chuần tương ứng với F1 và F2 của elip.
được gọi là các đường chuần tương ứng với F1 và F2 của elip.









































































Bình Luận
Để Lại Bình Luận Của Bạn