Nội Dung Chính
(Trang 38)
2.19. Chứng minh rằng với mọi số tự nhiên n ≥ 1, ta có
2·21 + 3·22 + 4·23 +...+ (n +1)·2n = n·2n+1
2.20. Đặt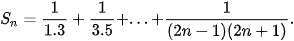 
a) Tính S1, S2, S3.
b) Dự đoán công thức tính tổng Sn và chứng minh nó bằng quy nạp.
2.21. Chứng minh rằng với mọi số tự nhiên n, ta có 102n-1 + 1 chia hết cho 11.
2.22. Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta có
5n ≥ 3n + 4n.
2.23. a) Khai triển (1 + x)10. b) So sánh (1, 1)10 và 2.
2.24. Tìm hệ số của x9 trong khai triển thành đa thức của (2x-3)11.
2.25. Khai triển đa thức (1 + 2x)12 thành dạng a0 + a1x + a2x2 +...+ a12x12
Tìm hệ số ak lớn nhất.
2.26. Chứng minh rằng
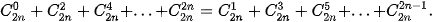
Áp dụng: Tìm số nguyên dương n thoả mãn
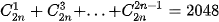
2.27. Tim giá trị lớn nhất trong các giá trị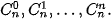 
Áp dụng: Tìm hệ số lớn nhất của khai triền (a + b)n, biết rằng tổng các hệ số của khai triển bằng 4 096.
2.28. Tìm số hạng có giá trị lớn nhất của khai triển (p + q)n với p> 0, q> 0, p+ q = 1.
Các Bài Học Khác
Chuyên đề học tập Toán 10 - Bài 4: Nhị Thức Newton - Nắm vững công thức, tính chất và ứng dụng để khai triển biểu thức, giải các bài toán tổ hợp phức tạp một cách hiệu quả.
Xem thêm ⟶
Chuyên đề học tập Toán 10 - Bài 3: Phương Pháp Quy Nạp Toán Học - Nắm vững các bước chứng minh mệnh đề và vận dụng để giải quyết một số vấn đề thực tiễn.
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn