CHƯƠNG I. TẬP HỢP CÁC SỐ TỰ NHIÊN
(SỐ HỌC)
Khi tính toán với những số nhỏ, người xưa chỉ cần dùng đến các ngón tay. Nhưng khi gặp các số lớn thì sao? Các hệ đếm xuất hiện để giúp con người tính toán với những số lớn. Chương này sẽ giúp các em làm quen hệ (đếm) thập phân để biểu diễn và tính toán với các số tự nhiên. Thật dễ dàng và thuận tiện!
BÀI 1. TẬP HỢP
KHÁI NIỆM, THUẬT NGỮTập hợp, phần tử
| KIẾN THỨC, KĨ NĂNG• Nhận biết một tập hợp và các phần tử của nó. • Mô tả một tập hợp (cho một tập hợp). • Sử dụng kí hiệu và cách diễn đạt toán học nhờ tập hợp. |
|
Tập hợp gồm các bông hồng trong lọ hoa Hình 1.1 |
Tập hợp gồm ba con cá vàng trong bình Hình 1.2 |
Bài này sẽ giúp các em tìm hiểu về tập hợp, một khái niệm cơ bản của Toán học.
1. TẬP HỢP VÀ PHẦN TỬ CỦA TẬP HỢP
Tập hợp
- Trên Hình 1.1 (H 1.1) ta có tập hợp các bông hồng trong lọ hoa.
- Trên Hình 1.2 ta có tập hợp các con cá vàng trong bình cá.
- Hình 1.3 biểu diễn tập hợp gồm các số 4; 1; 9 và 8. Nếu kí hiệu M là tập hợp này thì các số 4; 1; 9 và 8 là các phần tử của tập hợp M.
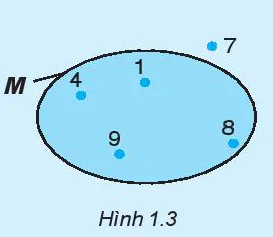
Hình 1.3
- Gọi B là tập hợp các chữ các viết thường trong tiếng Việt. Khi đó a, b, c,... là những phần tử của tập hợp B.
| Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định. Các đối tượng ấy được gọi là những phần tử của tập hợp. x là một phần tử của tập hợp A, kí hiệu x ∈ A (đọc là x thuộc A). y không là một phần tử của tập hợp A. Kí hiệu y ∉ A (đọc là y không thuộc A). |
Chú ý. Khi x thuộc A, ta còn nói “x nằm trong A”, hay “A chứa x”.
Người ta thường đặt tên tập hợp bằng chữ cái in hoa.
Ví dụ
Với tập hợp M trên Hình 1.3, ta có 4 ∈ M, 1 ∈ M, 7 ∉ M.
Luyện tập 1
Gọi B là tập hợp các bạn tổ trưởng trong lớp em.
Em hãy chỉ ra một bạn thuộc tập B và một bạn không thuộc tập B.
2. MÔ TẢ MỘT TẬP HỢP
Mô tả một tập hợp là cho biết cách xác định các phần tử của tập hợp đó. Ta thường dùng hai cách mô tả tập hợp sau:
Hai cách mô tả một tập hợp
Cách 1. Liệt kê các phần tử của tập hợp, tức là viết các phần tử của tập hợp trong dấu ngoặc { } theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.
Ví dụ, với tập P gồm các số 0; 1; 2; 3; 4; 5 ở Hình 1.4, ta viết:
P = {0; 1; 2; 3; 4; 5}
Cách 2. Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp
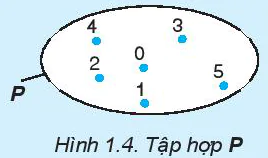
Hình 1.4. Tập hợp P
Ví dụ, với tập P (xem H 1.4) ta cũng có thể viết:
P = {n | ℕ n là số tự nhiên nhỏ hơn 6}
Câu hỏi: Khi mô tả tập hợp L các chữ cái trong từ NHA TRANG bằng cách liệt kê các phần tử, bạn Nam viết:
L = {N; H; A; T; R; A; N; G}
Theo em, bạn Nam viết đúng hay sai?
Ta viết các phần tử của một tập hợp cách nhau bởi dấu ";".
Chú ý:
1. Gọi ℕ là tập hợp gồm các số tự nhiên 1, 2, 3;... Ta có thể viết tập ℕ như sau: ℕ = {0; 1; 2; 3;...}.
2. Ta viết n ∈ ℕ có nghĩa n là một số tự nhiên. Chẳng hạn, tập P các số tự nhiên nhỏ hơn 6 có thể viết là:
P = {n | n ∈ ℕ, n < 6} hoặc P = {n ∈ ℕ | n < 6}
3. Ta còn dùng kí hiệu ℕ* để chỉ tập hợp các số tự nhiên khác 0, nghĩa là ℕ* = {1; 2; 3;... }
Luyện tập 2
Viết các tập hợp sau bằng cách liệt kê các phần tử của chúng:
A = {x ∈ ℕ | x < 5};
B = {x ∈ ℕ* | x < 5}.ℕ*
Luyện tập 3
Gọi M là tập hợp các số tự nhiên lớn hơn 6 và nhỏ hơn 10.
a) Thay dấu “?” bằng dấu ∈ hoặc ∉: 5 ? M; 9 ? M.
b) Mô tả tập hợp M bằng hai cách.
BÀI TẬP
1.1. Cho hai tập hợp:
A = {a; b; c; x; y} và B = {b; d; y; t; u; v}.
Dùng kí hiệu “∈” hoặc “∉” để trả lời các câu hỏi: Mỗi phần tử a, b, x, u thuộc tập nào và không thuộc tập hợp nào?
1.2. Cho tập hợp
U = {x ∈ ℕ | x chia hết cho 3}.
Trong các số 3; 5; 6; 0; 7 số nào thuộc và số nào không thuộc tập hợp U?
1.3. Bằng cách liệt kê các phần tử, hãy viết các tập hợp sau:
a) Tập hợp K các số tự nhiên nhỏ hơn 7;
b) Tập hợp D tên các tháng (dương lịch) có 30 ngày;
c) Tập hợp M các chữ cái tiếng Việt trong từ “ĐIỆN BIÊN PHỦ”.
1.4. Bằng cách nêu dấu hiệu đặc trưng, hãy viết tập hợp A các số tự nhiên nhỏ hơn 10.
1.5. Viết các tập hợp sau bằng cách liệt kê các phần tử của chúng:
A = {x ∈ ℕ | x < 5};
B = {x ∈ ℕ* | x < 5}.
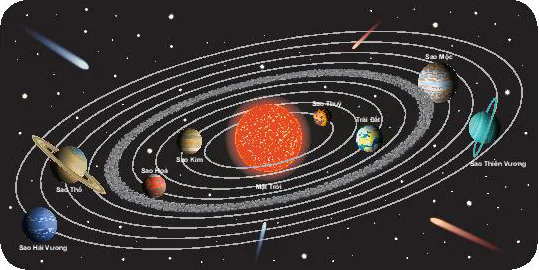
1.6. Hệ Mặt Trời gồm có Mặt Trời ở trung tâm và 8 thiên thể quay quanh Mặt Trời gọi là các hành tinh, đó là Thủy Tinh, Kim tinh, Trái Đất, Hỏa tinh, Mộc tinh, Thổ tinh, Thiên Vương tinh và Hải Vương tinh. Gọi S là tập các hành tinh của Hệ Mặt Trời. Hãy viết tập S bằng cách liệt kê các phần tử của S.
EM CÓ BIẾT?
Nhà toàn học Cantor

Georg Cantor
(1845 - 1918)
Con người biết đến toán học từ hàng nghìn năm trước Công nguyên. Nhưng mãi đến cuối thế kỉ XIX, Ií thuyết tập hợp mới được phát triển nhờ các nghiên cứu của nhà toán học Cantor (Căng-to), người Đức. Từ đó lí thuyết tập hợp đã nhanh chóng trở thành nền tảng của Toán học hiện đại.
Tập hữu hạn và tập vô hạn
Ta thấy:
Tập X= {x; y} có 2 phần tử;
Tập Y= {1; 2; 3;... ; 50} có 50 phần tử. X và Y là những tập hợp có một số hữu hạn phần tử. Ta gọi chúng là những tập hữu hạn.
Khác với tập X, Y, tập hợp có vô số phần tử là tập vô hạn. Tập N là tập vô hạn.
Giao của hai tập hợp
Gọi C là tập hợp gồm các phần tử chung của hai tập A và B.
Ta gọi tập C là giao của hai tập A và B, kí hiệu C = A ∩ B.













































Bình Luận
Để Lại Bình Luận Của Bạn