Nội Dung Chính
KHÁI NIỆM, THUẬT NGỮLũy thừa Cơ số; Số mũ Bình phương; Lập phương | KIẾN THỨC, KĨ NĂNG• Thực hiện phép tính nâng lên lũy thừa với số mũ tự nhiên. • Nhân, chia hai lũy thừa cùng cơ số với số mũ tự nhiên. • Giải quyết được những vấn đề thực tiễn gắn với thực hiện phép tính lũy thừa với số mũ tự nhiên. |
Truyền thuyết Ấn Độ kể rằng, người phát minh ra bàn cờ vua đã chọn phần thưởng là số thóc rải trên 64 ô của bàn cờ vua như sau: ô thứ nhất để 1 hạt thóc, ô thứ hai để 2 hạt, ô thứ ba để 4 hạt, ô thứ tư để 8 hạt,… Cứ như thế, số hạt ở ô sau gấp đôi số hạt ở ô trước.
Liệu nhà vua có đủ thóc để thưởng cho nhà phát minh đó hay không?

Bàn cờ vua
1. LŨY THỪA VỚI SỐ MŨ TỰ NHIÊN
Phép nhân lũy thừa
Bảng sau đây chỉ ra cách tính số hạt thóc ở một số ô trong bàn cờ trong bài toán mở đầu:
| Ô thứ | Phép tính tìm số hạt thóc | Số hạt thóc |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 2 . 2 | 4 |
| 4 | 2 . 2 . 2 | 8 |
| 5 | 2 . 2 . 2 . 2 | 16 |
| ... | ... | ... |
HĐ1 Để tìm số hạt thóc ở ô thứ 8, ta phải thực hiện phép nhân có bao nhiêu thừa số 2?
Lũy thừa bậc n của số tự nhiên a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
an = a . a . ... . a (n ∈ ℕ*)
a . a . ... . a (n thừa số)
an đọc là “a mũ n” hoặc “ a lũy thừa n”, a là cơ số, n là số mũ.
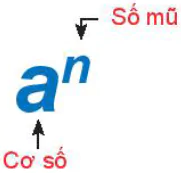
an
n: Số mũ; a: Cơ số
| Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên luỹ thừa. |
Chú ý. Ta có a1 = a.
a2 cũng được gọi là a bình phương (hay bình phương của a);
a3 cũng được gọi là a lập phương (hay lập phương của a).
Các số 0, 1, 4, 9, 16,... gọi là các số chính phương. 12 22 32 42

Ví dụ 1
a) Viết biểu thức 3 . 3 . 3 . 3 . 3 dưới dạng lũy thừa. Hãy chỉ ra cơ số và số mũ của lũy thừa đó.
b) Tính 112.
Giải
a) 3 . 3 . 3 . 3 . 3 = 35, cơ số là 3, số mũ là 5;
b) 112 = 11.11 = 121;
Luyện tập 1
Hoàn thành bảng bình phương của các số tự nhiên từ 1 đến 10.
| a | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| a2 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
Vận dụng
(1) Tính số hạt thóc có trong ô thứ 7 của bàn cờ nói trong bài toán mở đầu.
(2) Hãy viết mỗi số tự nhiên sau thành tổng giá trị các chữ số của nó bằng cách dùng các lũy thừa của 10 theo mẫu:
4 257 = 4 . 103 + 2. 102 + 5 . 10 + 7.
a) 23 917;
b) 203 184.
Người ta đã tính được rằng tổng số thóc cần rải trên bàn cờ là 246 – 1 hạt thóc và toàn bộ khối lượng thóc này nặng tới 369 tỉ tấn. Một con số khổng lồ!
| Ta có: 100 = 102 1 000 = 103 10 000 = 104 ... |
2. NHÂN VÀ CHIA HAI LŨY THỪA CÙNG CƠ SỐ
Nhân hai lũy thừa cùng cơ số
HĐ2 a) Viết kết quả phép nhân sau dưới dạng một lũy thừa của 7:
72 . 73 = (7 . 7) . (7 . 7 . 7) = ?
b) Nêu nhận xét về mối liên hệ giữa các số mũ của 7 trong hai thừa số và trong tích tìm được ở câu a).
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và công các số mũ:
am . an = am + n.
Ví dụ 2
56 . 53 = 56 + 3 = 59 ;
105 . 104 . 102 = 105 + 4 +2 = 1011.
Luyện tập 2
Viết kết quả phép tính dưới dạng một lũy thừa:
a) 53 . 57
b) 24 . 25 . 29
c) 102 . 104 . 106 . 108
Chia hai lũy thừa cùng cơ số
HĐ3 a) Giải thích vì sao có thể viết 65 = 63 . 62
b) Sử dụng câu a) để suy ra 65 : 63 = 62. Nêu nhận xét về mối liên hệ giữa các số mũ của 6 trong số bị chia, số chia và thương.
c) Viết thương của phép chia 107 : 104 dưới dạng lũy thừa của 10.
Khi chia hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và trừ các số mũ:
am : an = am - n (với a # 0, m ≥ n).
Chú ý. Người ta quy ước a0 = 1 (với a # 0).
Ví dụ 3
26 : 23 = 26 - 3 = 23;
107 : 104 = 107 - 4 = 103;
Luyện tập 3
Viết kết quả các phép tính dưới dạng một lũy thừa:
a) 76 : 74;
b) 1 091100 : 1 091100.
BÀI TẬP
1.36. Viết các tích sau dưới dạng một lũy thừa:
a) 9 . 9 . 9 . 9 . 9
b) 10 . 10 . 10 . 10
c) 5 . 5 . 5 . 25
d) a . a . a . a . a . a
1.37. Hoàn thành bảng sau vào vở:
| Lũy thừa | Cơ số | Số mũ | Giá trị của lũy thừa |
| 43 | ? | ? | ? |
| ? | 3 | 5 | ? |
| ? | 2 | ? | 128 |
1.38. Tính: a) 25 b) 33 c) 52 c) 109.
1.39. Viết các số sau thành tổng giá trị các chữ số của nó bằng cách dùng các lũy thừa của 10: 215; 902; 2 020; 883 001.
1.40. Tính 112, 1112 . Từ đó hãy dự đoán kết quả của 1 1112.
1.41. Biết 210 = 1024. Tính 29 và 211.
1.42. Tính: a) 57 . 53 b) 58 : 54
1.43. Ta có: 1 + 3 + 5 = 9 = 32.
Viết các tổng sau dưới dạng bình phương của một số tự nhiên:
a) 1 + 3 + 5 + 7;
b) 1 + 3 + 5 + 7 + 9.
1.44. Trái Đất có khối lượng khoảng 60 . 1020 tấn. Mỗi giây Mặt Trời tiêu thụ 6 . 106 tấn khí hydrogen (theo vnexpress.net). Hỏi Mặt Trời cần bao nhiêu giây để tiêu thụ một lượng khí hydrogen có khối lượng bằng khối lượng Trái Đất?
1.45. Theo các nhà khoa học, mỗi giây cơ thể con người trung bình tạo ra khoảng 25 . 105 tế bào hồng cầu (theowww.healthline.com). Hãy tính xem mỗi giờ, bao nhiêu tế bào hồng cầu được tạo ra?
EM CÓ BIẾT?
Trong âm nhạc, người ta dùng nốt nhạc để ghi các bản nhạc. Các nốt nhạc có quan hệ trường độ như sau:
1 tròn = 21 trắng = 22 đen = 23 móc đơn = 24 móc kép.
1 trắng = 21 đen = 22 móc đơn = 23 móc kép = 24 móc ba.
(Theo sự kì diệu của Toán học, Theoni Pappas, NXB Dân Trí, 2014)












































Bình Luận
Để Lại Bình Luận Của Bạn