Trang 98
| KHÁI NIỆM, THUẬT NGỮ Hình có trục đối xứng Trục đối xứng | KIẾN THỨC, KĨ NĂNG
|
Trong thiên nhiên và trong đời sống, chúng ta thường gặp rất nhiều hình ảnh đẹp.
Khuê Văn Các
Tháp Eiffel
Mặt hồ
Các hình ảnh trên đều có sự cân đối, hài hoà. Chúng ta cùng tìm hiểu điều gì đã đem lại sự cân đối, hài hoà đó.
Trang 99
1. HÌNH CÓ TRỤC ĐỐI XỨNG TRONG THỰC TẾ
HĐ1. Quan sát hình con bướm ở hình bên.
Em thấy điều gì khi hai cánh của con bướm gập lại?
HĐ2. Vẽ một đường tròn trên giấy rồi cắt theo nét vẽ ta được một hình tròn. Gấp đôi hình tròn đó theo một đường thẳng đi qua tâm (H.5.1).
Hãy nhận xét về hai nửa hình tròn sau khi gấp.
HĐ3. Gấp đôi một tờ giấy (H.5.2a), dùng kéo cắt một đường như Hình 5.2b rồi mở ra, ta được một hình. Hình đó có đặc điểm gì giống những hình trên?
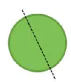
Hình 5.1
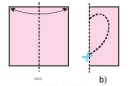
Hình 5.2
b) Các hình bên (H.5.3) đều có chung tinh chất: Có một đường thẳng d chia hình thành hai phần mà nếu “gấp” hình theo đường thẳng d thì hai phần đó "chồng khít" lên nhau.
Những hình như thế gọi là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.
a) b) c)
Hình 5.3
Luyện tập
• Những chữ cái nào dưới đây có trục đối xứng? Hãy dự đoán trục đối xứng của chúng.
ABGHEF
2. Những hình nào dưới đây có trục đối xứng?
a) 
b) 
c) 
d) 
3. Hãy tìm một ví dụ khác về hình có trục đối xứng.
Một số hình có trục đối xứng:
Trong kiến trúc
Trong thiết kế
Trang 110
2. TRỤC ĐỐI XỨNG CỦA MỘT SỐ HÌNH PHẲNG
HĐ4. Dựa vào HĐ2, em hãy cho biết trục đối xứng của hình tròn là đường thẳng nào?
HĐ5. Cắt một hình thoi bằng giấy. Hãy tìm trục đối xứng của nó bằng cách gấp giấy. Trục đối xứng của nó là đường thẳng nào? Em tìm được mấy trục đối xứng?
HĐ6.Vẽ rồi cắt một hình chữ nhật bằng giấy. Hãy tìm trục đối xứng của nó bằng cách gấp giấy. Trục đối xứng của nó là đường thằng nào? Em tìm được mấy trục đối xứng?
Nhận xét:
• Mỗi đường thẳng đi qua tâm là một trục đối xứng của hình tròn.
• Mỗi đường chéo là một trục đối xứng của hình thoi.
• Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
Mỗi hình có thể có nhiều trục đối xứng.
Thực hành 1
- Bằng cách gấp giấy, em hãy tìm một trục đối xứng của đoạn thẳng.
- Làm tương tự như HĐ6 với hình tam giác đều, hình vuông, hình lục giác đều. Em hãy chỉ ra một trục đối xứng của mỗi hình trên.
Tranh luận 1
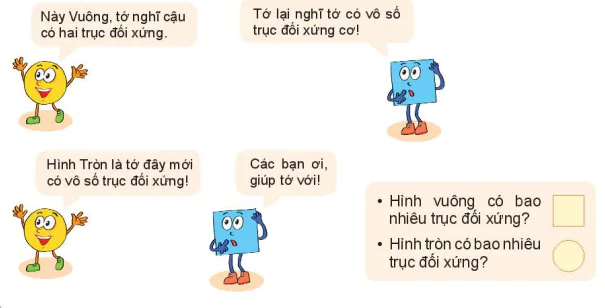
Này Vuông, tớ nghĩ cậu có hai trục đối xứng.
Tớ lại nghĩ tớ có vô số trục đối xứng cơ!
Hình Tròn là tớ đây mới có vô số trục đối xứng!
Các bạn ơi, giúp tớ với!
• Hình vuông có bao nhiêu trục đối xứng?
• Hình tròn có bao nhiêu trục đối xứng?
Trang 101
Ứng dụng tính đối xứng để cắt chữ bằng giấy
Để cắt một chữ cái có trục đối xứng, ta có thể gấp đôi tờ giấy theo trục đối xứng ấy để cắt. Khi đó ta chỉ phải cắt một nửa chữ cái và nhận được chữ cái khi mở giấy ra.
Để làm mẫu, em hãy cắt chữ A theo hướng dẫn sau (H.5.4):
1. Chuẩn bị một mảnh giấy hình chữ nhật kích thước 3 cm x 5 cm. Gấp đôi mảnh giấy như Hình 5.4b.
2. Vẽ theo Hình 5.4c rồi cắt theo nét vẽ, sau đó mở ra ta được chữ A (H.5.4d).
a)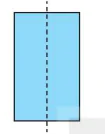 
b)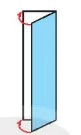 
c)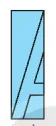 
d) 
Hình 5.4
Thực hành 2
Bằng cách tương tự, hãy cắt chữ E, Τ.
Tranh luận 2
Tớ đang gấp giấy để cắt chữ. Hãy đoán xem tớ được chữ gì sau khi mở những mảnh giấy (H.5.5) ra nhé!
a)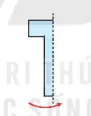 
b)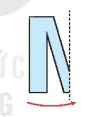 
c)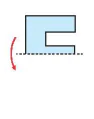 
Hình 5.5
Thử thách nhỏ
Tính đối xứng là một yếu tố tạo nên sự cân đối, hài hoà của các hình. Tuy nhiên, không phải lúc nào ta cũng có thể gấp hình để biết hình có trục đối xứng hay không. Em hãy quan sát và vẽ phác trục đối xứng của hình Tháp Chàm và ngôi sao sáu cánh dưới đây (nếu có).
Tháp Chàm
Ngôi sao sáu cảnh
Những công trình kiến trúc có tính đối xứng thì không những đẹp mà còn chắc chắn, bền vững.
Kim tự tháp Kheops (Kê-ốp) và tượng nhân sư
Trang 102
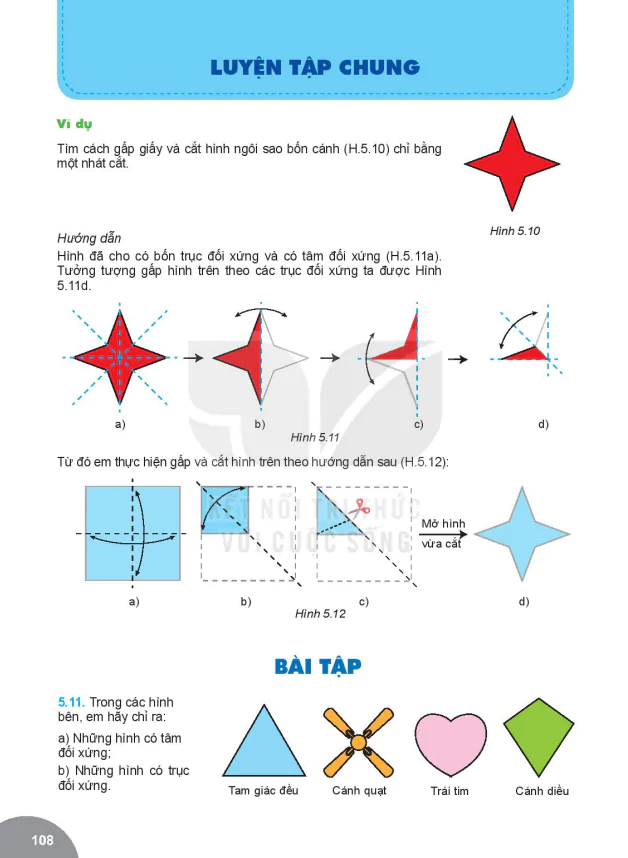
BÀI TẬP
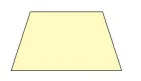
5.1. Hãy chỉ ra trục đối xứng của hình thang cân.
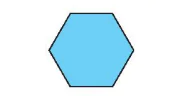
5.2. Hình lục giác đều có bao nhiêu trục đối xứng?
5.3. Trong các hình dưới đây, hình nào có trục đối xứng?
a) 
b) 
c) 
d) 
5.4. Quan sát những hình dưới đây và cho biết:
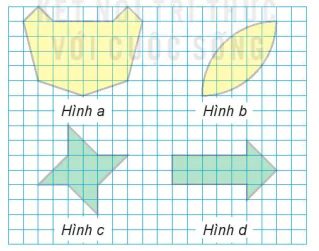
Hình a
Hình b
Hình c
Hình d
a) Hình nào không có trục đối xứng?
b) Hình nào chỉ có một trục đối xứng?
c) Hình nào có hai trục đối xứng?
Bình Luận
Để Lại Bình Luận Của Bạn