Nội Dung Chính
(Trang 21)
Kiến thức, kĩ năng
Giải một số bài toán bằng cách lập hệ phương trình bậc nhất hai ẩn.
Bài toán. Một vật có khối lượng 124 g và thể tích 15 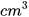
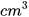 đồng nặng 8,9 g và 1
đồng nặng 8,9 g và 1 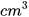 kẽm nặng 7g.
kẽm nặng 7g.
Giải bài toán bằng cách lập hệ phương trình
Xét bài toán ở Tình huống mở đầu. Gọi x là số gam đồng, y là số gam kẽm cần tính.
HĐ1 Biểu thị khối lượng của vật qua x và y.
HĐ2 Biểu thị thể tích của vật qua x và y.
HĐ3 Giải hệ gồm hai phương trình bậc nhất hai ẩn x, y nhận được ở HĐ1 và HĐ2. Từ đó trả lời câu hỏi ở Tình huống mở đầu.
Nhận xét. các bước giải một bài toán bằng cách lập hệ phương trình:
Bước 1. Lập hệ phương trình:
– Chọn ẩn số (thường chọn hai ẩn số) và đặt điều kiện thích hợp cho các ẩn số;
– Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
– Lập hệ phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2. Giải hệ phương trình.
Bước 3. Trả lời: Kiểm tra xem trong các nghiệm tìm được của hệ phương trình, nghiệm nào thoả mãn, nghiệm nào không thoả mãn điều kiện của ẩn, rồi kết luận.
Ví dụ 1
Tìm hai số tự nhiên có tổng bằng 1006, biết rằng nếu lấy số lớn chia cho số nhỏ thì được thương là 2 và số dư là 124.
Giải
- Gọi hai số cần tìm là x và y, trong đó x < y. Số dư trong phép chia y cho x là 124 nên x> 124. Vậy điều kiện của hai ẩn là x, y ∈ N và 124 < x < y.
Tổng hai số bằng 1006 nên ta có phương trình x + y = 1006.
Khi chia y cho x ta được thương là 2, dư 124 nên ta có phương trình y = 2x + 124.
Do đó, ta có hệ phương trình 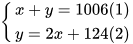
(Trang 22)
- Giải hệ phương trình:
Từ (2) thế y=2x+124 vào (1), ta được 3x+124=1006 hay 3x=882, suy ra x=294.
Từ đó ta được y=2.294+124=712
- Các giá trị x=294 và y=712 thỏa mãn các điều kiện của ẩn.
Vậy hai số cần tìm là 294 và 712
Luyện tập 1
Một chiếc xe khách đi từ Thành phố Hồ Chí Minh đến Cần Thơ, quãng đường dài 170 km. Sau khi xe khách xuất phát 1 giờ 40 phút, một chiếc xe tải bắt đầu đi từ Cần Thơ về Thành phố Hồ Chí Minh và gặp xe khách sau đó 40 phút. Tính vận tốc của mỗi xe, biết rằng mỗi giờ xe khách đi nhanh hơn xe tải 15 km.
Hướng dẫn. Gọi x (km/h) là vận tốc của xe tải và y (km/h) là vận tốc xe khách (x, y>0). Chú ý rằng hai xe (đi ngược chiều) gặp nhau khi tổng quãng đường hai xe đã đi bång 170 km.
Ví dụ 2
Hai đội công nhân cùng làm một đoạn đường trong 24 ngày thì xong. Mỗi ngày, đội I làm được nhiều gấp rưỡi đội II. Hỏi nếu làm một mình thì mỗi đội làm xong đoạn đường đó trong bao lâu? (Giả sử năng suất của mỗi đội là không đổi).
Giải
- Gọi x là số ngày để đội I hoàn thành công việc nếu làm riêng một mình; y là số ngày để đội II hoàn thành công việc nếu làm riêng một mình. Điều kiện: x > 0 và y > 0.
Mỗi ngày đội I là được 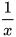 (công việc) và đôi II làm được
(công việc) và đôi II làm được 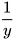
Mỗi ngày đội I làm được nhiều gấp rưỡi đội II nên ta có phương trình 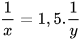
hay 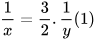
Hai đội làm chung trong 24 ngày thì xong công việc nên mỗi ngày, hai đội làm chung thì được 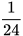 (công việc). Ta có phương trình
(công việc). Ta có phương trình
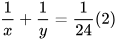
Từ (1) và (2), ta có hệ phương trình (I) 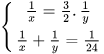
- Nếu đặt u=
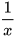 và v=
và v=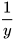 thì ta có hệ phương trình bậc nhất hai ẩn mới là u và v.
thì ta có hệ phương trình bậc nhất hai ẩn mới là u và v.
(II) 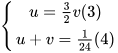
(Trang 23)
Giải hệ (II): Thế 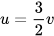 vào phương trình (4), ta được
vào phương trình (4), ta được 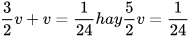
suy ra 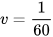 . Do đó
. Do đó 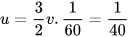 .
.
Từ đó, ta có:
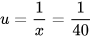 suy ra x=40;
suy ra x=40; 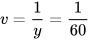 suy ra y=60.
suy ra y=60.
- Các giá trị tìmđược của x và y thỏa mãn điều kiện của ẩn.
Trả lời: Nếu làm một mình thì đội I làm xong đoạn đường đó trong 40 ngày, còn đội II làm xong trong 60 ngày.
Luyện tập 2
Nếu hai vòi nước cùng chảy vào một bể không có nước thì bể sẽ đầy trong 1 giờ 20 phút. Nếu mở riêng vòi thứ nhất trong 10 phút và vòi thứ hai trong 12 phút thì chỉ được 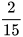
BÀI TẬP
1.15. Tìm số tự nhiên N có hai chữ số, biết rằng tổng của hai chữ số đó bằng 12, và nếu viết hai chữ số đó theo thứ tự ngược lại thì được một số lớn hơn N là 36 đơn vị.
1.16. Điểm số trung bình của một vận động viên bắn súng sau 100 lần bắn là 8,69 điểm. Kết quả cụ thể được ghi trong bảng sau, trong đó có hai ô bị mờ không đọc được (đánh dấu "?"):
| Điểm số của mỗi lần bắn | 10 | 9 | 8 | 7 | 6 |
| Số lần bắn | 25 | 42 | ? | 15 | ? |
Em hãy tìm lại các số bị mờ trong hai ô đó.
1.17. Năm ngoái, hai đơn vị sản xuất nông nghiệp thu hoạch được 3 600 tấn thóc. Năm nay, hai đơn vị thu hoạch được 4 095 tấn thóc. Hỏi năm nay, mỗi đơn vị thu hoạch được bao nhiêu tấn thóc, biết rằng năm nay, đơn vị thứ nhất làm vượt mức 15%, đơn vị thứ hai làm vượt mức 12% so với năm ngoái?
Hãy dùng máy tính cầm tay để kiểm tra lại kết quả thu được.
1.18. Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thứ nhất làm trong 3 giờ và người thứ hai làm trong 6 giờ thì chỉ hoàn thành được 25% công việc. Hỏi nếu làm riêng thì mỗi người hoàn thành công việc trong bao lâu?
(Trang 24)
BÀI TẬP CUỐI CHƯƠNG I
A. TRẮC NGHIỆM
1.19. Cặp số nào sau đây là nghiệm của hệ phương trình 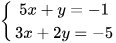 ?
?
a. (-1;1) b.(-3;2) c. (2;-3) d. (5;5)
1.20. Trên mặt phẳng tọa độ Oxy, cho các điểm A(1;2), B(5;6), C(2;3), D(-1;-1).
Đường thẳng 4x-3y=-1 đi qua hai điểm nào trong các điểm đã cho?
A. A và B; b. B và C; c. C và D d. D và A
1.21. Hệ phương trình 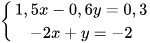
A. Có nghiệm là (0;-0,5) B. Có nghiệm là (1;0)
C. Có nghiệm là (-3;-8) D. Vô nghiệm
1.22. Hệ phương trình 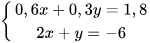
A. Có một nghiệm A. Vô nghiệm
A. Có vô số nghiệm A. Có hai nghiệm
B. TỰ LUẬN
1.23. Giải các hệ phương trình
a) 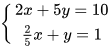 b)
b) 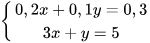
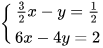
1.24. Giải các hệ phương trình
a) 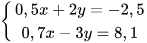 b)
b) 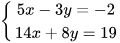 c)
c) 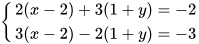
(Trang 25)
1.25. Tìm số tự nhiên N có hai chữ số, biết rằng nếu viết thêm chữ số 3 vào giữa hai chữ số của số N thì được một số lớn hơn số 2N là 585 đơn vị, và nếu viết hai chữ số của số N theo thứ tự ngược lại thì được một số nhỏ hơn số N là 18 đơn vị.
1.26. Trên cánh đồng có diện tích 160 ha của một đơn vị sản xuất, người ta dành 60 ha để cấy thí điểm giống lúa mới, còn lại vẫn cấy giống lúa cũ. Khi thu hoạch, đầu tiên người ta gặt 8 ha giống lúa cũ và 7 ha giống lúa mới để đối chứng. Kết quả là 7 ha giống lúa mới cho thu hoạch nhiều hơn 8 ha giống lúa cũ là 2 tấn thóc. Biết rằng tổng số thóc (cả hai giống) thu hoạch cả vụ trên 160 ha là 860 tấn. Hỏi năng suất của mỗi giống lúa trên 1 ha là bao nhiêu tấn thóc?
1.27. Hai vật chuyển động đều trên một đường tròn đường kính 20 cm, xuất phát cùng một lúc, từ cùng một điểm. Nếu chuyển động ngược chiều thì cứ sau 4 giây chúng lại gặp nhau. Nếu chuyển động cùng chiều thì cứ 20 giây chúng lại gặp nhau. Tính vận tốc (cm/s) của mỗi vật.
1.28. Một người mua hai loại hàng và phải trả tổng cộng là 21,7 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 21,8 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?








































Bình Luận
Để Lại Bình Luận Của Bạn