Nội Dung Chính
(Trang 108)
Ví dụ 1
Cho hai đường tròn (O; R) và (O'; R') cắt nhau tại A và B. Gọi M là điểm đối xứng với A qua O, N là điểm đối xứng với A qua O'.
a) Chứng minh rằng M ∈ (O), N ∈ (O') và ba điểm M, B, N thẳng hàng.
b) Chứng minh rằng đường thẳng MN tiếp xúc với đường tròn đường kính AB.
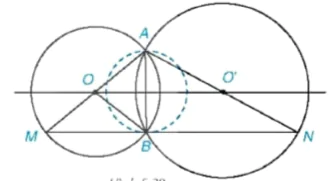
Hình 5.38
Giải (H.5.38, học sinh tự ghi giả thiết, kết luận)
a) Do tính đối xứng của (C) nên từ A ∈ (O) suy ra M ∈ (O) (vì M đối xứng với A qua O).
Tam giác ABM có BO là đường trung tuyến và 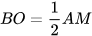 ( bán kính bằng nửa đường kính) nên là tam giác vuông tại B. Vậy
( bán kính bằng nửa đường kính) nên là tam giác vuông tại B. Vậy 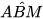 =90°.
=90°.
Tương tự, ta cũng có N ∈ (O') và 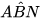 =90°. Từ hai kết quả trên suy ra
=90°. Từ hai kết quả trên suy ra
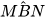 =
=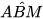
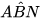 =90°+90°=180°.
=90°+90°=180°. Điều đó chứng tỏ ba điểm M, B, N thẳng hàng.
b) Kết quả câu a còn cho thấy MN ⊥ AB, tức là MN vuông góc với bán kính của đường tròn đường kính AB tại B. Do đó, MN là tiếp tuyến của đường tròn đường kính AB.
Ví dụ 2
Cho hai đường tròn ngoài nhau (O; R) và (O'; R') với giả thiết R > R'. Một đường thẳng d tiếp xúc với (O; R) tại A và tiếp xúc với (O'; R') tại B sao cho O và O' nằm cùng phía đối với d. Giả sử d cắt đường thẳng OO' tại điểm P (Hình 5.39).
a) Chứng minh rằng 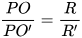 ;
;
b) Gọi A' là điểm đối xứng với A qua OO'. Chứng minh rằng đường thẳng PA' tiếp xúc với (O) và với (O').
(Trang 109)
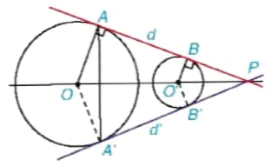
Hình 5.39)
Giải (H.5.39, học sinh tự ghi giả thiết, kết luận)
a) Do d tiếp xúc với (O) tại A, tiếp xúc với (O') tại B nên OA ⊥ d và O'B ⊥ d. Do đó, trong tam giác POA ta có O'B // OA, suy ra △POA  △PO'B. Từ đó, ta có
△PO'B. Từ đó, ta có 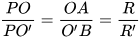
b) Do A' đối xứng với A qua OO' và A ∈ (O) nên A' ∈ (O) và OO' ⊥ AA', tức là OP ⊥ AA'.
Tam giác OAA' là tam giác cân (do OA = OA') có OP ⊥ AA' nên OP là tia phân giác của góc AOA', suy ra 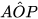 =
= 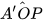
Hai tam giác AOP và A'OP có: OA = OA' (bán kính đường tròn (O)); OP chung và 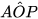 =
= 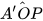 .
.
Vậy △AOP = △A'OP (c.g.c), suy ra 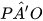
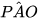 mà
mà 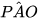 = 90° (do PA tiếp xúc với (O)) nên
= 90° (do PA tiếp xúc với (O)) nên 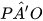 =90°.
=90°. Vậy PA' vuông góc với bán kính OA' của (O) tại A'. Điều đó chứng tỏ PA' tiếp xúc với (O) tai A'.
Đối với đường tròn (O'), gọi B' là chân đường vuông góc hạ từ O' xuống PA'. Để khẳng định rằng PA' cũng tiếp xúc với (O') tại B', ta chỉ cần chứng minh B' ∈ (O').
Thật vậy, O'B và OA' cùng vuông góc với PA' nên O'B' II OA', suy ra △POA'  △PO'B'.
△PO'B'.
Do đó
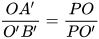
Mà theo câu a ta có  nên
nên 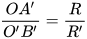 hay
hay 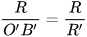 .
.
Điều này chứng tỏ O'B'=R', nghĩa là B ∈ (O')
Vậy PA' tiếp xúc với (O) tại A' và tiếp xúc với (O) tại B'.
BÀI TẬP
5.28. Cho hai đường thẳng a và b song song với nhau, điểm O nằm trong phần mặt phỏng ở giữa hai đường thẳng đó. Biết rằng khoảng cách từ O đến a và b lần lượt bằng 2 cm và 3 cm.
a) Hỏi bán kính R của đường tròn (O; R) phải thoả mãn điều kiện gì để (O; R) cắt cả hai đường thẳng a và b?
b) Biết rằng đường tròn (O; R) tiếp xúc với đường thẳng a. Hãy xác định vị trí tương đối của đường tròn (O; R) và đường thẳng b.
(Trang 110)
5.29. Khi chuyển động, giả sử đầu mũi kim dài của một chiếc đồng hồ vạch nên một đường tròn, kí hiệu là (T1), trong khi đầu mũi kim ngắn vạch nên một đường tròn khác, kí hiệu là (T2).

a) Hai đường tròn (T1) và (T2) có vị trí tương đối như thế nào?
b) Giả sử bán kính của (T1) và (T2) lần lượt là 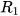
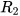 . Người ta vẽ trên mặt đồng hồ một hoạ tiết hình tròn có tâm nằm cách điểm trục kim đồng hồ một khoảng bằng
. Người ta vẽ trên mặt đồng hồ một hoạ tiết hình tròn có tâm nằm cách điểm trục kim đồng hồ một khoảng bằng 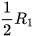 và có bán kính bằng
và có bán kính bằng 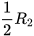 .
. Hãy cho biết vị trí tương đối của đường tròn (T3) đối với mối đường tròn (T1) và (T2). Vẽ ba đường tròn đó nếu 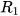 = 3 cm và
= 3 cm và 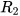
5.30. Cho đường tròn (O) đường kính AB, tiếp tuyến xx' tại A và tiếp tuyến yy' tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (P khác A và B) cắt xx' tại M và cắt yy' tại N.
a) Chứng minh rằng MN = MA + NB.
b) Đường thẳng đi qua O và vuông góc với AB cắt NM tại Q. Chứng minh rằng Q là trung điểm của đoạn MN.
c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN
5.31. Cho hai đường tròn (O) và (O') tiếp xúc ngoài với nhau tại A và cùng tiếp xúc với đường thẳng d tại B và C (khác A), trong đó B ∈ (O) và C ∈ (O'). Tiếp tuyến của (O) tại A cắt BC tại M. Chứng minh rằng:
a) Đường thẳng MA tiếp xúc với (O');
b) Điểm M là trung điểm của đoạn thẳng BC từ đó suy ra ABC là tam giác vuông.
EM CÓ BIẾT ? (Đọc thêm)
Vẽ chắp nối trơn
Trong những bản tin dự báo thời tiết trên truyền hình, các em có thể bắt gặp hình biểu tượng của đám mây như Hình 5.40.a. Quan sát đường viên của hình này, các em thấy có gì đáng chú ý?
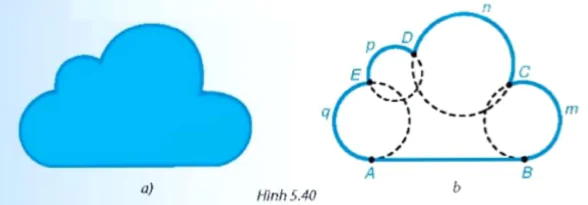
Hình 5.40
– Thứ nhất, đường viên gồm một đoạn thẳng và 4 cung tròn được chắp nối với nhau như Hình 5.40.b.
– Thứ hai, trên Hình 5.40.b, ta thấy đường viền bị "gãy" tại những điểm C, D và E (đó là những điểm chắp nối giữa hai cung tròn). Trong khi đó tại điểm chắp nối giữa đoạn thẳng AB và cung tròn AqE, đường viền không bị “gãy”. Ta nói rằng đoạn thẳng AB được chắp nối trơn với cung AqE (tại điểm A). Tương tự, cung BMC cũng được chắp nối trơn với đoạn AB (tại điểm B).
(Trang 111)
Chắp nối trơn có nhiều ứng dụng trong thực tế đời sống. Chẳng hạn, tàu hỏa phải chạy trên đường ray thẳng hoặc đường thẳng chắp nối trơn với đoạn đường cong (H.5.41).

Hình 5.41
Vậy muốn có chắp nối trơn ta làm làm thế nào? Trước hết, ta tìm hiểu về vẽ chắp nối trơn. Cách vẽ chắp nối trơn được suy ra từ hai kết luận sau:
1) Nếu một đoạn thẳng được chắp nối trơn với một cung tròn thì đoạn thẳng đó nằm trên tiếp tuyến của đường tròn chứa cung tròn đó tại điểm chắp nối.
2) Nếu hai cung tròn được chắp nối trơn với nhau thì hai đường tròn chứa hai cung ấy tiếp xúc nhau tại điểm chắp nối.
Để hiểu thêm về về chắp nối trơn, em hãy chuẩn bị thước kẻ và compa để vẽ hình "trái xoan" (H.5.42) theo hướng dẫn sau đây:
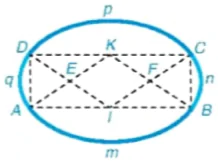
Hình 5.42
– Vẽ hình chữ nhật ABCD (kích thước tuỳ ý).
– Xác định trung điểm I của đoạn AB và trung điểm K của đoạn CD.
– Tìm giao điểm E của AK và DI; giao điểm F của BK và CI.
– Vẽ 4 cung: 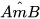 (tâm K),
(tâm K), 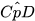
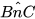 (tâm F) và
(tâm F) và 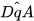 (tâm E).
(tâm E). Bốn cung tròn vừa về tạo nên hình “trái xoan". Trong hình đó, tâm của hai cung liên tiếp, chẳng hạn, tâm K của cung AmB và tâm F của cung BnC thẳng hàng với điểm chắp nối B, chứng tỏ hai đường tròn (K) và (F) tiếp xúc nhau tại điểm B. Điều đó cho phép hai cung này chắp nối trơn với nhau tại B.
Em hãy tìm hiểu điều tương tự đối với các cặp cung liên tiếp còn lại để hiểu tại sao các cung tròn đã vẽ đều chắp nối trơn với nhau.
Bây giờ em hãy tự mình tìm hiểu và trao đổi với các bạn khác về cách vẽ hai hình sau đây nhé!
|
Hình “quảng trứng” |
Biểu tượng “gió” trong dự báo thời tiết |








































Bình Luận
Để Lại Bình Luận Của Bạn