Nội Dung Chính
(Trang 119)
| THUẬT NGỮ | GIẢI THÍCH |
| Bất đẳng thức | Hệ thức có dạng a>b (hay a<b, a≥b, a≤b). |
| Bất phương trình bậc nhất một ẩn | Bất phương trình dạng ax+b<0 (hoặc ax+b>0, ax+b≤0, ax+b≥0) |
| Căn bậc ba | Căn bậc ba của số thực a là số thực x sao cho 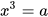 |
| Căn bậc hai | Căn bậc hai của số thực không âm a là số thực x sao cho 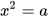 |
| Căn thức bậc hai | Biểu thức có dạng 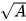 , trong đó A là một biểu thức đại số , trong đó A là một biểu thức đại số |
| Cung tròn | Phần đường tròn giới hạn bởi hai điểm nằm trên đường tròn |
| Dây cung | Đoạn thẳng nối hai điểm tùy ý của một đường tròn |
| Điều kiện xác định của phương trình | Điều kiện của ẩn để các biểu thức trong phương trình có nghĩa |
| Giải bất phương trình | Tìm nghiệm của bất phương trình đó |
| Giải tam giác vuông | Tìm tất cả các cạnh và các góc của một tam giác vuông, khi biết hai cạnh hoặc một cạnh và một góc nhọn của tam giác vuông đó. |
| Góc ở tâm | Góc có đỉnh trùng với tâm đường tròn |
| Hai đường tròn cắt nhau | Hai đường tròn có hai điểm chung |
| Hai đường tròn không giao nhau | Hai đường tròn không có điểm chung |
| Hai đường tròn tiếp xúc nhau | Hai đường tròn có đúng một điểm chung |
| Hai góc phụ nhau | Hai góc nhọn có tổng bằng 90° |
| Hệ hai phương trình bậc nhất hai ẩn | Một cặp gồm hai phương trình bậc nhất hai ẩn |
| Hình quạt tròn | Một phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai mút của cung đó. |
| Hình vành khuyên | Phần nằm giữa hai đường tròn đồng tâm |
| Nghiệm của bất phương trình | Số 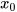 là một nghiệm của bất phương trình A(x) <B(x) nếu A( là một nghiệm của bất phương trình A(x) <B(x) nếu A(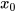 )<B( )<B(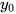 |
| Nghiệm của hệ hai phương trình bậc nhất hai ẩn | Cặp số (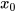 ; ;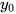 ) đồng thời là nghiệm của cả hai phương trình của hệ ) đồng thời là nghiệm của cả hai phương trình của hệ |
| Phép khai căn bậc hai | Phép toán tìm căn bậc hai số học của số không âm |
| Phương trình bậc nhất hai ẩn | Hệ thức ax+by=c, trong đó a, b, c là các số đã biết (a≠0) hoặc (b≠0) |
| Tỉ số lượng giác của góc nhọn | Bao gồm sin, côsin, tang và côtang của góc nhọn đó |
| Tiếp điểm | Điểm tiếp xúc giữa đường thẳng và đường tròn hoặc giữa hai đường tròn |
| Tiếp tuyến của đường tròn | Đường thẳng chỉ có một điểm chung với đường tròn |
| Trục căn thức ở mẫu | Phép biến đổi làm mất căn thức ở mẫu của một biểu thức. |








































Bình Luận
Để Lại Bình Luận Của Bạn