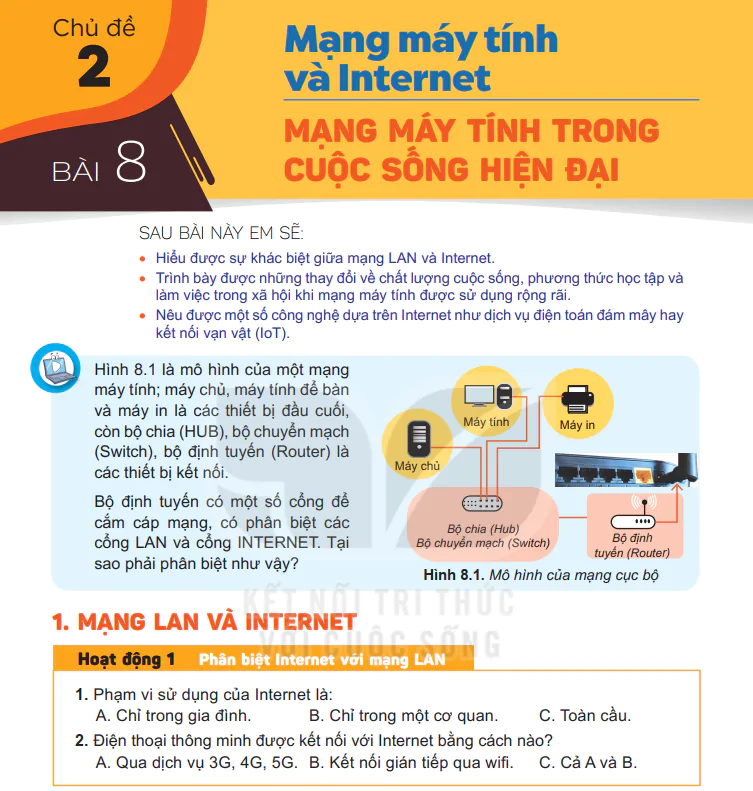
Nội Dung Chính
Trang 20
MỤC TIÊU
SAU BÀI NÀY EM SẼ:
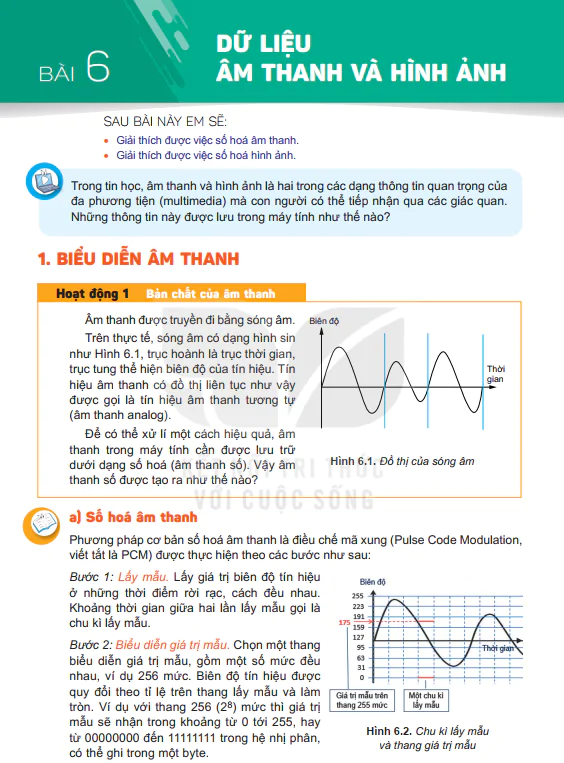
• Biết được hệ nhị phân và biểu diễn số nguyên trong máy tính.
• Giải thích được ứng dụng của hệ nhị phân trong tin học.
KHỞI ĐỘNG
Trong hệ thập phân, mỗi số có thể được phân tích thành tổng các luỹ thừa của 10 với hệ số của mỗi số hạng chính là các chữ số tương ứng của số đó. Ví dụ số 513 có thể viết thành: 5 x 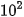
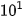 + 3 x
+ 3 x 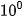
Ta cũng có thể phân tích một số thành tổng các luỹ thừa của 2, chẳng hạn 13 có thể viết thành: 1 x 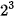 + 1 x
+ 1 x 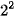 + 0 x
+ 0 x 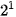
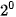 với các hệ số chỉ là 0 hay 1.
với các hệ số chỉ là 0 hay 1. Khi đó, có thể thể hiện 13 bởi 1101 được không? Em hãy cho biết việc thể hiện giả trị của một số bằng dãy bit có lợi gì.
NỘI DUNG BÀI HỌC
1. HỆ NHỊ PHÂN VÀ BIỂU DIỄN SỐ NGUYÊN
| Hoạt động 1: Biểu diễn một số dưới dạng tổng luỹ thừa của 2 Em hãy viết số 19 thành một tổng các luỹ thừa của 2. Gợi ý: Hãy lập danh sách các luỹ thừa của 2 như 16, 8, 4, 2, 1 và tách dần khỏi 19 cho đến hết. |
a) Hệ nhị phân
Số 19 có thể được biểu diễn bằng tổng 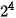 +
+ 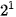 +
+ 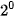 hoặc viết dưới dạng đầy đủ các luỹ thừa: 1 x
hoặc viết dưới dạng đầy đủ các luỹ thừa: 1 x 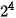
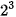 + 0 x
+ 0 x 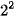 + 1 x
+ 1 x 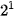 + 1 x
+ 1 x 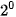
Tương tự như hệ thập phân, 2 có thể được dùng làm cơ số cho một hệ đếm gọi là hệ đếm cơ số 2 hay hệ nhị phân với các đặc điểm sau:
– Chỉ dùng hai chữ số là 0 và 1, các chữ số 0 và 1 gọi là các chữ số nhị phân.
– Mỗi số có thể biểu diễn bởi một dãy các chữ số nhị phân.
– Trong biểu diễn số nhị phân, một chữ số ở một hàng sẽ có giá trị gấp 2 lần chính chữ số đó ở hàng liền kề bên phải. Vì vậy chữ số 1 ở vị trí thứ k kể từ phải sang trái sẽ mang giá trị là 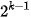
Trong hệ nhị phân, số 19 sẽ có biểu diễn là 10011. Khi cần phân biệt số được biểu diễn trong hệ đếm nào người ta viết cơ số làm chỉ số dưới như 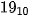 hay
hay 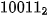 .
.
b) Đổi biểu diễn số nguyên dương từ hệ thập phân sang hệ nhị phân
Giả sử cần đổi số tự nhiên N trong hệ thập phân sang số nhị phân có dạng 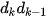 ...
...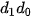 , nghĩa là cần tìm các số
, nghĩa là cần tìm các số 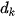
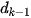 ,....,
,...., 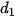 ,
, 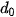 có giá trị bằng 0 hoặc 1
có giá trị bằng 0 hoặc 1sao cho
N = 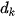 x
x 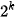
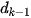 x
x 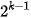 + ... +
+ ... + 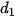 x 2 +
x 2 + 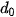
Trang 21
-1
Để tìm các số 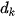
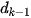 ,...,
,..., 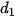 ,
, 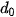 , người ta chia liên tiếp N cho 2 để tìm số dư như minh hoạ việc đổi số 19 sang số nhị phân ở Hình 4.1.
, người ta chia liên tiếp N cho 2 để tìm số dư như minh hoạ việc đổi số 19 sang số nhị phân ở Hình 4.1. 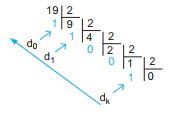
Hình 4.1. Đổi một số từ hệ thập phân sang hệ nhị phân
Viết các số dư theo chiều từ dưới lên, ta được số nhị phân cần tìm:
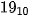
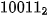 .
. Việc đổi số nhị phân có dạng 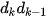 ,...
,...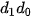 sang số thập phân thực chất chỉ là việc tính tổng
sang số thập phân thực chất chỉ là việc tính tổng 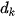 ×
× 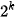
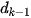 x
x 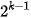 + + ... +
+ + ... + 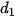 x 2 +
x 2 + 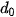 . Ví dụ:
. Ví dụ: 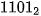
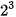 + 1 x
+ 1 x 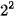 + 0 x
+ 0 x 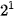 + 1 x
+ 1 x 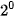 = 13.
= 13. c) Biểu diễn số nguyên trong máy tính
Có hai phương pháp để biểu diễn số trong máy tính là dấu phẩy tĩnh và dấu phẩy động, trong đó phương pháp dấu phẩy động thường được dùng khi tính toán với các số quá lớn, quá nhỏ hoặc không nguyên (có phần thập phân). Dưới đây chúng ta chỉ đề cập tới cách biểu diễn số nguyên.
Biểu diễn số nguyên không dấu chính là thể hiện của số trong hệ đếm cơ số 2. Khi được đưa vào bộ nhớ, tuỳ theo số nhỏ hay lớn mà có thể phải dùng một hay nhiều byte. Ví dụ số 19 trong hệ đếm nhị phân có biểu diễn là 10011 chỉ cần một byte với ba bit 0 bổ sung thêm bên trái cho đủ 8 bit, nhưng số 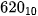
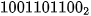 sẽ phải sử dụng 2 byte và cần bổ sung thêm 6 bit 0 vào phía trái cho đủ 16 bit.
sẽ phải sử dụng 2 byte và cần bổ sung thêm 6 bit 0 vào phía trái cho đủ 16 bit. Đối với số nguyên có dấu, có một số cách mã hoá như mã thuận (còn gọi là mã dấu – lượng), mã bù 1 (còn gọi là mã đảo) và mã bù 2. Cả ba cách mã hoá này đều dành ra một bit tận cùng bên trái để mã hoá dấu, dấu + được mã hoá bởi bit 0, dấu – được mã hoá bởi bit 1. Số dương trong cả ba cách mã hoá này đều giống nhau, sau bit dấu (bit 0) là biểu diễn nhị phân của số. Đối với số âm thì biểu diễn của ba cách mã hoá này khác nhau. Ví dụ số 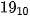 trong cả ba cách mã hoá đều có mã là 00010011. Trong khi đó số
trong cả ba cách mã hoá đều có mã là 00010011. Trong khi đó số 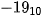 sẽ có mã thuận là 10010011, mã bù 1 là 11101100 và mã bù 2 là 11101101.
sẽ có mã thuận là 10010011, mã bù 1 là 11101100 và mã bù 2 là 11101101.
| • Hệ nhị phân chỉ dùng hai chữ số 0 và 1. Mọi số đều có thể biểu diễn được trong hệ nhị phân. Nhờ vậy, có thể biểu diễn số trong máy tính. • Biểu diễn số nguyên dương trong máy tính được thực hiện một cách tự nhiên bằng cách đổi biểu diễn số sang hệ nhị phân rồi đưa vào bộ nhớ máy tính. Đối với các số nguyên có dấu, có nhiều kiểu biểu diễn khác nhau. |
Câu hỏi
1. Em hãy đổi các số sau từ hệ thập phân sang hệ nhị phân.
a) 13.
b) 155.
c) 76.
2. Em hãy đổi các số sau từ hệ nhị phân sang hệ thập phân.
a) 110011.
b) 10011011.
c) 1001110.
Trang 22
2. CÁC PHÉP TÍNH SỐ HỌC TRONG HỆ NHỊ PHÂN
Các phép tính trong hệ nhị phân sẽ được thực hiện như thế nào?
Trong phần này, chúng ta sẽ làm quen với các phép toán cộng và nhân.
| Hoạt động 2: Phép tính trong hệ nhị phân Hãy chuyển các toán hạng của hai phép tính sau ra hệ nhị phân để chuẩn bị kiểm tra kết quả thực hiện các phép toán trong hệ nhị phân. (Ví dụ 3 + 4 = 7 sẽ được chuyển dạng thành 11 + 100 = 111). a) 26 +27=53. b) 5 x 7 = 35. |
a) Bảng cộng và nhân trong hệ nhị phân
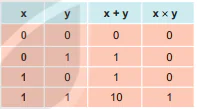
Bảng 4.1 là bảng cộng và nhân trong hệ nhị phân tương tự hệ thập phân. Lưu ý là 1+1=10.
| x | y | x + y | x × y |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 10 | 1 |
Bảng 4.1. Bảng cộng và nhân trong hệ nhị phân
b) Cộng hai số nhị phân
Phép cộng cũng được thực hiện tương tự như trong hệ thập phân, thực hiện từ phải sang trái.
Khi phép cộng hai bit có kết quả là 10 thì ghi 0 ở hàng tương ứng dưới tổng và nhớ 1 sang hàng bên trái. Có thể xảy ra trường hợp cộng hai bit 1 mà phải nhớ 1 từ hàng trước chuyển sang thì kết quả sẽ là 11, khi đó chúng ta ghi 1 ở hàng tương ứng dưới tổng và nhớ 1 sang hàng tiếp theo bên trái.
Hình 4.2 minh hoạ phép cộng hai số nhị phân 11011 và 11010.
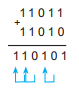
Hình 4.2. Thực hiện phép cộng
c) Nhân hai số nhị phân
Phép nhân trong hệ nhị phân cũng được thực hiện tương tự như trong hệ thập phân.
Ta sẽ nhân thừa số thứ nhất lần lượt với từng chữ số của thừa số thứ hai, theo thứ tự từ phải sang trái và đặt kết quả căn phải theo đúng vị trí chữ số của thừa số thứ hai, rồi cộng tất cả lại (Hình 4.3).
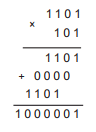
Hình 4.3. Thực hiện phép nhân
Trang 23
| • Các phép tính số học trên hệ nhị phân ũng tương tự như thực hiện trên hệ thập phân. • Do máy tính biểu diễn số trên hệ nhị phân nên máy tính cần thực hiện các phép tính số học trực tiếp trên hệ nhị phân. Vì vậy, có thể coi tính toán số học trong máy tính là ứng dụng của hệ nhị phân. |
Câu hỏi
Hãy thực hiện các phép tính sau trong hệ nhị phân:
a) 101101 + 11001.
b) 100111 x 1011.
LUYỆN TẬP
"Thực hiện tính toán trên máy tính luôn theo quy trình sau:

01: Mã hoá dữ liệu (đổi từ hệ thập phân sang hệ nhị phân)
02: Thực hiện phép tính trong hệ nhị phân
03: Giải mã kết quả (đổi kết quả từ hệ nhị phân sang hệ thập phân)
Hình 4.4. Quy tình tực hiện phốp tính trên máy tính
1. Hãy thực hiện các phép tính sau đây theo quy trình Hình 4.4.
a) 125 + 17.
b) 250 + 175.
c)76 + 112.
2. Em hãy thực hiện các phép tính sau đây theo quy trình Hình 4.4.
a) 15 × 6.
b) 11 × 9.
c) 126 × 4.
VẬN DỤNG
1. Em hãy tìm hiểu trên Intemet hoặc các tài liệu khác cách đổi phần thập phân của một số trong hệ thập phân sang hệ đếm nhị phân.
2. Em hãy tìm hiểu mã bù 2 với hai nội dung:
a) Mã bù 2 được lập như thể nào?
b) Mã bù 2 được dùng để làm gì?






































































Bình Luận
Để Lại Bình Luận Của Bạn