Trang 46
Hình 4.1 cho thấy ga An Cựu cách Hoàng cung Huế 3,01 km về hướng đông nam. Hai thông tin khoảng cách và hướng cho phép ta xác định được vị trí của ga An Cựu theo vị trí của Hoàng cung Huế.
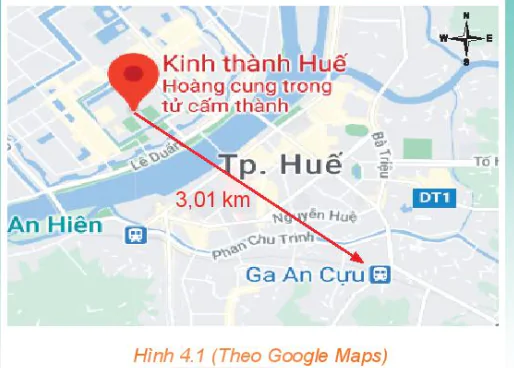
Hình 4.1 (Theo Google Maps)
Một số đại lượng như lực, vận tốc cũng được đặc trưng bởi hai yếu tố là độ lớn và hướng. Chương này xây dựng một đối tượng toán học, được gọi là vectơ, mà ta có thể dùng nó để biểu diễn các đại lượng nói trên.
Vectơ còn được sử dụng để xây dựng các khái niệm toán học, là công cụ để giải quyết nhiều bài toán và góp phần vào việc hình thành và phát triển năng lực tư duy tuyến tính cho người học.
| THUẬT NGỮ • Vectơ • Vecto-không • Độ dài của vectơ • Hai vectơ cùng phương • Hai vectơ cùng hướng • Hai vectơ bằng nhau | KIẾN THỨC, KĨ NĂNG • Nhận biết khái niệm vectơ, hai vectơ cùng phương, hai vectơ cùng hướng, hai vectơ bằng nhau, vectơ-không. • Biểu thị một số đại lượng như lực, vận tốc bằng vectơ |
Nhiệt độ và gió là hai yếu tố luôn cùng được đề cập trong các bản tin dự báo thời tiết. Tuy nhiên, nhiệt độ là đại lượng chỉ có độ lớn, còn gió có cả hướng và độ lớn. Với một đơn vị đo ta có thể dùng số để biểu diễn nhiệt độ. Đối với các đại lượng gồm hướng và độ lớn như vận tốc gió thì sao? Ta có thể dùng đối tượng toán học nào để biểu diễn chúng?

Nhiệt độ: 30°C
Gió: đông nam, 18 km/h.
Trang 47
1. KHÁI NIỆM VECTƠ
HĐ1. Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km về hướng nam thì tới đảo B (H.4.2). Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng nào và quãng đường phải đi dài bao nhiêu kilômét?
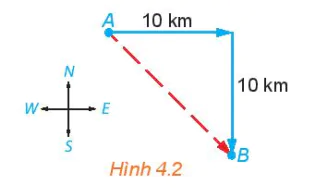
Hình 4.2
Ta có thể gắn cho quãng đường thẳng từ đảo A tới đảo B đồng thời hai yếu tố, đó là độ dài và hướng (hướng đi thẳng từ đảo A tới đảo B). Từ thực tế này, ta đi tới khái niệm toán học sau:
| • Vectơ là một đoạn thẳng có hướng, nghĩa là, trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu, điểm cuối. • Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. |
Chú ý
• Vectơ có điểm đầu A và điểm cuối B được kí hiệu là 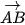 , đọc là vectơ AB (H.4.3).
, đọc là vectơ AB (H.4.3).
• Để vẽ một vectơ, ta vẽ đoạn thẳng nối điểm đầu và điểm cuối của nó, rồi đánh dấu mũi tên ở điểm cuối (H.4.3).
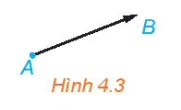
Hình 4.3
• Vectơ còn được kí hiệu là 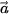
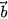 ,
, 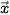 ,
, 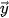 ,... (H.4.4).
,... (H.4.4). 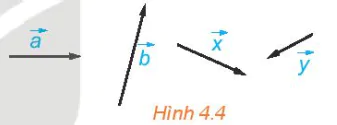
Hình 4.4
• Độ dài của vectơ 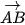
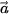 tương ứng được kí hiệu là
tương ứng được kí hiệu là 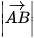 ,
, 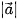 .
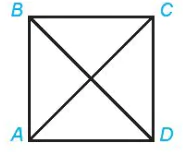
. Ví dụ 1. Cho hình vuông ABCD với cạnh có độ dài bằng 1. Tính độ dài các vectơ 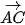 ,
, 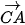
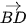 .
. 
Giải
Vì cạnh của hình vuông ABCD có độ dài bằng 1 nên các đường chéo của hình vuông này có độ dài bằng 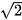 .
.
Vậy 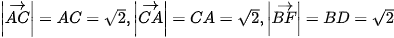
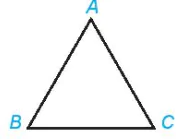
Luyện tập 1. Cho tam giác đều ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC.
2. HAI VECTƠ CÙNG PHƯƠNG, CŨNG HƯỚNG, BĂNG NHAU
HĐ2. Quan sát các làn đường trong Hình 4.5 và cho biết những nhận xét nào sau đây là đúng.
a) Các làn đường song song với nhau.
b) Các xe chạy theo cùng một hướng.
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau.
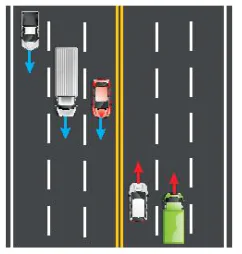
Hình 4.5
Trang 48
| • Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó. • Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau. |
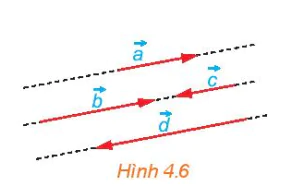
Hình 4.6
Trong Hình 4.7, mỗi cặp vectơ trong các vectơ 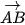 ,
, 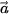 ,
, 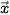
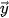 ,
, 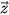 đều cùng phương, nhưng vectơ
đều cùng phương, nhưng vectơ 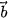 không cùng phương với mỗi vectơ trên.
không cùng phương với mỗi vectơ trên. 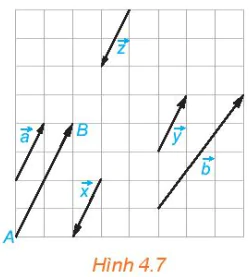
Hình 4.7
HD3. Xét các vectơ cùng phương trong Hình 4.7. Hai vectơ 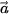
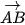 được gọi là cùng hướng, còn hai vectơ
được gọi là cùng hướng, còn hai vectơ 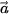 và
và 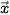 được gọi là ngược hướng. Hãy chỉ ra các vectơ cùng hướng với vectơ
được gọi là ngược hướng. Hãy chỉ ra các vectơ cùng hướng với vectơ 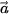 và các vectơ ngược hướng với vecto
và các vectơ ngược hướng với vecto 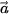
| Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng. |
Hai vectơ 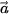 và và 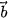 được gọi là bằng nhau, kí hiệu được gọi là bằng nhau, kí hiệu 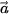 = =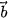 , nếu chúng có cùng độ dài và cùng hướng. , nếu chúng có cùng độ dài và cùng hướng. |
Chỉ khi hai vectơ cùng phương, ta mới nói tới chúng cùng hướng hay ngược hướng.

Chú ý
• Ta cũng xét các vectơ có điểm đầu và điểm cuối trùng nhau (chẳng hạn 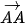 ,
, 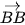 ,
, 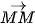 ), gọi là các vectơ-không.
), gọi là các vectơ-không.
• Ta quy ước vectơ-không có độ dài bằng 0, cùng hướng (do đó cùng phương) với mọi vectơ.
• Các vectơ-không có cùng độ dài và cùng hướng nên bằng nhau và được kí hiệu chung là 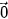 .
.
• Với mỗi điểm O và vectơ 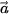
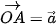 . (H.4.8)
. (H.4.8) 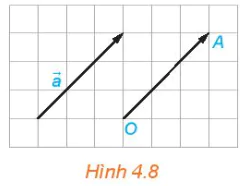
Ví dụ 2. Cho hình chữ nhật ABCD. Hãy chỉ ra mối quan hệ về độ dài, phương, hướng giữa các cặp vectơ: 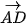 và
và 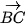 ,
, 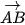
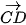 ,
, 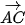 và
và 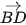 . Những cặp vectơ nào trong các cặp vectơ trên là bằng nhau?
. Những cặp vectơ nào trong các cặp vectơ trên là bằng nhau? Giải (H.4.9)
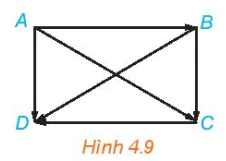
Hình 4.9
• Hai vectơ 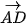
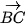 có cùng độ dài và cùng hướng. Do đó, hai vectơ
có cùng độ dài và cùng hướng. Do đó, hai vectơ 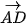 và
và 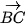 bằng nhau.
bằng nhau. • Hai vectơ 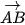 và
và 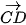
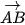 và
và 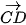 không bằng nhau.
không bằng nhau. • Hai vectơ 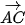 và
và 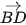 có cùng độ dài nhưng không cùng phương nên không cùng hướng. Do đó, hai vectơ
có cùng độ dài nhưng không cùng phương nên không cùng hướng. Do đó, hai vectơ 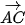
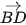 không bằng nhau.
không bằng nhau. Vậy trong các cặp vectơ đang xét, chỉ có cặp vectơ 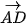 và
và 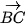 là bằng nhau (
là bằng nhau (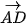 =
= 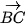
Trang 49
Luyện tập 2. Cho hình thang cân ABCD với hai đáy AB, CD, AB < CD (H.4.10). Hãy chỉ ra mối quan hệ về độ dài, phương, hướng giữa các cặp vectơ 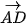 và
và 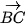 ,
, 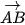 và
và 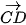 ,
, 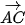
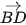 . Có cặp vectơ nào trong các cặp vectơ trên bằng nhau hay không?
. Có cặp vectơ nào trong các cặp vectơ trên bằng nhau hay không? 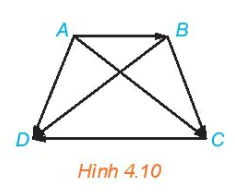
Hình 4.10
Ví dụ 3. Chứng minh rằng ba điểm A, B, C thẳng hàng khi và chỉ khi hai vectơ 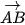 ,
, 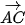 cùng phương.
cùng phương.
Giải
• Giả sử ba điểm A, B, C thẳng hàng. Khi đó, chúng cùng thuộc một đường thẳng d. Vậy hai vectơ 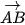
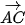 có cùng giá là d. Suy ra chúng cùng phương.
có cùng giá là d. Suy ra chúng cùng phương.• Giả sử hai vectơ
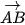 ,
, 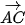 cùng phương. Khi đó, chúng có cùng giá hoặc có hai giá song song với nhau. Mặt khác, giá của các vectơ trên đều đi qua A nên chúng trùng nhau. Vậy A, B, C thẳng hàng.
cùng phương. Khi đó, chúng có cùng giá hoặc có hai giá song song với nhau. Mặt khác, giá của các vectơ trên đều đi qua A nên chúng trùng nhau. Vậy A, B, C thẳng hàng.Ta có thể dùng ngôn ngữ vectơ để biểu thị một số quan hệ hình học.

Nhận xét. Ba điểm A, B, C thẳng hàng khi và chỉ khi 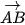
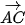 cùng phương.
cùng phương. Luyện tập 3. Trong các điều kiện dưới đây, chọn điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B.
a) 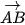 và
và 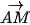 ngược hướng. b)
ngược hướng. b) 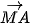 và
và 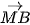
c) 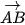 và
và 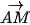 cùng hướng. d)
cùng hướng. d) 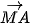 và
và 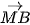 ngược hướng.
ngược hướng.
Chú ý. Ta có thể dùng vectơ để biểu diễn các đại lượng như lực, vận tốc, gia tốc. Hướng của vectơ chỉ hưởng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.
Ví dụ 4. Một vật A được thả chim hoàn toàn dưới đáy một cốc chất lỏng. Biết rằng trong ba cách biểu diễn lực đẩy Archimedes (Ác-si-mét) 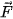
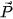 tác động lên vật A ở Hình 4.11, có một cách biểu diễn đúng.
tác động lên vật A ở Hình 4.11, có một cách biểu diễn đúng. 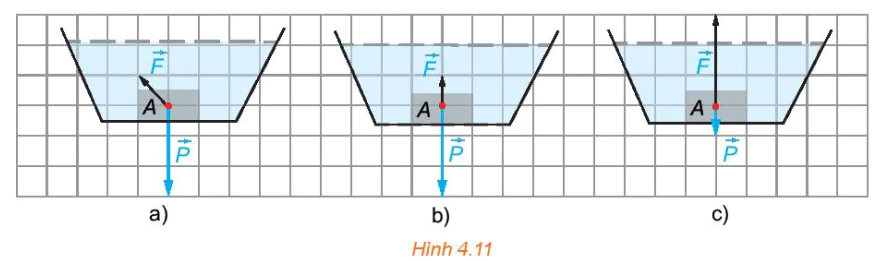
a) b) c)
Hình 4.11
Hãy chỉ ra mối quan hệ giữa trọng lượng riêng của vật A và trọng lượng riêng của chất lỏng trong cốc.
Trang 50
Giải
Lực đẩy Archimedes và trọng lực đều tác động lên vật A theo phương thẳng đứng, hai lực này cùng phương nhưng ngược hướng. Do đó, Hình 4.11a không đúng. Vật A chìm xuống đáy nên trọng lực P (có hướng từ trên xuống) lớn hơn lực đẩy Archimedes F (có hướng từ dưới lên). Do vậy, Hình 4.11c không đúng.
Vậy hình biểu diễn đúng là Hình 4.11b. Theo đó, vectơ biểu diễn lực P có độ dài gấp 3 lần độ dài của vectơ biểu diễn lực F.
Độ lớn của trọng lực và lực đẩy Archimedes tác động lên A là: 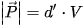 , trong đó V (
, trong đó V (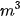 ) là thể tích của vật A và d', d (N/
) là thể tích của vật A và d', d (N/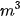
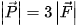 (theo H.4.11b) nên d' = 3d. Vậy trọng lượng riêng của vật A gấp 3 lần trọng lượng riêng của chất lỏng trong cốc.
(theo H.4.11b) nên d' = 3d. Vậy trọng lượng riêng của vật A gấp 3 lần trọng lượng riêng của chất lỏng trong cốc. Vận dụng. Hai ca nô A và B chạy trên sông với các vận tốc riêng có cùng độ lớn là 15 km/h. Tuy vậy, ca nô A chạy xuôi dòng còn ca nô B chạy ngược dòng. Vận tốc của dòng nước trên sông là 3 km/h.
a) Hãy thể hiện trên hình vẽ, vectơ vận tốc 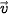 của dòng nước và các vectơ vận tốc thực tế
của dòng nước và các vectơ vận tốc thực tế 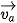 ,
, 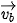 của các ca nô A, B.
của các ca nô A, B.
b) Trong các vectơ 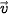
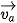 ,
, 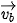 , những cặp vectơ nào cùng phương và những cặp vectơ nào ngược hướng?
, những cặp vectơ nào cùng phương và những cặp vectơ nào ngược hướng? BÀI TẬP
4.1. Cho ba vectơ 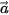 ,
, 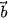 ,
, 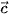
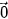 . Những khẳng định nào sau đây là đúng?
. Những khẳng định nào sau đây là đúng? a) 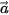 ,
, 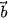 ,
, 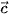 đều cùng hướng với 0;
đều cùng hướng với 0;
b) Nếu 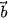
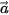 thì
thì 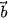 ngược hướng với
ngược hướng với 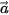 ;
; c) Nếu 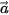 và
và 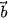
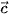 thì
thì 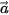 và
và 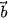 cùng phương;
cùng phương; d) Nếu 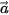 và
và 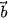
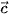 thì
thì 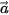 và
và 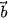 cùng hướng.
cùng hướng. 4.2. Trong Hình 4.12, hãy chỉ ra các vectơ cùng phương, các cặp vectơ ngược hướng và các cặp vectơ bằng nhau.
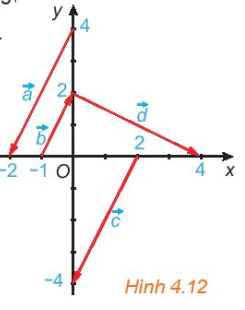
Hình 4.12
4.3. Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi 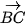
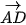 .
.
4.4. Cho hình vuông ABCD có hai đường chéo cắt nhau tại 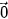 . Hãy chỉ ra tập hợp S gồm tất cả các vectơ khác có điểm đầu và điểm cuối thuộc tập hợp {A; B; C, D; O}. Hãy chia tập S thành các nhóm sao cho hai vectơ thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
. Hãy chỉ ra tập hợp S gồm tất cả các vectơ khác có điểm đầu và điểm cuối thuộc tập hợp {A; B; C, D; O}. Hãy chia tập S thành các nhóm sao cho hai vectơ thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
4.5. Trên mặt phẳng toạ độ Oxy, hãy vẽ các vectơ 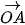 ,
, 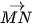 với A(1; 2), M(0; −1), N(3; 5).
với A(1; 2), M(0; −1), N(3; 5).
a) Chỉ ra mối quan hệ giữa hai vectơ trên.
b) Một vật thể khởi hành từ M và chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn bởi vectơ 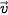
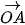 . Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu vật sẽ tới N?
. Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu vật sẽ tới N?







































































Bình Luận
Để Lại Bình Luận Của Bạn