Nội Dung Chính
Trang 71
A - TRẮC NGHIỆM
4.27. Trong mặt phẳng toạ độ, cặp vectơ nào sau đây có cùng phương?
A. 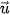
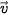 =
= 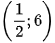 . B.
. B.  = (
= (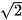 ;6) và
;6) và 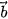
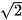 ).
). C. 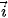 = (0;1) và
= (0;1) và 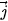 = (1;0). D.
= (1;0). D. 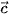 = (1;3) và
= (1;3) và 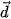
4.28. Trong mặt phẳng toạ độ, cặp vectơ nào sau đây vuông góc với nhau?
A. 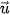 = (2;3) và
= (2;3) và 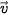 = (4;6). B.
= (4;6). B.  = (1;−1) và b = (-1;1).
= (1;−1) và b = (-1;1).
C. 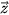 = (a;b) và
= (a;b) và 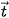
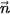 =(1;1) và
=(1;1) và 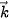 =(2;0).
=(2;0). 4.29. Trong mặt phẳng toạ độ, vectơ nào sau đây có độ dài bằng 1?
A.  = (1,1). B.
= (1,1). B. 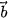 = (1;-1).
= (1;-1).
C. 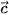
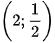 . D.
. D. 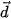 =
= 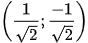 .
.4.30. Góc giữa vectơ
 = (1;−1) và vectơ
= (1;−1) và vectơ 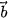
A. 90°. B. 0° C. 135° D. 45°.
4.31. Khẳng định nào sau đây là đúng?
A. ( ⋅
⋅ 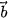 )
)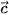 =
=  (
(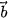
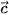 ). B.
). B. 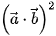 =
= 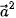 ⋅
⋅ 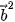 .
. C. 
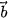 = |
= | | ⋅ |
| ⋅ |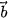 |sin(
|sin( ,
,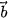
 (
(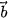 -
- 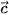 ) =
) =  ⋅
⋅ 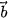
 ⋅
⋅ 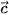 .
. 4.32. Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?
A. (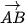 ,
,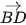 ) = 45°. B. (
) = 45°. B. (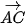
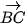 ) = 45° và
) = 45° và 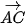 ⋅
⋅ 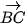 =
= 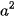 .
. C. 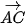
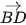 =
= 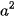
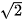 . D.
. D. 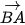 ⋅
⋅ 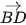
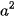 .
. B - TỰ LUẬN
4.33. Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3MC.
a) Tìm mối liên hệ giữa hai vectơ 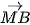 và
và 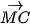 .
.
b) Biểu thị vecto 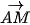 theo hai vectơ
theo hai vectơ 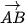
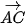 .
. Trang 72
4.34. Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:
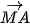 +
+ 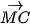 =
= 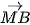 +
+ 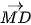
4.35. Trong mặt phẳng toạ độ Oxy, cho A(2;1), B(-2;5) và C(-5;2).
a) Tìm toạ độ của các vectơ 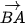 và
và 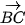 .
.
b) Chứng minh rằng A,B,C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.
c) Tìm toạ độ trọng tâm G của tam giác ABC.
d) Tìm toạ độ của điểm D sao cho tứ giác BCAD là một hình bình hành.
4.36. Trong mặt phẳng toạ độ Oxy, cho A(1;2), B(3;4), C(−1;–2) và D(6;5).
a) Tìm toạ độ của các vectơ 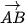 và
và 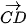 .
.
b) Hãy giải thích tại sao các vectơ 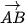
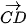 cùng phương.
cùng phương. c) Giả sử E là điểm có toạ độ (a;1). Tìm a để các vectơ 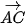 và
và 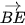 cùng phương.
cùng phương.
d) Với a tìm được, hãy biểu thị vectơ 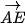 theo các vectơ
theo các vectơ 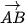
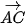 .
. 4.37. Cho vectơ  ≠
≠ 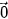 . Chứng minh rằng
. Chứng minh rằng 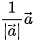 (hay còn được viết là
(hay còn được viết là 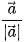
 .
. 4.38. Cho ba vectơ  ,
, 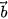 ,
, 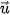 với |
với |
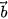 | = 1 và
| = 1 và  ⊥
⊥ 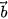 . Xét một hệ trục Oxy với các vectơ đơn vị
. Xét một hệ trục Oxy với các vectơ đơn vị 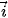 =
= 
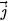 =
= 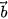 . Chứng minh rằng:
. Chứng minh rằng: a) Vectơ 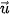 có toạ độ là (
có toạ độ là (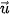 ⋅
⋅ 
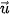 ⋅
⋅ 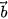 ).
). b) 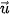 = (
= (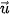 ⋅
⋅ 
 + (
+ (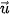 ⋅
⋅ 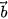 )
)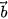 .
. 4.39. Trên sông, một ca nô chuyển động thẳng đều theo hướng S15°E với vận tốc có độ lớn bằng 20 km/h. Tính vận tốc riêng của ca nô, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.







































































Bình Luận
Để Lại Bình Luận Của Bạn