(Trang 11)
| Sau bài này em sẽ:
|
|
An được giao tìm một thiết kế mới cho bài toán tính tổng S(n) = 1 + 2 + … + n. An nhận thấy S(n) có thể được viết như sau: S(n) = 1 + 2 + … + n - 1 + n = S(n – 1) + n. Do đó, việc tính S(n) có thể được tính từ S(n – 1), tương tự S(n – 1) lại có thể được tính từ S(n – 2), cứ như vậy, cuối cùng sẽ dẫn đến cần tính S(0), nhưng S(0) = 0. Em có thể giúp An hoàn thiện ý tưởng trên thành một chương trình hay không? |
1. Ý tưởng thiết kế theo đệ quy
| Hoạt động 1 Tìm hiểu ý tưởng thiết kế thuật toán theo đệ quy Trao đổi, thảo luận và tìm hiểu ý tưởng thực hiện các tính toán sau bằng kĩ thuật đệ quy. 1. Tính tổng S(n) = 1 + 2 + … + n. 2. Tính luỹ thừa an = a x a x … x a (n lần). 3. Tính n giai thừa n! = 1 x 2 x … x n. |

Chúng ta sẽ xem xét lần lượt các bài toán trên.
a) Bài toán 1 trong Hoạt động 1
Phân tích
Bước 1. Bài toán yêu cầu tính tổng của n số nguyên từ 1 đến n. Cần thiết lập hàm S(n) trả về giá trị tổng cần tìm.
Bước 2. Điều kiện n ≥ 0. Với n = 0 ta có S(0) = 0. Đây là phần cơ sở cho điều kiện dừng của lời gọi đệ quy của hàm S(n).
Bước 3. Để thấy S(n) = n + S(n – 1) là công thức truy hồi của hàm S(n) và là cơ sở của lời gọi đệ quy của hàm.
Thuật toán 1: Hàm tính tổng.
1 def S(n):
2 if n == 0:
3 return 0
4 else:
5 return n + S(n - 1)
(Trang 12)
b) Bài toán 2 trong Hoạt động 1
Phân tích
Bước 1. Bài toán yêu cầu tính luỹ thừa a^n. Cần thiết lập hàm exp(a,n) trả về giá trị a^n.
Bước 2. Điều kiện n ≥ 0 và quy ước exp(a,0) = 1 với mọi a. Đây chính là phần cơ sở cho điều kiện dừng của lời gọi đệ quy của hàm exp(a,n).
Bước 3. Ta có an = a x an-1 suy ra exp(a,n) = a x exp(a,n-1), đây là công thức truy hồi tính exp(a,n). Từ đó có thể thiết lập lời gọi đệ quy của hàm này.
Thuật toán 2: Hàm tính luỹ thừa
1 def exp(a, n):
2 if n == 0:
3 return 1
4 else:
5 return a * exp(a, n - 1)
c) Bài toán 3 trong Hoạt động 1
Phân tích
Bước 1. Bài toán yêu cầu tính n giai thừa n!. Ta cần thiết lập hàm giaithua(n) trả về giá trị n!.
Bước 2. Điều kiện n ≥ 0 và quy ước 0! = 1, tức là giaithua(0) = 1. Đây là cơ sở cho điều kiện dừng của lời gọi đệ quy của hàm giaithua(n).
Bước 3. Ta có công thức giaithua(n) = n x giaithua(n-1), đây là công thức truy hồi tính giaithua(n). Từ đó dễ dàng thiết lập lời gọi đệ quy cho hàm này.
Thuật toán 3: Hàm tính giai thừa
1 def giaithua(n):
2 if n == 0:
3 return 1
4 else:
5 return n * giaithua(n - 1)
Nhận xét:
Cả ba bài toán trên đều có chung tính chất là từ bài toán gốc có thể đưa về trường hợp có tham số đầu vào nhỏ hơn. Điều đó sẽ dẫn đến việc có thể dừng kĩ thuật đệ quy để gọi chính hàm gốc. Nếu với các dữ liệu đầu vào nhỏ có thể giải trực tiếp (ví dụ các bài toán trên đều có lời giải cho trường hợp n = 0) thì phần cơ sở của đệ quy sẽ thực hiện lời giải trực tiếp này.
Trong cả ba chương trình trên, các hàm được định nghĩa với tham số n mặc định phải thoả mãn n ≥ 0. Do đó, các hàm này không cần có lệnh điều khiển dừng tường minh. Nhóm các lệnh cơ sở sẽ làm luôn chức năng kiểm soát dừng của lập đệ quy.
Quan sát các hàm đệ quy trên chúng ta thấy rõ tính ưu việt của kĩ thuật lập trình đệ quy, đó là tính ngắn gọn, đơn giản và dễ hiểu của chương trình.
(Trang 13)
| Ý tưởng chính của kĩ thuật đệ quy là biến đổi bài toán ban đầu về bài toán với kích thước nhỏ hơn. Nếu bài toán có kích thước nhỏ có thể giải được thì có thể thiết lập lời giải đệ quy cho bài toán này. Lời giải của các bài toán sử dụng đệ quy thường ngắn gọn và dễ hiểu. |

1. Hãy chỉ ra phần cơ sở và phần đệ quy của các chương trình trên.
2. Vì sao trong ý tưởng thiết kế đệ quy trên, yêu cầu từ bài toán với kích thước lớn cần phải đưa về cùng bài toán đó với kích thước nhỏ hơn?
2. Thuật toán tìm kiếm nhị phân
| Hoạt động 2 Thiết kế thuật toán đệ quy cho bài toán tìm kiếm nhị phân Chúng ta đã biết thuật toán tìm kiếm nhị phân trên dãy các phần tử đã sắp xếp. Hãy tìm thiết kế mới của thuật toán này theo kĩ thuật đệ quy. Trao đổi, thảo luận và trả lời các câu hỏi sau: 1. Nêu ý tưởng chính của giải thuật tìm kiếm nhị phân sử dụng đệ quy. 2. Vị trí nào trong thuật toán có thể gợi ý cho kĩ thuật đệ quy? 3. Phần cơ sở của thiết kế đệ quy nằm ở bước nào? |
![]()
Bài toán gốc của tìm kiếm nhị phân như sau:
Cho trước dãy A gồm n phần tử đã được sắp xếp theo thứ tự: A [0]≤ A[1] ≤ … ≤ A[n – 1].
Cho trước giá trị cần tìm K. Cần tìm chỉ số i của dãy A sao cho A[i] = K. Nếu tìm thấy trả về i, nếu không thấy trả về -1. Chú ý: Nếu có nhiều chỉ số thoả mãn thì chỉ cần trả về một trong số chúng.
Chúng ta nhớ lại ý tưởng chính của thuật toán tìm kiếm nhị phân.
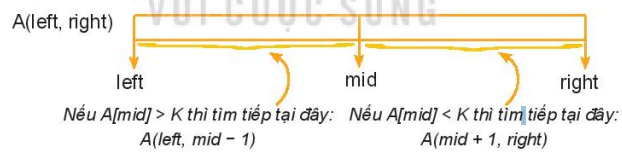
Hình 2.1. Ý tưởng của thuật toán tìm kiếm nhị phân
A(left, right)
left
mid
right
Nếu A[mid] > K thì tìm tiếp tại đây: A(left, mid - 1)
Néu A[mid] < K thì tim tiếp tại đây: A(mid + 1, right)
Các bước thực hiện tìm kiếm nhị phân như sau:
Bước 1: Đầu tiên thiết lập các biến left = 0, right = len(A) – 1.
Bước 2: Lặp liên tục cho đến khi left > right. Các bước lặp như sau:
Bước 2.1: Đặt mid = (left + right)//2
Bước 2.2: Nếu A[mid] = K thì dừng chương trình, trả về giá trị mid.
Bước 2.4: Nếu A[mid] > K thì tìm tiếp trong dãy con bên trái: A(left, mid - 1).
Bước 2.3: Nếu A[mid] < K thì tìm tiếp trong dãy con bên phải: A(mid + 1, right)
Bước 3: Nếu left > right thì dừng chương trình, trả về giá trị -1.
(Trang 14)
Theo mô tả ở trên, chúng ta thấy Bước 2.3 và Bước 2.4 thực hiện việc đưa bài toán tìm kiếm về chính bài toán đó với các dãy con có kích thước nhỏ hơn, cụ thể là bằng 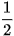
Chúng ta sẽ thiết lập hàm đệ quy cho bài toán tìm kiếm này dưới dạng:
binarySearch(A, left, right, K)
Ý nghĩa của hàm này là thực hiện tìm kiếm giá trị K trên dãy các phần tử đã sắp xếp tính từ chỉ số left đến right.
Thuật toán tìm kiếm nhị phân được mô tả bằng hàm đệ quy:
1 def binarySearch(A, left, right, K):
2 if left < right:
3 mid = (left + right)//2
4 if A[mid] == K:
5 return mid
6 elif A[mid] < K:
7 return binarySearch(A, mid + 1, right, K)
8 else:
9 return binarySearch(A, left, mid - 1, K)
10 else:
11 return -1
Lệnh gọi đệ quy cho bài toán tìm kiếm là:
binarySearch(A, 0, len(A) - 1, K)
Thuật toán tìm kiếm nhị phân có thể biểu diễn bằng kĩ thuật đệ quy trên độ dài của dãy cần tìm kiếm. Mỗi lần gọi đệ quy sẽ gọi hàm tìm kiếm trên dãy có độ dài bằng 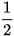 độ dài của dãy hiện tại. độ dài của dãy hiện tại. |
![]()
1. Trong chương trình trên lệnh nào đóng vai trò là phần cơ sở của đệ quy?
2. Giả sử A =[1, 3, 7, 9] và K = 10. Nếu áp dụng chương trình trên thì cần mấy lần gọi hàm đệ quy?
![]()
LUYỆN TẬP
1. Viết chương trình theo kĩ thuật đệ quy để tính hàm SL(n) là tổng các số tự nhiên lẻ nhỏ hơn hoặc bằng n.
2. Cho trước dãy A. Viết chương trình đệ quy để in dãy A theo thứ tự ngược lại.
(Trang 15)

VẬN DỤNG
1. Viết chương trình tính tổng S = 1! + 2! + … + n! theo hai cách:
a) Không sử dụng đệ quy.
b) Có sử dụng kĩ thuật đệ quy.
2. Chương trình đã biết thuật toán sắp xếp chèn trên dãy A cho trước theo hàm sau:
1 def InsertionSort(A):
2 n = len(A)
3 for i in range(1,n):
4 value = A[i]
5 j = i-1
6 while j >= 0 and A[j] > value:
7 A[j+1] = A[j]
8 j = j -1
9 A[j+1] = value
Hãy thiết kế lại chương trình trên sử dụng kĩ thuật đệ quy.
3. Bạn An đã nghĩ ra thuật toán tìm kiếm nhị phân bằng đệ quy theo cách khác như sau:
1 def binarySearch(A, left, right, K):
2 if left == right:
3 if A[left] == K:
4 return left
5 else:
6 return -1
7 else:
8 mid = (left + right)//2
9 if A[mid] == K:
10 return mid
11 elif A[mid] < K:
12 return binarySearch(A, mid + 1, right, K)
13 else:
14 return binarySearch(A, left, mid, K)
a) Chương trình của bạn An có đúng không?
b) Trong chương trình trên, phần cơ sở là những lệnh nào?









































































Bình Luận
Để Lại Bình Luận Của Bạn