Nội Dung Chính
(Trang 63)
| Sau bài này em sẽ:
|
|
Trên bàn cờ vua chúng ta đều biết Hậu là quân cờ mạnh nhất vì nó có thể di chuyển theo tất cả các hướng ngang, dọc và chéo. Một bài toán vui rất nổi tiếng là tìm cách sắp xếp 8 quân Hậu trên bàn cờ sao cho không quân Hậu nào khống chế con nào. Em hãy thử tìm một cách xếp quân Hậu khác với cách xếp như hình sau: Bài toán tìm tất cả các cách xếp n quân Hậu trên bàn cờ vua cho các quân Hậu không khống chế lẫn nhau được gọi là bài toán xếp Hậu (n-Queen Problem). Bài toán này được nhà bác học Đức Carl Friedrich Gauss nghiên cứu từ những năm 1850. Bài toán đã được mở rộng trên bàn cờ kích thước bất kì và vẫn đang được tiếp tục phát triển cho đến ngày nay.
Hình 15.1. Bàn cờ vua |
1. Mô tả bài toán xếp Hậu trên bàn cờ vua
| Hoạt động 1 Tìm hiểu mô hình bài toán xếp Hậu tổng quát. Đọc, quan sát, trao đổi và thảo luận về bài toán xếp Hậu tổng quát và cách tiếp cận quay lui để giải bài toán. |
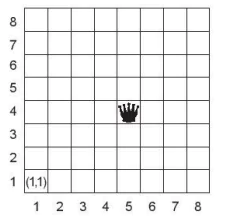
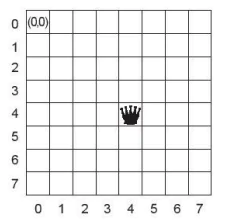
Chúng ta sẽ mô phỏng mô hình bài toán xếp Hậu tổng quát trên lưới ô vuông kích thước n × n. Trên thực tế các hàng và cột của bàn cờ Vua được đánh chỉ số từ 1 đến n, theo thứ tự từ dưới lên và từ trái sang phải. Nhưng chúng ta sẽ thiết lập lại việc đánh chỉ số từ 0 đến n – 1 và sẽ đánh số theo thứ tự từ trên xuống và từ trái sang phải.
|
Hình 15.2. Mô hình bàn cờ Vua gốc với các chỉ số hàng, cột từ 1 đến n. |
Hình 15.3. Mô hình bàn cờ Vua trên máy tính với các chỉ số hàng, cột từ 0 đến n – 1. |
(Trang 64)
Vì các quân Hậu dù có thể đặt lẫn nhau suy ra mỗi cột trên lưới ô vuông sẽ chỉ có thể có đúng một quân Hậu. Do vậy thông tin vị trí các quân Hậu có thể được cho bởi dãy n giá trị A[0], A[1], ... A[n – 1], trong đó A[k] là chỉ số hàng của quân Hậu tại cột thứ k.
Chúng ta sẽ đi tìm tất cả các nghiệm của bài toán bằng cách tìm tất cả các dãy:
A[0], A[1], ... A[n – 1]. (1)
Việc tìm kiếm này sẽ được tiến hành lần lượt tìm A[0], A[1], ... A[n – 1], đến khi số k = n – 1 thì thông báo nghiệm. Nếu không tìm được tiếp thì cần "quay lui" về vị trí biến trái để tìm tiếp. Quy trình tìm kiếm nghiệm này sẽ thực hiện theo kĩ thuật quay lui đã biết. Mệnh đề sau cho chúng ta biết cách tìm phần tử A[k] nếu đã biết các phần tử đứng trước A[0], A[1], ... A[n – 1].
Mệnh đề: Điều kiện xếp được quân Hậu tại cột thứ k.
Điều kiện để xếp được quân Hậu tại cột k là giá trị A[k] cần thoả mãn các điều kiện sau:
(i) A[k] ≠ A[j] với ∀ j < k
(ii) |A[k] – A[j]| ≠ |k – j| với ∀ j < k
Chứng minh:
– Vị quân Hậu thứ k không thể nằm trên cùng hàng với các quân Hậu nằm trên các hàng thứ A[0], A[1], ... A[n – 1], do đó điều kiện (i) hiển nhiên phải có.
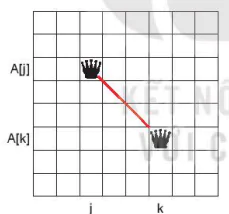
– Bây giờ chúng ta xét điều kiện để quân Hậu thứ k không thể khống chế quân Hậu thứ j theo các đường chéo là gì. Xét hai trường hợp sau:
|
Hình 15.4. Trường hợp A[j] > A[k], khi đó điều kiện để 2 quân cờ nằm trên đường chéo là A[k] – A[j] = j – k. |
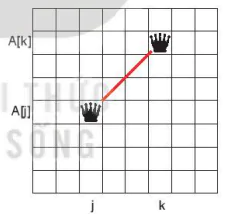
Hình 15.5. Trường hợp A[k] > A[j], khi đó điều kiện để 2 quân cờ nằm trên đường chéo là A[k] – A[j] = k – j. |
Vậy trong mọi trường hợp điều kiện để quân cờ A[k] không thể khống chế quân cờ tại vị trí A[j] là |A[k] – A[j]| ≠ |k – j|. Mệnh đề được chứng minh.
Ví dụ nếu n = 5 và A = 0 và A = 2 thì vị trí hợp lệ có thể là A = 4.
| Ý tưởng tiếp cận duyệt quay lui giải bài toán xếp Hậu tổng quát là tìm kiếm trên tất cả các dãy dạng A[0], A[1], ... A[n – 1], trong đó A[k] là chỉ số hàng của quân Hậu tại cột thứ k. |
1. Giả sử n = 4, A = 2, A = 0. Hãy tìm A.
2. Nếu n = 5, A = 0, A = 3. Tìm các khả năng của A.
2. Thiết lập lời giải bài toán xếp Hậu tổng quát
Chúng ta sẽ thiết kế thuật toán duyệt quay lui cho trường hợp tổng quát. Như vậy, số tự nhiên n được cố định trước, tập các nghiệm sẽ được tìm từ các dãy độ dài n như sau:
A[0], A[1],..., A[n - 1]
Mảng A được thiết lập trước n phần tử và bao gồm các số 0.
Thuật toán chính là trynext(k) sẽ tìm ra vị trí đầu tiên để gán cho A[k] tại thời điểm coi như đã biết vị trí k – 1 quân Hậu trước đó tại A, A, ..., A[k – 1]. Hàm này được mô tả theo mô hình tổng quát của kĩ thuật duyệt quay lui như sau:
1 def tryNext(k):
2 if k == n:
3 <Thông báo nghiệm>
4 else:
5 for i in range(n):
6 if <Có thể đặt Hậu tại hàng i cột k>:
7 A[k] = i
8 tryNext(k + 1)
Giải thích:
– Dòng 3 sẽ thông báo nghiệm nếu k = n, tức là đã tìm được đủ n vị trí A, A, ..., A[n – 1]. Hàm showQueen(A) sẽ thể hiện trên màn hình phương án sắp xếp các quân Hậu theo bộ dữ liệu của A. Chú ý các hàng sẽ đánh chỉ số từ trên xuống, các cột đánh chỉ số từ trái sang.
1 def showQueen(A):
2 n = len(A)
3 for i in range(n):
4 for j in range(n):
5 if A[i] == i:
6 print("Q", end = " ")
7 else:
8 print("0", end = " ")
9 print()
(Trang 66)
– Tại dòng 6 của tryNext(k) sẽ cần một hàm kiểm tra xem có thể đặt Hậu tại hàng i, cột k hay không, hay có thể gán A[k] = i được hay không. Hàm này để dàng thiết kế dựa trên mệnh đề đã được chứng minh trong Hoạt động 1. Hàm có tên check(A, i, j) sẽ kiểm tra và trả lại True nếu có thể gán A[k] = i và nếu ngược lại trả về False.
1 def check(A,i,j):
2 for k in range(j):
3 if A[k] == i:
4 return False
5 if abs(A[k] - i) == abs(j - k):
6 return False
7 return True
Cuối cùng nếu tất cả các hàm trên đã được thiết kế đầy đủ thì phần chương trình chính sẽ gồm các lệnh sau. Chương trình sẽ in ra màn hình tất cả các cách sắp xếp n quân Hậu trên lưới.
1 n = 8
2 A = *n
3 tryNext(0)
Chương trình hoàn chỉnh đếm và in ra tất cả các nghiệm của bài toán xếp Hậu tổng quát có thể như sau:
1 def showQueen(A):
2 n = len(A)
3 for i in range(n):
4 for j in range(n):
5 if A[j] == i:
6 print("Q", end = " ")
7 else:
8 print("0", end = " ")
9 print()
10
11 def check(A,i,j):
12 for k in range(j):
13 if A[k] == i:
14 return False
15 if abs(A[k] - i) == abs(j - k):
16 return False
17 return False
(Trang 67)
18
19 def tryNext(k):
20 global ncount
21 if k == n:
22 ncount = ncount + 1
23 print("Phương án", ncount, ":")
24 showQueen(A)
25 else:
26 for i in range(n):
27 if check(A,i,k):
28 A[k] = i
29 tryNext(k + 1)
Ví dụ muốn đếm và in ra tất cả các cách xếp quân Hậu cho bàn cờ 8 × 8 thực hiện theo các lệnh sau:
1 n = 8
2 A = *n
3 ncount = 0
4 tryNext(0)
| Lời giải bài toán tìm tất cả các phương án xếp quân Hậu trên bàn cờ Vua tổng quát n × n có thể thực hiện bằng kĩ thuật duyệt quay lui khá đơn giản. Chương trình sẽ in ra tất cả các phương án nghiệm. |
1. Với n = 3 bài toán xếp Hậu có nghiệm không?
2. Vì sao chương trình trên cần khai báo biến ncount với từ khoá global bên trong hàm tryNext()?
LUYỆN TẬP
1. Hãy tìm bằng tay (không cần máy tính) cả hai phương án của bài toán xếp Hậu với n = 4.
2. Nếu chúng ta mô phỏng lưới ô vuông đánh chỉ số các hàng từ dưới lên thì chương trình trên còn đúng không? Nếu phải thay đổi thì cần sửa chỗ nào?
VẬN DỤNG
1. Gọi Q(n) là số các cách xếp n quân Hậu lên bàn cờ kích thước n × n sao cho các quân Hậu không khống chế nhau. Sử dụng thuật toán đã được học, em hãy viết chương trình tính các giá trị Q(n) với n = 4, 5, 6, 7, 8, 9, 10.
2. Tính Q(n) với n = 11, 12, 13.
Các Bài Học Khác
Chuyên đề học tập Tin học 11 - Bài 16: Thực Hành Thiết Kế Thuật Toán Theo Kĩ Thuật Duyệt Quay Lui - Thực hành kĩ thuật duyệt quay lui giải bài toán mê cung và mở rộng các bài toán như xếp Hậu, Mã đi tuần.
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn