Nội Dung Chính
(Trang 19)
| Sau bài này em sẽ:
|
|
Năm 1883, tại một số tỉnh thành của Việt Nam và tại Pháp xuất hiện một trò chơi được quảng cáo với tên "Tháp Hà Nội" (La tour d'Hanoi). Trò chơi này được bản rộng rãi và theo một tờ quảng cáo vào thời gian đó là sẽ trao giải hàng triệu francs cho ai có thể di chuyển tất cả các mức từ tháp đến cao nhất là 64 đĩa. Trong tờ rời đó cũng đưa ra con số 18446744073709551615 bước chuyển cho trường hợp 64 đĩa và khuyên bảo rằng sẽ cần hàng tỉ năm để giải được trò chơi này. Trò chơi như sau: có ba cái cọc (ví dụ cọc 1, 2, 3) và n cái đĩa được xếp tại cọc 1 theo thứ tự từ dẫn từ trên xuống. Yêu cầu chuyển n đĩa này sang cọc 3 với điều kiện là được dùng cọc 2 làm trung gian, mỗi lần chỉ được phép chuyển 1 đĩa và không cho phép đặt đĩa to chồng lên đĩa nhỏ. Em hãy suy nghĩ và thử giải trò chơi trên với n = 1, 2.
Hình 4.1. Tờ quảng cáo trò chơi "Tháp Hà Nội", 1883. |
1. Mô tả bài toán Tháp Hà Nội
| Hoạt động 1 Tìm hiểu bài toán Tháp Hà Nội Đọc, tìm hiểu bài toán Tháp Hà Nội và thực hiện giải trò chơi này với số lượng đĩa nhỏ (1, 2, 3). Em có nhận xét gì về lời giải bài toán với n = 1, 2, 3? |
![]()
Bài toán Tháp Hà Nội do nhà bác học Pháp tên Édouard Lucas đưa ra lần đầu tiên vào năm 1883. Bài toán như sau: Cho trước ba cọc 1, 2, 3 và n cái đĩa, kí hiệu từ 1 đến n, được xếp tại cọc 1 theo thứ tự như hình dưới đây:
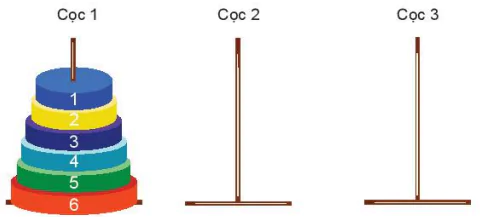
Hình 4.2. Bài toán Tháp Hà Nội
(Trang 20)
Yêu cầu: Cần chuyển n đĩa này từ cọc 1 sang cọc 3 với điều kiện sau:
– Mỗi lần chỉ được di chuyển một đĩa.
– Không được xếp đĩa to lên đĩa nhỏ hơn.
– Được phép sử dụng thêm cọc 2 làm cọc trung gian.
Với bài toán tổng quát gọi H(n) là số lần chuyển đĩa tối thiểu để giải quyết được bài toán. Quan sát các hình sau và mô tả các bước của bài toán với trường hợp n = 1, 2, 3.
Với n = 1, ta có H(1) = 1.
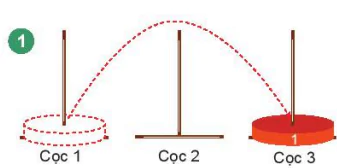
Hình 4.3. Trường hợp n = 1
Cọc 1
Cọc 2
Cọc 3
Với n = 2, ta có H(2) = 3.
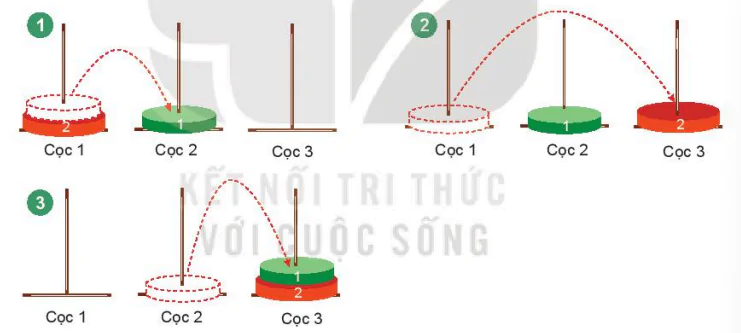
Hình 4.4. Trường hợp n = 2
Cọc 1
Cọc 2
Cọc 3
Với n = 3, ta có H(3) = 7. Quan sát lời giải sau, em có nhìn thấy quy luật gì không?
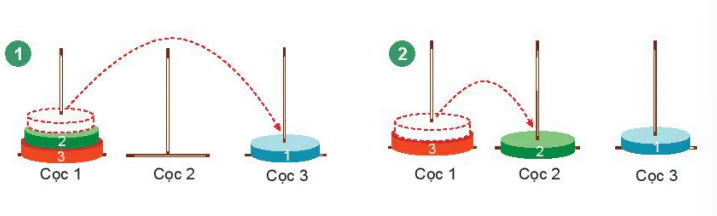
(Trang 21)
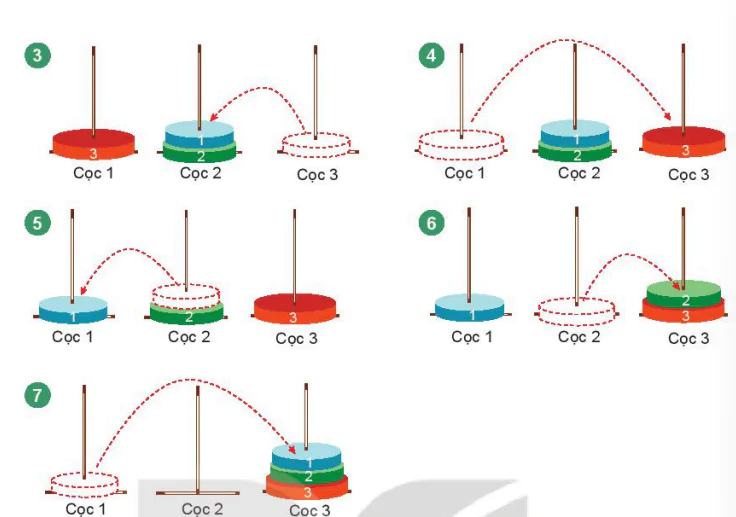
Hình 4.5. Trường hợp n = 3
Cọc 1
Cọc 2
Cọc 3
| Bài toán Tháp Hà Nội có lời giải đơn giản trong các trường hợp n = 1, 2, 3 với số lần chuyển đĩa lần lượt là 1, 3, 7. |
![]()
1. Mô tả các bước tính toán H(n) = 1, 2, 3 ở trên (không dùng hình vẽ mô tả).
2. Mô tả lời giải bài toán với n = 1, 2, 3 nếu yêu cầu là di chuyển các đĩa từ cọc 1 sang cọc 2 (cọc 3 là cọc trung gian).
2. Ý tưởng lời giải bài toán Tháp Hà Nội
| Hoạt động 2 Tìm hiểu ý tưởng thiết kế đệ quy cho lời giải bài toán Tháp Hà Nội Đọc, trao đổi để hiểu được ý tưởng thiết kế đệ quy cho lời giải bài toán Tháp Hà Nội. |
![]()
Để mô tả phép chuyển đĩa k từ cọc i đến cọc j chúng ta dùng kí hiệu sau:
k: i → j //chuyển đĩa k từ cọc i sang cọc j.
Quan sát lại các bước giải bài toán trong Hoạt động 1 và mô tả lại theo cách kí hiệu trên.
a) Trường hợp n = 1
Với n = 1, tại cọc 1 có một đĩa duy nhất, chúng ta sẽ chuyển đĩa này sang cọc 3.
1: 1 → 3 // Chuyển đĩa 1 từ cọc 1 sang cọc 3.
Như vậy, H(1) = 1.
(Trang 22)
b) Trường hợp n = 2
Với n = 2, chúng ta có hai đĩa đánh số 1, 2 tại cọc 1. Theo sơ đồ đã mô tả trong Hoạt động 1, lời giải bài toán với n = 2 sẽ như sau:
1: 1 → 2 //Chuyển đĩa 1 từ cọc 1 sang cọc 2.
2: 1 → 3 //Chuyển đĩa 2 từ cọc 1 sang cọc 3.
1: 2 → 3 //Chuyển đĩa 1 từ cọc 2 sang cọc 3.
Tổng số lần chuyển đĩa là 3, vậy H(3) = 3.
c) Trường hợp n = 3
Chúng ta có ba đĩa đánh số 1, 2, 3. Lời giải của trường hợp này sẽ sử dụng kết quả của trường hợp n = 2.
Bước 1: Chuyển 2 đĩa (đĩa 1 và 2) từ cọc 1 sang cọc 2 lấy cọc 3 làm trung gian. Việc chuyển này đưa vào trường hợp n = 2. Cụ thể sẽ cần ba thao tác như sau:
1: 1 → 3 //Chuyển đĩa 1 từ cọc 1 sang cọc 3.
2: 1 → 2 //Chuyển đĩa 2 từ cọc 1 sang cọc 2.
1: 3 → 2 //Chuyển đĩa 1 từ cọc 3 sang cọc 2.
Bước 2: Chuyển đĩa 3 từ cọc 1 sang cọc 3.
Bước 3: Chuyển 2 đĩa (đĩa 1 và 2) từ cọc 2 sang cọc 3 lấy cọc 1 làm trung gian. Việc chuyển này đưa vào trường hợp n = 2. Chú ý lúc này tại cọc 3 đã có đĩa 3, nhưng đĩa này lớn nhất nên không ảnh hưởng đến việc chuyển của hai đĩa 1 và 2. Cụ thể sẽ có ba thao tác như sau:
1: 2 → 1 //Chuyển đĩa 1 từ cọc 2 sang cọc 1.
2: 2 → 3 //Chuyển đĩa 2 từ cọc 2 sang cọc 3.
1: 1 → 3 //Chuyển đĩa 1 từ cọc 1 sang cọc 3.
Sau các bước trên việc chuyển đĩa đã hoàn thành H(3) = 7.
Nhận xét: Trong 3 bước trên, các bước 1 và 3 đều phải sử dụng lại kết quả của trường hợp n = 2, đây chính là bước áp dụng đệ quy của lời giải. Quan sát kĩ hơn lời giải của bài toán trong trường hợp n = 3, chúng ta dễ dàng tổng quát với trường hợp n bất kì.
| Ý tưởng giải bài toán Tháp Hà Nội có n đĩa từ cọc 1 sang cọc 3 như sau: Bước 1. Chuyển n – 1 đĩa từ cọc 1 sang cọc 2 lấy cọc 3 làm trung gian. Bước 2. Chuyển đĩa n từ cọc 1 sang cọc 3. Bước 3. Chuyển n – 1 đĩa từ cọc 2 sang cọc 3 lấy cọc 1 làm trung gian. |
![]()
Viết sơ đồ chi tiết giải bài toán Tháp Hà Nội cho trường hợp n = 4. Tính H(4).
3. Thiết lập chương trình giải bài toán Tháp Hà Nội
| Hoạt động 3 Thiết lập thuật toán và cài đặt chương trình cho bài toán Tháp Hà Nội Gọi Hanoi(n, i, j, k) là bài toán yêu cầu chuyển n đĩa xếp ở cọc i sang cọc j lấy cọc k làm trung gian. Các đĩa được đánh số từ 1 đến n và xếp theo thứ tự từ trên xuống. Các điều kiện của việc chuyển như sau: 1. Các đĩa đánh số từ 1 đến n và có kích thước tăng dần. 2. Mỗi lần chỉ được phép di chuyển một đĩa. 3. Không được phép xếp đĩa to lên trên đĩa nhỏ. Em hãy thiết kế thuật toán đệ quy tổng quát cho bài toán trên. Yêu cầu phải mô tả chi tiết từng bước chuyển. |
![]()
Lời giải đệ quy của bài toán Tháp Hà Nội như sau:
– Nếu n = 1 thì thực hiện chuyển đĩa 1 từ cọc i sang cọc j.
– Nếu n > 1 thì thực hiện theo ba bước như sau:
Bước 1: Chuyển n – 1 đĩa phía trên (từ 1 đến n – 1) từ cọc i sang cọc k lấy cọc j làm trung gian.
Bước 2: Chuyển đĩa n từ cọc i sang cọc j.
Bước 3: Chuyển n – 1 đĩa từ cọc k sang cọc j lấy cọc i làm trung gian.
Các bước 1 và 3 ở trên chính là lệnh gọi đệ quy đến bài toán gốc với giá trị n nhỏ hơn bài toán gốc. Có thể mô tả lời giải bài toán dưới dạng mã giả (pseudocode) như sau:
1 def Hanoi(n, i, j, k):
2 if n == 1:
3 Chuyển đĩa n từ cọc i sang cọc j
4 else:
5 Hanoi(n - 1, i, k, j)
6 Chuyển đĩa n từ cọc i sang cọc j
7 Hanoi(n - 1, k, j, i)
Từ chương trình, dễ dàng tính được công thức truy hồi số các phép chuyển đĩa của bài toán.
Với n = 1 thì H(1) = 1.
Với n > 1, các dòng lệnh 5, 6, 7 dẫn đến công thức H(n) = 2H(n – 1) + 1.
Từ các công thức trên, có thể chứng minh và tính được giá trị của H(n) = 2ⁿ – 1.
Chúng ta sẽ chuyển đổi chương trình mã giả trên thành chương trình cụ thể viết trên Python như sau:
(Trang 24)
1 def Hanoi(n, i, j, k):
2 if n == 1:
3 print("Chuyển đĩa", n, "từ cọc", i, "sang cọc", j)
4 else:
5 Hanoi(n - 1, k, j, i)
6 print("Chuyển đĩa", n, "từ cọc", i, "sang cọc", j)
7 Hanoi(n - 1, i, k, j)
Ví dụ để giải bài toán chuyển n đĩa từ cọc 1 sang cọc 3, lấy cọc 2 làm trung gian thì lệnh gọi hàm như sau:
Hanoi(n, 1, 3, 2)
| Bài toán Tháp Hà Nội tổng quát có thể giải thông qua hàm Hanoi(n, i, j, k) bằng thiết kế đệ quy. Số các phép chuyển đĩa của bài toán được tính theo công thức: H(1) = 1, H(n) = 2H(n – 1) + 1. Từ đó suy ra H(n) = 2ⁿ – 1 |

1. Tính các giá trị H(2), H(3), H(4), H(5) của bài toán Tháp Hà Nội.
2. Viết chương trình đệ quy để tính giá trị H(n) của bài toán Tháp Hà Nội.

LUYỆN TẬP
1. Viết chương trình giải bài toán Tháp Hà Nội nhưng với tên các cọc là A, B, C.
2. Viết chương trình rút gọn của hàm Hanoi(n, i, j, k) như sau và kiểm tra kết quả.
1 def Hanoi(n, i, j, k):
2 if n > 0:
3 Hanoi(n - 1, k, j, i)
4 print("Chuyển đĩa", n, "từ cọc", i, "sang cọc", j)
5 Hanoi(n - 1, k, j, i)

VẬN DỤNG
1. Hãy chứng minh công thức H(n) = 2ⁿ – 1 bằng quy nạp toán học. Hãy tính H(64) và so sánh với con số các bước đã được đưa ra trong tờ quảng cáo của trò chơi vào năm 1883.
2. Giả sử cần lưu dãy các bước chuyển đĩa của bài toán Tháp Hà Nội vào một danh sách để có thể sử dụng lại về sau. Mỗi bước chuyển dạng k: i → j sẽ được lưu trong một bộ ba số (k, i, j). Viết chương trình giải bài toán Tháp Hà Nội tổng quát Hanoi(n, i, j, k) chuyển n đĩa từ cọc i sang cọc j lấy cọc k làm trung gian với yêu cầu lưu tất cả các bước chuyển vào một danh sách (list). Như vậy, hàm Hanoi(n, i, j, k) sẽ trả về một danh sách bao gồm các bộ ba số dạng như đã mô tả ở trên.








































































Bình Luận
Để Lại Bình Luận Của Bạn