(Trang 33)
| Sau bài này em sẽ:
|
|
Trong bài học này em sẽ thiết kế lời giải cho hai bài toán sau: 1. Bài toán tính luỹ thừa exp(a, n) = an với a là số bất kì (khác 0), n là số nguyên không âm. Ở đây a0 được hiểu là tích của n lần giá trị a: an = a × a × ... × a (n lần). 2. Ban giám hiệu nhà trường cần tìm một bạn lớp em có chiều cao đúng bằng 1,7 m hoặc gần với chiều cao đó nhất để tham gia tập đội hình thể thao. Với hai bài toán trên em sẽ thực hiện như thế nào? |
1. Bài toán tính luỹ thừa
| Hoạt động 1 Giải bài toán tính luỹ thừa bằng chia để trị Hãy thiết lập thuật toán và chương trình tính luỹ thừa an với a là số bất kì khác 0, n là số nguyên không âm. |
Ví dụ an = a × an - 1 nên có thể thiết lập ngay chương trình tính hàm luỹ thừa đơn giản như sau:
Chương trình 1. Tính luỹ thừa theo cách tự nhiên.
1 def exp(a,n):
2 p = 1
3 for i in range(n):
4 p = p * a
5 return p
Phân tích.
Chương trình trên chỉ có vòng lặp tại dòng 3, lệnh thực hiện trong vòng lặp là phép nhân tại dòng 4, từ đó suy ra thời gian thực hiện chương trình là O(n).
Bây giờ chúng ta sẽ thiết lập một lời giải khác, xuất phát từ ý tưởng chia để trị. Xét các trường hợp n là chẵn hay lẻ:
+ Nếu n chẵn, tức là n = 2k ta có:
an = a2k = (ak)2 = (an/2)2
Nếu n lẻ, tức là n = 2k + 1 ta có:
an = a2k+1 = (ak)2 = (an/2)2
(Trang 34)
Từ các nhận xét trên sẽ dẫn đến công thức truy hồi để tính luỹ thừa an.
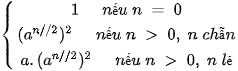
Từ công thức trên sẽ dẫn đến thuật toán sau tính exp(a, n). [2]
Chương trình 2. Tính luỹ thừa theo cách nhị phân nhanh (chia để trị).
1 def exp(a, n):
2 if n == 0:
3 return 1
4 else:
5 b = exp(a, n//2)
6 if n % 2 == 0:
7 return b * b
8 else:
9 return a * b * b
Phân tích.
Gọi T(n) là thời gian thực hiện thuật toán trên.
- Với n = 0, dòng lệnh 2 cho ta T(0) = 1.
- Tổng quát, với n bất kì, dòng 5 sẽ mất T(n/2) thời gian. Các dòng tiếp theo 7, 9 chỉ là các phép nhân ngắn, tức là chỉ mất O(1) thời gian. Vậy trong trường hợp tổng quát ta có:
T(n) = T(n/2) + O(1).
Theo cách suy luận tương tự như đối với bài toán tìm kiếm nhị phân chúng ta có ngay kết quả T(n) = O(logn), đây là bậc thời gian tốt hơn hẳn chương trình 1.
| Hàm exp(a,n) trên được thiết lập theo kĩ thuật chia để trị có độ phức tạp thời gian O(logn). |
1. Mô tả các bước tính bằng tay phép tính luỹ thừa 211 theo hai chương trình trên. Cách nào nhanh hơn?
2. Phép tính a21 sẽ cần dùng bao nhiêu phép nhân?
2. Bài toán tìm kiếm nhị phân mở rộng
| Hoạt động 2 Giải bài toán tìm kiếm nhị phân mở rộng bằng chia để trị Xây dựng thuật toán cho bài toán sau: Cho trước dãy số đã được sắp xếp tăng dần. Với giá trị K cho trước cần tìm phần tử của dãy gốc có giá trị gần với K nhất. |
(Trang 35)
Thuật toán thứ nhất dựa trên phương pháp tìm kiếm tuần tự quen thuộc đã biết. Để tìm ra phần tử của dãy gần K nhất chúng ta cần thêm các tính toán phụ tại dòng 10.
Chương trình 1. Sử dụng tìm kiếm tuần tự
1 def valueClosest(A,K):
2 n = len(A)
3 if K <= A:
4 return A
5 elif K >= A[n - 1]:
6 return A[n - 1]
7 else:
8 value = A
9 for i in range(n):
10 if abs(A[i] - K) < abs(value - K):
11 value = A[i]
12 return value
Chương trình trên hoàn toàn tương tự thuật toán tìm kiếm tuần tự, chỉ có một vòng lặp tại dòng 9, do đó có thời gian chạy O(n).
Chúng ta sẽ thiết kế thuật toán thứ hai dựa trên tìm kiếm nhị phân. Hàm đệ quy chính sẽ được thiết kế theo dạng valueClosest(A, left, right, K) sẽ tìm phần tử gần K nhất trong khoảng chỉ số từ left đến right. Trước tiên có một số nhận xét cho các trường hợp đặc biệt:
- Nếu n = 0, dãy A rỗng, hàm không có giá trị nào cần trả lại.
- Nếu n = 1, dãy A chỉ có một phần tử, khi đó hàm sẽ trả lại phần tử duy nhất của A.
- Nếu n = 2, dãy A có hai phần tử thì cần so sánh phần tử nào gần K hơn chính là phần tử cần tìm.
Trong trường hợp tổng quát, cách tìm kiếm hoàn toàn tương tự tìm kiếm nhị phân, với mỗi bước lặp sẽ gọi đệ quy với kích thước dãy giảm đi một nửa.
Chương trình cuối cùng có thể viết như sau:
Chương trình 2. Sử dụng tìm kiếm nhị phân
1 def valueClosest(A,left,right,K):
2 if left > right:
3 return
4 elif left == right:
5 return A[left]
6 elif left == right - 1:
7 if abs(A[left] - K) < abs(A[right] - K):
8 return A[left]
9 else:
10 return A[right]
11 else:
12 mid = (left + right)//2
(Trang 36)
13 if A[mid] == K:
14 return A[mid]
15 elif K < A[mid]:
16 return valueClosest(A,left,mid,K)
17 else:
18 return valueClosest(A,mid,right,K)
Lệnh gọi đệ quy là:
valueClosest(A, 0, len(A) - 1, K)
Phân tích.
- Với n = 1, dòng 4 cho ta T(n) = 1.
- Với n = 2, dòng 6 cần tính hai phép trừ và hàm abs() nên sẽ có thời gian O(1).
- Trường hợp tổng quát, các dòng lệnh từ 10 đến 16 cho ta T(n) = T(n/2) + O(1).
Sử dụng cách suy luận tương tự của tìm kiếm nhị phân ta sẽ có T(n) = O(logn).
| Thuật toán tìm kiếm nhị phân mở rộng có độ phức tạp thuật toán O(logn). |
1. Hãy giải thích kĩ hơn chương trình 2 trên tại các dòng 4 và 6.
2. Nêu những điểm khác biệt của chương trình trên với chương trình tìm kiếm nhị phân đã biết.
LUYỆN TẬP
1. Viết chương trình không đệ quy cho bài toán tìm kiếm nhị phân mở rộng trên.
2. Viết chương trình đo thời gian thực chạy để so sánh hai phương án của bài toán tìm kiếm mở rộng.
VẬN DỤNG
1. Tìm cách thiết lập thuật toán a^n theo phương pháp chia để trị nhưng không sử dụng đệ quy.
2. Bài toán tìm vùng số của dãy đã sắp xếp.
Thiết lập thuật toán chia để trị giải bài toán sau: Cho trước dãy A gồm n phần tử đã được sắp xếp theo thứ tự tăng dần, ví dụ:
A = [1, 2, 3, 3, 4, 4, 4, 5, 6, 6]
Cho trước giá trị K, cần tìm ra vùng chỉ số gồm các phần tử bằng K. Chương trình cần trả về hai chỉ số start, end là vị trí bắt đầu và kết thúc gồm toàn các giá trị K. Nếu không tìm thấy K thì phải trả về –1, –1.
Ví dụ trên, nếu K = 4 thì cần trả về hai chỉ số 4, 6.
Các Bài Học Khác
Chuyên đề học tập Tin học 11 - Bài 8: Thực Hành Thiết Kế Thuật Toán Tìm Kiếm Theo Kĩ Thuật Chia Để Trị - Thiết kế và viết chương trình tìm số lần lặp của một giá trị trong dãy đã sắp xếp bằng kĩ thuật chia để trị.
Xem thêm ⟶
Chuyên đề học tập Tin học 11 - Bài 9: Sắp Xếp Trộn - Cách thiết kế thuật toán sắp xếp trộn bằng kĩ thuật chia để trị, bao gồm thuật toán trộn hai dãy.
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn