Nội Dung Chính
(Trang 25)
| Sau bài này em sẽ:
|
|
Hãy phân tích một số ưu nhược điểm của việc áp dụng kĩ thuật đệ quy trong lập trình. |
NHIỆM VỤ 1
Thuật toán sắp xếp chèn.
Viết chương trình mô tả thuật toán sắp xếp chèn theo kĩ thuật đệ quy.
Hướng dẫn:
Chúng ta sẽ phân tích lại một lần nữa thuật toán sắp xếp chèn để tìm ra quy luật cho việc thiết lập đệ quy. Thuật toán sắp xếp chèn được mô tả ngắn gọn như sau:
1 for i in range(1,n):
2 chèn phần tử A[i] vào vị trí đúng của các phần tử A[0], A[1],..., A[i-1]
Chú ý rằng thao tác tại dòng 2 mô tả trên chỉ phụ thuộc vào các chỉ số từ 0 đến i và không phụ thuộc vào phần còn lại của dãy. Từ nhận xét này sẽ dẫn đến ý tưởng của việc thiết kế đệ quy như sau:
Giả sử gọi insertionSortRec(A,i) là thao tác tương ứng với dòng 2 của mô tả trên, khi đó chương trình trên có thể viết lại dưới dạng sau:
1 def insertionSortRec(A,i):
2 if i > 0:
3 insertionSortRec(A,i-1)
4 chèn phần tử A[i] vào vị trí đúng của các phần tử A[0], A[1],..., A[i-1]
Lệnh gọi đệ quy tại dòng 3 với điều kiện i > 0 trên sẽ đảm bảo các phần tử A[0], A[1],..., A[i-1] đã được sắp xếp đúng. Do đó việc chèn tại dòng 4 sẽ thực hiện chính xác thao tác chèn của thuật toán.
Như vậy thuật toán sắp xếp chèn có thể viết lại bằng kĩ thuật đệ quy theo hàm insertionSortRec(A,i) như sau. Chú ý các lệnh tại dòng từ 4 đến 9 chính là thao tác lỗi "chèn" của thuật toán này.
(Trang 26)
1 def insertionSortRec(A,i):
2 if i > 0:
3 insertionSortRec(A,i-1)
4 value = A[i]
5 j = i-1
6 while j >= 0 and A[j] > value:
7 A[j+1] = A[j]
8 j = j - 1
9 A[j+1] = value
Lời gọi đệ quy của hàm là:
insertionSortRec(A, len(A) - 1)
NHIỆM VỤ 2
Chuyển số thập phân sang hệ nhị phân.
Cho trước số tự nhiên n (n ≥ 0), cần đưa ra biểu diễn nhị phân của số n. Ví dụ nếu n = 11 thì kết quả phải là chuỗi nhị phân "1011".
Hướng dẫn:
Để thiết kế được chương trình này, chúng ta quan sát Bảng 5.1 mô tả các bước tính được khai triển nhị phân của một số tự nhiên n = 11.
Bảng 5.1. Các bước triển khai nhị phân n = 11
| STT | n | n//2 | n%2 |
| 1 | 11 | 5 | 1 |
| 2 | 5 | 2 | 1 |
| 3 | 2 | 1 | 0 |
| 4 | 1 | 0 | 1 |
| 5 | 0 | Số nhị phân cần tìm là 1011, dãy các số dư theo thứ tự ngược lại, từ dưới lên trên. |
Quá trình thực hiện như sau: Lần lượt biến đổi n = n//2, mỗi lần như vậy cần ghi nhớ lại số dư n%2. Quá trình kết thúc khi n = 0. Kết quả là dãy các số dư được ghép lại theo thứ tự ngược từ dưới lên.
Theo bảng trên, biểu diễn số 11 trong hệ nhị phân là "1011", trong đó kí tự cuối cùng là "1" chính là số dư 11%2, phần đầu của xâu là "101" chính là biểu diễn nhị phân của số 11//2. Gọi binary(n) là xâu biểu diễn nhị phân của số tự nhiên n. Khi đó theo cách phân tích trên chúng ta có công thức truy hồi sau:
binary(n) = binary(n//2) + str(n%2)
(Trang 27)
Lưu ý: Theo Bảng 5.1, quá trình tính số dư sẽ dừng lại khi n = 0 và có thể đặt trường hợp cơ sở là: nếu n = 0 thì hàm trả về xâu rỗng. Nhưng nếu giá trị ban đầu n = 0 thì kết quả phải là "0" nên để hoàn thiện chương trình đệ quy, chúng ta thiết lập hai trường hợp cơ sở với n = 0 và n = 1 như sau: nếu n = 1, hàm trả lại "1"; nếu n = 0, hàm trả lại "0".
Chương trình cuối cùng có thể viết như sau:
1 def binary(n):
2 if n == 0:
3 return "0"
4 elif n == 1:
5 return "1"
6 else:
7 return binary(n//2) + str(n%2)
LUYỆN TẬP
1. Viết chương trình để giải quyết nhiệm vụ 2 nhưng với yêu cầu đầu ra là hàm là một dãy (list) các số 0 và 1.
2. Viết hàm decimal(s) chuyển đổi xâu nhị phân s sang số thập phân tương ứng. Ví dụ nếu đầu vào là "10" thì kết quả 2, nếu đầu vào "1011" thì kết quả là 11. Yêu cầu viết theo kĩ thuật đệ quy.
VẬN DỤNG
1. Cho trước dãy số A =A[0], A[1].... A[n - 1].Cặp phần tử (A[i], A[j]) được gọi là nghịch đảo nếu i < j nhưng A[i] > A[j]. Viết chương trình đếm số các cặp phần tử nghịch đảo của dãy A.
a) Viết chương trình không đệ quy.
b) Viết chương trình theo kĩ thuật đệ quy.
2. Thiết kế thuật toán cho bài toán tính giá trị của đa thức dạng:
F(x) = an xn + an-1 xn-1 + ... + a1 x + a0
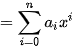
Ở đây, đầu vào là các giá trị x, a0, a1...., an
Gọi A = [a0, a1,..., an] là dãy các hệ số của đa thức (1).
Công thức (1) có thể viết lại với định nghĩa hàm F(A, x, n) như sau:
F(A, x, n) = an xn + an-1 xn-1 + ... + a1 x + a0
Các Bài Học Khác
Chuyên đề học tập Tin học 11 - Bài 4: Bài Toán Tháp Hà Nội - Trình bày lời giải bài toán Tháp Hà Nội sử dụng kĩ thuật đệ quy, mô tả các bước chuyển đĩa.
Xem thêm ⟶
Chuyên đề học tập Tin học 11 - Bài 3: Thực Hành Giải Toán Theo Kĩ Thuật Đệ Quy - Thực hành viết chương trình đệ quy giải bài toán chuyển đổi số nhị phân sang thập phân và tìm ước chung lớn nhất (ƯCLN) của hai số nguyên.
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn