Bài 21: Phương trình, bất phương trình mũ và lôgarit | Giải bài tập Toán 11 Tập 2 | Chương 6: Hàm Số Mũ Và Hàm Số Logarit - Lớp 11 - Kết Nối Tri Thức Với Cuộc Sống

Mở đầu trang 20 Toán 11 Tập 2: Giả sử giá trị còn lại (tính theo triệu đồng) của một chiếc ô tô sau t năm sử dụng được mô hình hóa bằng công thức:

V(t) = 780 ∙ (0,905)^t.

Hỏi nếu theo mô hình này, sau bao nhiêu năm sử dụng thì giá trị của chiếc ô tô đó còn lại không quá 300 triệu đồng? (Làm tròn kết quả đến hàng đơn vị).

Lời giải:

Sau bài học, ta giải được bài toán trên như sau:

Theo yêu cầu bài ra, ta cần tìm t sao cho V(t) ≤ 300

⇔ 780 ∙ (0,905)^t ≤ 300

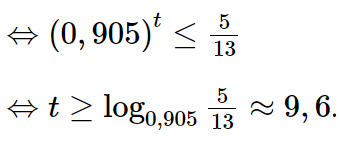
Ta có 9,6 ≈ 10. Vậy sau khoảng 10 năm sử dụng thì giá trị của chiếc ô tô đó còn lại không quá 300 triệu đồng.

1. Phương trình mũ

HĐ1 trang 20 Toán 11 Tập 2: Nhận biết nghiệm phương trình mũ

Xét phương trình:

a) Khi viết thành luỹ thừa của 2 thì phương trình trên trở thành phương trình nào?

b) So sánh số mũ của 2 ở hai vế của phương trình nhận được ở câu a để tìm x.

Lời giải:

a) Ta có . Khi đó phương trình đã cho trở thành

2^{x + 1} = 2^{– 2}. (*)

b) Vì cơ số ở vế của (*) đều bằng nhau nên số mũ phải bằng nhau, tức là

x + 1 = – 2 ⇔ x = – 3.

Luyện tập 1 trang 21 Toán 11 Tập 2: Giải các phương trình sau:

b) 2e2x = 5.

Lời giải:

Đưa vế phải về cơ số 2, ta có

Khi đó phương trình đã cho trở thành

2^{3x – 1} = 2^{– x – 1} ⇔ 3x – 1 = – x – 1 ⇔ 4x = 0 ⇔ x = 0.

Vậy phương trình đã cho có nghiệm duy nhất x = 0.

Lấy lôgarit tự nhiên hai vế của phương trình trên ta được

Vậy phương trình đã cho có nghiệm duy nhất

2. Phương trình Lôgarit

HĐ2 trang 21 Toán 11 Tập 2: Nhận biết nghiệm của phương trình lôgarit

Xét phương trình: 2log₂x = – 3.

a) Từ phương trình trên, hãy tính log₂x.

b) Từ kết quả ở câu a và sử dụng định nghĩa lôgarit, hãy tìm x.

Lời giải:

a) Ta có 2log₂x = – 3 ⇔

b) Từ định nghĩa lôgarit ta có: 

Luyện tập 2 trang 21 Toán 11 Tập 2: Giải các phương trình sau:

a) 4 – log(3 – x) = 3;

b) log₂(x + 2) + log₂(x – 1) = 1.

Lời giải:

a) 4 – log(3 – x) = 3

Điều kiện: 3 – x > 0 ⇔ x < 3.

Phương trình đã cho trở thành log(3 – x) = 1 ⇔ 3 – x = 101 ⇔ x = – 7 (t/m).

Vậy phương trình đã cho có nghiệm duy nhất x = – 7.

b) log₂(x + 2) + log₂(x – 1) = 1

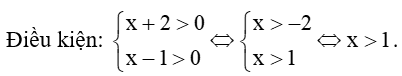
Áp dụng tính chất của lôgarit, phương trình đã cho trở thành

log₂ [(x + 2)(x – 1)] = 1

⇔ (x + 2)(x – 1) = 2¹

⇔ x² + x – 2 = 2

⇔ x² + x – 4 = 0

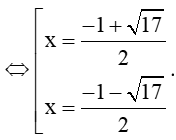
Kết hợp với điều kiện, vậy phương trình đã cho có nghiệm duy nhất

3. Bất phương trình mũ

HĐ3 trang 22 Toán 11 Tập 2: Nhận biết nghiệm của bất phương trình mũ

Cho đồ thị của các hàm số y = 2^x và y = 4 như Hình 6.7. Tìm khoảng giá trị của x mà đồ thị hàm số y = 2^x nằm phía trên đường thẳng y = 4 và từ đó suy ra tập nghiệm của bất phương trình 2^x > 4.

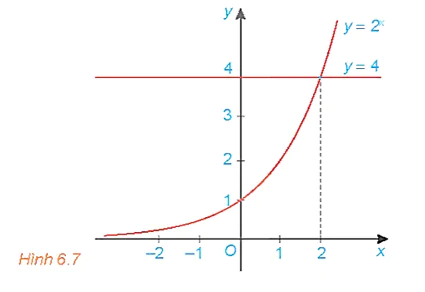
Lời giải:

Quan sát đồ thị Hình 6.7, ta thấy khoảng giá trị của x mà đồ thị hàm số y = 2^x nằm phía trên đường thẳng y = 4 là (2; + ∞).

Vậy tập nghiệm của bất phương trình 2^x > 4 là (2; + ∞).

Luyện tập 3 trang 23 Toán 11 Tập 2: Giải các bất phương trình sau:

a) 0,1^{2x – 1} ≤ 0,1^{2 – x};

b) 3 ∙ 2^{x + 1} ≤ 1.

Lời giải:

a) Ta có:

0,1^{2x – 1} ≤ 0,1^{2 – x}

⇔ 2x – 1 ≥ 2 – x (do 0 < 0,1 < 1)

⇔ 3x ≥ 3

⇔ x ≥ 1.

Vậy tập nghiệm của bất phương trình đã cho là [1; + ∞).

4. Bất phương trình Lôgarit

HĐ4 trang 23 Toán 11 Tập 2: Nhận biết nghiệm của bất phương trình lôgarit

Cho đồ thị của các hàm số y = log₂x và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số y = log₂x nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình log₂ x > 2.

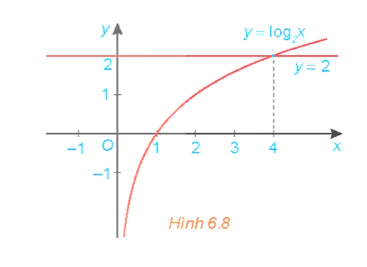
Lời giải:

Quan sát đồ thị ở Hình 6.8, ta thấy khoảng giá trị của x mà đồ thị hàm số y = log₂x nằm phía trên đường thẳng y = 2 là (4; + ∞).

Vậy tập nghiệm của bất phương trình log₂ x > 2 là (4; + ∞).

Luyện tập 4 trang 24 Toán 11 Tập 2: Giải các bất phương trình sau:

b) 2log(2x + 1) > 3.

Lời giải:

Bất phương trình đã cho tương đương với 

log_7⁻¹(x+1) > log₇(2−x)

⇔ – log₇­(x + 1) > log₇(2 – x)

⇔ log₇(x + 1)^{– 1} > log₇(2 – x)

⇔ (x + 1)^{– 1} > 2 – x (do 7 > 1).

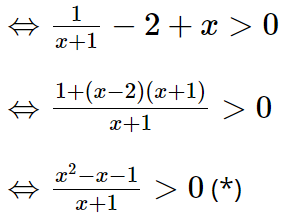
Mà – 1 < x < 2 nên x + 1 > 0, do đó (*) ⇔ x² – x – 1 > 0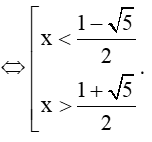

Kết hợp với điều kiện ta được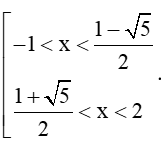

Vậy tập nghiệm của bất phương trình đã cho là

Vận dụng trang 24 Toán 11 Tập 2: Áp suất khí quyển p (tính bằng kilôpascan, viết tắt là kPa) ở độ cao h (so với mực nước biển, tính bằng km) được tính theo công thức sau:

(Theo britannica.com)

a) Tính áp suất khí quyển ở độ cao 4 km.

b) Ở độ cao trên 10 km thì áp suất khí quyển sẽ như thế nào?

Lời giải:

a) Ở độ cao 4 km, tức h = 4, thay vào công thức đã cho ta được

Vậy áp suất khí quyển ở độ cao 4 km khoảng 56,47 kPa.

b) Ở độ cao trên 10 km, tức h > 10, khi đó ta có

Vậy ở độ cao trên 10 km thì áp suất khí quyển nhỏ hơn 23,97 kPa.