Bài 33: Đạo hàm cấp hai | Giải bài tập Toán 11 Tập 2 | Chương 9: Đạo Hàm - Lớp 11 - Kết Nối Tri Thức Với Cuộc Sống

Mở đầu trang 95 Toán 11 Tập 2: Chuyển động của một vật gắn trên con lắc lò xo (khi bỏ qua ma sát và sức cản không khí) được cho bởi phương trình sau:

ở đó x tính bằng centimet và thời gian t tính bằng giây. Tìm gia tốc tức thời của vật tại thời điểm t = 5 giây (làm tròn kết quả đến hàng đơn vị).

Lời giải:

Vận tốc của vật tại thời điểm t là

Gia tốc tức thời của vật tại thời điểm t là:

Tại thời điểm t = 5, gia tốc của vật là:

1. Khái niệm đạo hàm cấp hai

HĐ1 trang 95 Toán 11 Tập 2: Nhận biết đạo hàm cấp hai của một hàm số

a) Gọi g(x) là đạo hàm của hàm số Tìm g(x).

b) Tính đạo hàm của hàm số y = g(x).

Lời giải:

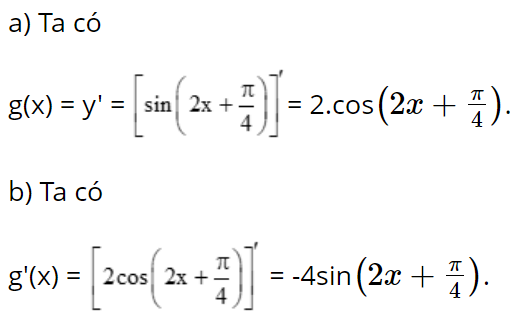
Luyện tập 1 trang 95 Toán 11 Tập 2: Tính đạo hàm cấp hai của các hàm số sau:

a) y = xe^2x;

b) y = ln(2x + 3).

Lời giải:

a) Ta có y = xe^2x

Suy ra: y' = x' . e^2x + x . (e^2x)' = e^2x + 2xe^2x.

Do đó, y'' = 2e^2x + 2(e^2x + 2xe^2x) = 2e^2x + 2e^2x + 4xe^2x = 4e^2x + 4xe^2x.

Vậy đạo hàm cấp hai của hàm số đã cho là y'' = 4e^2x + 4xe^2x.

b) Ta có y = ln(2x + 3).

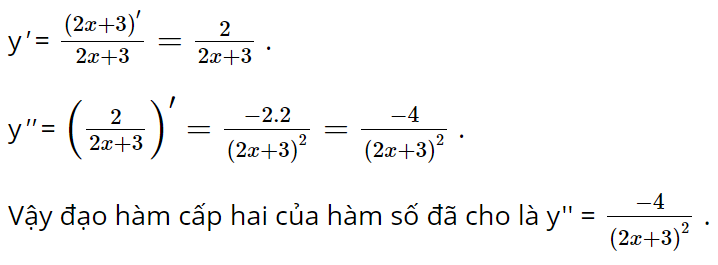
2. Ý nghĩa cơ học của đạo hàm cấp hai

HĐ2 trang 96 Toán 11 Tập 2: Nhận biết ý nghĩa cơ học của đạo hàm cấp hai

Xét một chuyển động có phương trình s = 4cos2πt.

a) Tính vận tốc tức thời của chuyển động tại thời điểm t.

b) Tính gia tốc tức thời tại thời điểm t.

Lời giải:

a)

Ta có: v(t) = s'(t) = –4.2πsin2πt = –8πsin2πt.

Vậy vận tốc tức thời của chuyển động tại thời điểm t là –8πsin2πt.

b) Gia tốc tức thời tại thời điểm t là

a(t) = v'(t) = (–8πsin2πt)' = –8π.2πcos2πt = –16π²cos2πt.

Vận dụng trang 96 Toán 11 Tập 2: Một chuyển động thẳng có phương trình (s tính bằng mét, t tính bằng giây). Tìm gia tốc của vật tại thời điểm t = 4 giây.

Lời giải:

Vận tốc tại thời điểm t là v(t) = s'(t) = 4t + 2t³.

Gia tốc tức thời của vật tại thời điểm t là a(t) = v'(t) = 4 + 6t².

Tại thời điểm t = 4 giây, gia tốc của vật là:

a(4) = 4 + 6 . 4² = 100 (m/s²).