Nội Dung Chính
(Trang 30)
Sau điểm và vectơ, những đối tượng khác của hình học phẳng như đường thẳng, đường tròn, ... sẽ lần lượt được đại số hoá ở chương này. Đối với mỗi đối tượng hình học đó, trước hết ta đưa ra đối tượng đại số tương ứng, được gọi là phương trình của nó. Các mối quan hệ, công thức tính toán hình học sẽ được thể hiện theo các yếu tố của phương trình tương ứng.
Nhờ đại số hóa hình học, ta có thể dùng ngôn ngữ và phương pháp của đại số để diễn đạt và học tập hình học. Ngoài ra, đại số hoá hình học là bước quan trọng cho phép ta dùng ngôn ngữ của máy tính để diễn đạt hình học. Nhờ đó, ta có thể sử dụng công nghệ thông tin trong học tập và áp dụng hình học, chẳng hạn, các phần mềm vẽ hình như GeoGebra (dùng trong học tập), Autocad (dùng trong vẽ thiết kế) đều sử dụng các kiến thức hình học.
| THUẬT NGỮ • Vectơ chỉ phương • Vectơ pháp tuyến • Phương trình tổng quát • Phương trình tham số | KIẾN THỨC, KĨ NĂNG • Mô tả phương trình tổng quát và phương trình tham số của đường thẳng. • Lập phương trình của đường thẳng khi biết một điểm và một vectơ pháp tuyến hoặc một điểm và một vectơ chỉ phương hoặc hai điểm. • Giải thích mối liên hệ giữa đồ thị hàm bậc nhất và đường thẳng. • Vận dụng kiến thức về phương trình đường thẳng để giải một số bài toán có liên quan đến thực tiễn. |
Đường thẳng là một tập hợp điểm, được xác định bởi tính chất đặc trưng của các điểm thuộc đường thẳng đó. Do vậy, ta có thể đại số hoá đường thẳng bằng cách thể hiện tính chất đặc trưng đó bởi điều kiện đại số đối với toạ độ của các điểm tương ứng.
(Trang 31)
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG
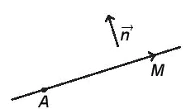
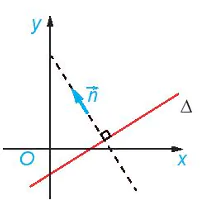
| HĐ1. Cho vectơ 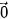 và điểm A. Tìm tập hợp những điểm M sao cho và điểm A. Tìm tập hợp những điểm M sao cho 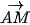 vuông góc với vuông góc với 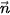 . .
|
Hình 7.1a
Hình 7.1b |
Nhận xét
• Nếu 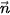
 thì k
thì k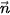 (k ≠ 0) cũng là vectơ pháp tuyến của
(k ≠ 0) cũng là vectơ pháp tuyến của  .
. • Đường thẳng hoàn toàn xác định nếu biết một điểm và một vectơ pháp tuyến của nó.
Ví dụ 1. Trong mặt phẳng toạ độ, cho tam giác có ba đỉnh là A( 3; 1), B(4; 0), C(5; 3). Hãy chỉ ra một vectơ pháp tuyến của đường trung trực của đoạn thẳng AB và một vectơ pháp tuyến của đường cao kẻ từ A của tam giác ABC.
Giải
Đường trung trực của đoạn thẳng AB vuông góc với AB nên có vectơ pháp tuyến 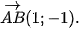
Đường cao kẻ từ A của tam giác ABC vuông góc với BC nên có vectơ pháp tuyến 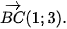
HĐ2. Trong mặt phẳng toạ độ, cho đường thẳng  đi qua điểm
đi qua điểm 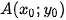 và có vectơ pháp tuyến
và có vectơ pháp tuyến 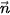 (a; b). Chứng minh rằng điểm M(x; y) thuộc
(a; b). Chứng minh rằng điểm M(x; y) thuộc  khi và chỉ khi
khi và chỉ khi
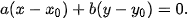 | (1) |
Nhận xét
Trong HĐ2, nếu đặt 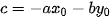 thì (1) còn được viết dưới dạng ax + by +c=0 và được gọi là phương trình tổng quát của
thì (1) còn được viết dưới dạng ax + by +c=0 và được gọi là phương trình tổng quát của  . Như vậy, điểm M(x; y) thuộc đường thẳng
. Như vậy, điểm M(x; y) thuộc đường thẳng  khi và chỉ khi toạ độ của nó thoả mãn phương trình tổng quát của
khi và chỉ khi toạ độ của nó thoả mãn phương trình tổng quát của  .
.
Trong mặt phẳng toạ độ, mọi đường thẳng đều có phương trình tổng quát dạng ax + by + c = 0, với a và b không đồng thời bằng 0. Ngược lại, mỗi phương trình dạng ax + by + c = 0, với a và b không đồng thời bằng 0, đều là phương trình của một đường thẳng, nhận 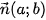 |
Ví dụ 2. Trong mặt phẳng toạ độ, lập phương trình tổng quát của đường thẳng  đi qua điểm A(2; 1) và nhận
đi qua điểm A(2; 1) và nhận 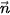 (3; 4) là một vectơ pháp tuyến.
(3; 4) là một vectơ pháp tuyến.
Giải
Đường thẳng  có phương trình là 3(x – 2)+ 4(y – 1)= 0 hay 3x + 4y – 10=0.
có phương trình là 3(x – 2)+ 4(y – 1)= 0 hay 3x + 4y – 10=0.
(Trang 32)
Luyện tập 1. Trong mặt phẳng toạ độ, cho tam giác có ba đỉnh A(−1; 5), B(2; 3), C(6; 1). Lập phương trình tổng quát của đường cao kẻ từ A của tam giác ABC.
Ví dụ 3. Trong mặt phẳng toạ độ, lập phương trình đường thẳng  đi qua điểm A(0; b) và có vectơ pháp tuyến
đi qua điểm A(0; b) và có vectơ pháp tuyến 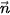
 có mối liên hệ gì với đồ thị của hàm số y = ax + b.
có mối liên hệ gì với đồ thị của hàm số y = ax + b. Giải
Đường thẳng  có phương trình là a(x – 0) – 1(y – b) = 0 hay ax − y + b = 0.
có phương trình là a(x – 0) – 1(y – b) = 0 hay ax − y + b = 0.
Đường thẳng  là tập hợp những điểm M(x; y) thoả mãn ax − y + b = 0 (hay là, y = ax + b).
là tập hợp những điểm M(x; y) thoả mãn ax − y + b = 0 (hay là, y = ax + b).
b) Do đó, đồ thị của hàm số y = ax + b chính là đường thẳng  : ax − y + b = 0.
: ax − y + b = 0.
Luyện tập 2. Hãy chỉ ra một vec tơ pháp tuyến của đường thẳng 
Nhận xét. Trong mặt phẳng toạ độ, cho đường thẳng  : ax + by + c = 0.
: ax + by + c = 0.
• Nếu b = 0 thì phương trình  có thể đưa về dạng x = m (với
có thể đưa về dạng x = m (với 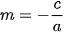 ) và
) và  vuông góc với Ox.
vuông góc với Ox.
• Nếu b≠ 0 thì phương trình 
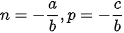 ).
). 2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
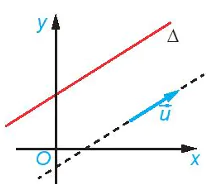
| HĐ3. Trong Hình 7.2a, nếu một vật thể chuyển động với vectơ vận tốc bằng
Nhận xét • Nếu • Đường thẳng hoàn toàn xác định nếu biết một điểm và một vectơ chỉ phương của nó. • Hai vecto |
Hình 7.2a
Hình 7.2b |
Ví dụ 4. Trong mặt phẳng toạ độ, cho A(3; 2), B(1;– 4). Hãy chỉ ra hai vectơ chỉ phương của đường thẳng AB.
Giải
Đường thẳng AB nhận 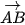 (2;– 6) là một vectơ chỉ phương.
(2;– 6) là một vectơ chỉ phương.
Lấy 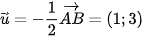 , khi đó
, khi đó 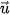
(Trang 33)
Luyện tập 3. Hãy chỉ ra một vectơ chỉ phương của đường thẳng  : 2x−y+1=0.
: 2x−y+1=0.
HĐ4. Chuyển động của một vật thể được thể hiện trên mặt phẳng Oxy. Vật thể khởi hành từ A(2; 1) và chuyển động thẳng đều với vectơ vận tốc là 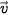 (3; 4).
(3; 4).
a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm đi qua và vectơ chỉ phương của đường thẳng đó)?
b) Chứng minh rằng, tại thời điểm t (t > 0) tính từ khi khởi hành, vật thể ở vị trí có toạ độ là (2+3t; 1+ 4t).
| Cho đường thẳng  khi và chỉ khi tồn tại số thực t sao cho khi và chỉ khi tồn tại số thực t sao cho 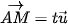 , hay , hay
Hệ (2) được gọi là phương trình tham số của đường thẳng |
Ví dụ 5. Lập phương trình tham số của đường thẳng 
chỉ phương
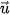 (4;−1).
(4;−1). Giải
Phương trình tham số của đường thẳng  là
là
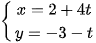
Luyện tập 4. Lập phương trình tham số của đường thẳng  đi qua điểm M(−1; 2) và song song với đường thẳng d : 3x – 4y−1=0.
đi qua điểm M(−1; 2) và song song với đường thẳng d : 3x – 4y−1=0.
Ví dụ 6. Lập phương trình tham số của đường thẳng đi qua hai điểm A(2; 3) và B(1; 5).
Giải
Đường thẳng AB đi qua A(2; 3) và có vectơ chỉ phương 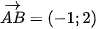
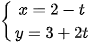
Luyện tập 5. Lập phương trình tham số và phương trình tổng quát của đường thẳng đi qua hai điểm phân biệt 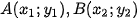 ) cho trước.
) cho trước.
(Trang 34)
| Vận dụng. Việc quy đổi nhiệt độ giữa đơn vị độ C (Anders Celsius, 1 701 – 1744) và đơn vị độ F (Daniel Fahrenheit, 1 686 – 1 736) được xác định bởi hai mốc sau: Nước đóng băng ở 0°C, 32°F; Nước sôi ở 100°C, 212°F. Trong quy đổi đó, nếu a°C tương ứng với b°F thì trên mặt phẳng toạ độ Oxy, điểm M(a, b) thuộc đường thẳng đi qua A(0; 32) và B(100; 212). Hỏi 0°F, 100°F tương ứng với bao nhiêu độ C? |
Nhiệt kế dùng hai đơn vị đo là độ F và độ C |
BÀI TẬP
7.1. Trong mặt phẳng toạ độ, cho 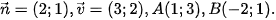
a) Lập phương trình tổng quát của đường thẳng 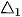
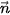 .
. b) Lập phương trình tham số của đường thẳng 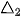 đi qua B và có vectơ chỉ phương
đi qua B và có vectơ chỉ phương 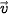 .
.
c) Lập phương trình tham số của đường thẳng AB.
7.2. Lập phương trình tổng quát của các trục toạ độ.
7.3. Cho hai đường thẳng  :
: 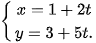
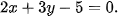
a) Lập phương trình tổng quát của 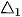 .
.
b) Lập phương trình tham số của 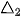 .
.
7.4. Trong mặt phẳng toạ độ, cho tam giác ABC có A(1, 2), B(3; 0) và C(-2;-1).
a) Lập phương trình đường cao kẻ từ A.
b) Lập phương trình đường trung tuyến kẻ từ B.
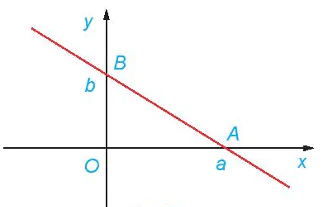
7.5. (Phương trình đoạn chắn của đường thẳng) Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab≠0 (H.7.3) có phương trình là 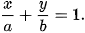 |
Hình 7.3 |
7.6. Theo Google Maps, sân bay Nội Bài có vĩ độ 21,2° Bắc, kinh độ 105,8° Đông, sân bay Đà Nẵng có vĩ độ 16,1° Bắc, kinh độ 108,2° Đông. Một máy bay, bay từ Nội Bài đến sân bay Đà Nẵng. Tại thời điểm t giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ x° Bắc, kinh độ y° Đông được tính theo công thức
(Trang 35)
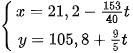
a) Hỏi chuyến bay từ Hà Nội đến Đà Nẵng mất mấy giờ?
b) Tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến 17 (17° Bắc) chưa?
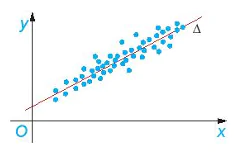
| Em có biết? Hồi quy tuyến tính là một phương pháp được sử dụng trong thống kê để dự báo về mối quan hệ giữa các đại lượng dựa trên kết quả thống kê mẫu. Chẳng hạn, để dự báo về mối quan hệ giữa hai đại lượng x và y (y phụ thuộc vào x như thế nào), từ kết quả thống kê được thể hiện ở Hình 7.4a, phương pháp hồi quy tuyến tính đưa ra đường thẳng Để xác định  đến M' đến M' . Khi đó, a, b được chọn sao cho tổng các bình phương này là nhỏ nhất. . Khi đó, a, b được chọn sao cho tổng các bình phương này là nhỏ nhất. Nhờ đưa ra được đường thẳng biểu thị (gần đúng) sự phụ thuộc giữa đại lượng y theo đại lượng x, người ta có thể đưa ra các dự báo nằm ngoài kết quả thống kê. Tất nhiên, không phải mô hình nào cũng phù hợp với phương pháp này, ngay cả khi kết quả thống kê tập trung dọc một đường thẳng. Chẳng hạn, để xác định đường đi của một quả tên lửa, nếu dựa vào một số quan sát ban đầu để dự đoán, ta có thể nghĩ rằng nó chuyển động thẳng, nhưng trên thực tế, nhìn chung nó đi theo đường parabol. Sai lầm trong những dự báo như vậy thật là tai hại!
Hình 7.4 |
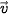 và đi qua A thì nó di chuyển trên đường nào?
và đi qua A thì nó di chuyển trên đường nào? được gọi là vectơ chỉ phương của đường thẳng
được gọi là vectơ chỉ phương của đường thẳng 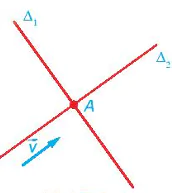
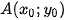 và có vectơ chỉ phương
và có vectơ chỉ phương 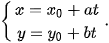

 (H.7.4b) thể hiện gần đúng nhất mối quan hệ giữa các đại lượng x và y đã được thống kê. Về mặt hình ảnh, các chấm xanh trên hình vẽ (có toạ độ là các cặp giá trị (x; y) trong kết quả thống kê, tập trung dọc theo
(H.7.4b) thể hiện gần đúng nhất mối quan hệ giữa các đại lượng x và y đã được thống kê. Về mặt hình ảnh, các chấm xanh trên hình vẽ (có toạ độ là các cặp giá trị (x; y) trong kết quả thống kê, tập trung dọc theo 







































































Bình Luận
Để Lại Bình Luận Của Bạn