(Trang 43)
| THUẬT NGỮ • Đường tròn • Tâm • Bán kính • Phương trình đường tròn • Phương trình tiếp tuyến | KIẾN THỨC, KĨ NĂNG • Lập phương trình đường tròn khi biết toạ độ tâm và bán kính hoặc biết toạ độ ba điểm thuộc đường tròn. • Xác định tâm và bán kính của đường tròn khi biết phương trình của nó. • Lập phương trình tiếp tuyến của đường tròn khi biết toạ độ của tiếp điểm. • Vận dụng kiến thức về phương trình đường tròn để giải một số bài toán liên quan đến thực tiễn. |
Cũng như đối với đường thẳng, việc đại số hoá đường tròn gồm hai bước.
• Thiết lập đối tượng đại số tương ứng với đường tròn, gọi là phương trình của đường tròn.
• Chuyển các yếu tố liên quan tới đường tròn từ hình học sang đại số.
1. PHƯƠNG TRÌNH ĐƯỜNG TRÒN
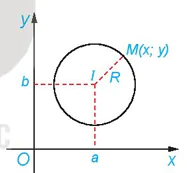
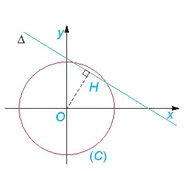
| Đường tròn tâm I, bán kính R là tập hợp những điểm M thoả mãn điều kiện IM = R. Do đó, để lập phương trình đường tròn đó, ta cần chuyển điều kiện hình học IM = R thành một điều kiện đại số. HĐ1. Trong mặt phẳng toạ độ Oxy, cho đường tròn (C), tâm I(a, b), bán kính R (H.7.13). Khi đó, một điểm M(x; y) thuộc đường tròn (C) khi và chỉ khi toạ độ của nó thoả mãn điều kiện đại số nào? |
Hình 7.13 |
Điểm M(x; y) thuộc đường tròn (C), tâm I(a, b), bán kính R khi và chỉ khi
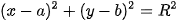 | (1) |
Ta gọi (1) là phương trình của đường tròn (C).
Ví dụ 1. Tìm tâm và bán kính của đường tròn (C) có phương trình: 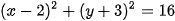 .
.
Viết phương trình đường tròn (C') có tâm J(2; – 1) và có bán kính gấp đôi bán kính đường tròn (C).
Giải
Ta viết phương trình của (C) ở dạng 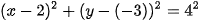 .
.
Vậy (C) có tâm I = (2;−3) và bán kính R= 4.
Đường tròn (C') có tâm J (2; – 1) và có bán kính R' = 2R= 8, nên có phương trình
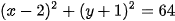
(Trang 44)
Luyện tập 1. Tìm tâm và bán kính của đường tròn (C): 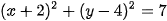
Nhận xét. Phương trình (1) tương đương với
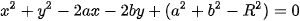
Ví dụ 2. Cho a, b, c là các hằng số. Tìm tập hợp những điểm M(x; y) thoả mãn phương trình
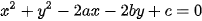 | (2) |
Giải
Phương trình (2) tương đương với
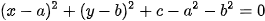
⇔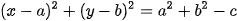 .
.
Xét I(a, b), khi đó, IM = 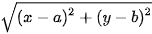
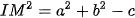 | (3) |
Từ đó, ta xét các trường hợp sau:
- Nếu 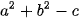 > 0 thì tập hợp những điểm M thoả mãn (2) là đường tròn tâm I(a, b), bán kính
> 0 thì tập hợp những điểm M thoả mãn (2) là đường tròn tâm I(a, b), bán kính 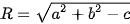 .
.
- Nếu 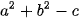 = 0 thì (3) ⇔ IM =0. Do đó, tập hợp những điểm M thoả mãn (2) chỉ gồm một điểm là l(a, b).
= 0 thì (3) ⇔ IM =0. Do đó, tập hợp những điểm M thoả mãn (2) chỉ gồm một điểm là l(a, b).
- Nếu 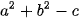
| Phương trình là phương trình của một đường tròn (C) khi và chỉ khi |
Luyện tập 2. Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng.
a) 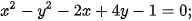
b) 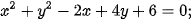
c) 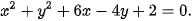
Ví dụ 3. Viết phương trình đường tròn (C) đi qua ba điểm A(2; 0), B(0; 4), C(−7; 3).
Giải
Các đoạn thẳng AB, AC tương ứng có trung điểm là M(1;2), N 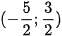 . Đường thẳng trung trực
. Đường thẳng trung trực  của đoạn thẳng AB đi qua M(1; 2) và có vectơ pháp tuyến
của đoạn thẳng AB đi qua M(1; 2) và có vectơ pháp tuyến 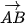 (-2; 4).
(-2; 4).
Vì 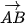
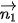 (1; – 2) nên
(1; – 2) nên 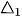 cũng nhận
cũng nhận 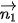 (1; – 2) là vectơ pháp tuyến.
(1; – 2) là vectơ pháp tuyến. Do đó, phương trình của 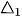 là
là
1(x-1)-2(x-2)=0 hay x-2y+3=0.
(Trang 45)
Đường thẳng trung trực 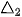
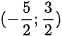 và có vectơ pháp tuyến
và có vectơ pháp tuyến 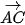 (-9; 3).
(-9; 3). Vì 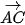 (–9; 3) cùng phương với
(–9; 3) cùng phương với  (3; -1) nên
(3; -1) nên 
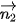 (3; -1) là vectơ pháp tuyến.
(3; -1) là vectơ pháp tuyến. Do đó, phương trình của 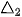 là
là
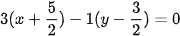
hay 3x-y+9=0.
Tâm I của đường tròn (C) cách đều ba điểm A, B, C nên I là giao điểm của 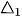 và
và 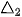
Vậy toạ độ của I là nghiệm của hệ phương trình 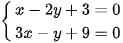 .
.
Suy ra I(–3; 0). Đường tròn (C) có bán kính là IA = 5. Vậy phương trình của (C) là
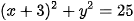
Luyện tập 3. Viết phương trình đường tròn (C) đi qua ba điểm M(4; –5), N(2; −1), P(3; –8).
| Vận dụng. Bên trong một hồ bơi, người ta dự định thiết kế hai bể sục nửa hình tròn bằng nhau và một bể sục hình tròn (H.7.14) để người bơi có thể ngồi tựa lưng vào thành các bể sục thư giãn. Hãy tìm bán kính của các bể sục để tổng chu vi của ba bể là 32 m mà tổng diện tích (chiếm hồ bơi) là nhỏ nhất. Trong tính toán, lấy Hướng dẫn - Gọi bán kính bể hình tròn và bể nửa hình tròn tương ứng là x, y (m). Khi đó, tổng chu vi ba bể là 32 m khi và chỉ khi 1,57x+2,57y-8=0. - Gọi tổng diện tích của ba bể sục là S (m
- Trong mặt phẳng toạ độ Oxy, xét đường tròn (C):
|
Hình 7.14
Hình 7.15 |
(Trang 46)
2. PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
| HĐ2. Cho đường tròn (C): a) Chứng minh điểm M(4; –2) thuộc đường tròn (C). b) Xác định tâm và bán kính của (C). c) Gọi |
Hình 7.16 |
| Cho điểm M 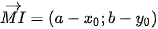 và phương trình và phương trình
|
Ví dụ 4. Cho đường tròn (C) có phương trình 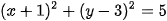 . Điểm M(0; 1) có thuộc đường tròn (C) hay không? Nếu có, hãy viết phương trình tiếp tuyến tại M của (C).
. Điểm M(0; 1) có thuộc đường tròn (C) hay không? Nếu có, hãy viết phương trình tiếp tuyến tại M của (C).
Giải
Do 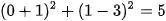 nên điểm M thuộc (C).
nên điểm M thuộc (C).
Đường tròn (C) có tâm là I(−1; 3). Tiếp tuyến của (C) tại M(0; 1) có vectơ pháp tuyến 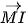
-1(x-0)+2(y-1)=0 ⇔ x-2y+2=0.
Luyện tập 4. Cho đường tròn (C): 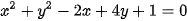 . Viết phương trình tiếp tuyến
. Viết phương trình tiếp tuyến  của (C) tại điểm N(1; 0).
của (C) tại điểm N(1; 0).
BÀI TẬP
7.13. Tìm tâm và tính bán kính của đường tròn
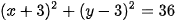
7.14. Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng.
a) 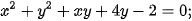
b) 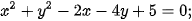
c) 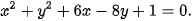
(Trang 47)
7.15. Viết phương trình của đường tròn (C) trong mỗi trường hợp sau:
a) Có tâm I(–2; 5) và bán kính R = 7;
b) Có tâm I(1; −2) và đi qua điểm A(-2; 2);
c) Có đường kính AB, với A(−1; –3), B(–3; 5);
d) Có tâm I(1; 3) và tiếp xúc với đường thẳng x + 2y +3=0.
7.16. Trong mặt phẳng toạ độ, cho tam giác ABC, với A(6; −2), B(4; 2), C(5 –5).
Viết phương trình đường tròn ngoại tiếp tam giác đó.
7.17. Cho đường tròn (C): 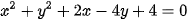 . Viết phương trình tiếp tuyến d của (C) tại điểm M(0; 2).
. Viết phương trình tiếp tuyến d của (C) tại điểm M(0; 2).
7.18. Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng toạ độ. Theo đó, tại thời điểm t (0 ≤t≤180) vật thể ở vị trí có toạ độ 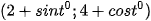 .
.
a) Tìm vị trí ban đầu và vị trí kết thúc của vật thể.
b) Tìm quỹ đạo chuyển động của vật thể.
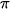 = 3,14, độ dài tính theo mét và làm tròn tới chữ số thập phân thứ hai.
= 3,14, độ dài tính theo mét và làm tròn tới chữ số thập phân thứ hai.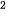 ). Khi đó
). Khi đó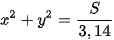
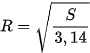 và đường thẳng
và đường thẳng 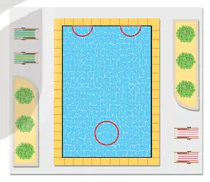
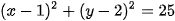 và điểm M(4; -2).
và điểm M(4; -2).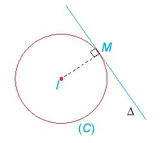
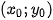 thuộc đường tròn (C):
thuộc đường tròn (C): 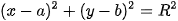 (tâm l(a;b), bán kính R). Khi đó, tiếp tuyến
(tâm l(a;b), bán kính R). Khi đó, tiếp tuyến 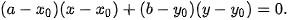







































































Bình Luận
Để Lại Bình Luận Của Bạn