Nội Dung Chính
(Trang 98)
| B Bất phương trình bậc hai một ẩn 22 Biến cố (là tập con của không gian mẫu) 78 Biến cố đối 79 Biến số 6 C Chỉnh hợp 67 Công thức tính khoảng cách từ một điểm đến một đường thẳng 40 Công thức tính góc giữa hai đường thẳng 38 Đ Định nghĩa cổ điển của xác suất 80 Đồ thị của hàm số 7 Đường chuẩn của parabol 52 Đường conic 48 E Elip 49 G Góc giữa hai đường thẳng 37 H Hàm số 6 Hàm số bậc hai 11 Hàm số bậc nhất trên từng khoảng 7 Hàm số cho bằng bảng 6 Hàm số cho bằng biểu đồ 6 Hàm số cho bằng công thức 6 Hàm số đồng biến 8 Hàm số nghịch biển 8 Hoán vị 66 Hypebol 50 N Nguyên lí xác suất bé 81 Nhị thức Newton 72 P Phương pháp tổ hợp 83 Phương trình chính tắc của elip 49 | Phương trình chính tắc của hypebol 51 Phương trình chính tắc của parabol 53 Phương trình đường tròn 43 Phương trình tham số của đường thẳng 34 Phương trình tổng quát của đường thẳng 32 Q Quy tắc cộng 61 Quy tắc nhân 63 S Sơ đồ hình cây 61 T Tam thức bậc hai 19 Tập giá trị (của hàm số) 6 Tập xác định (của hàm số) 6 Tham số tiêu của parabol 52 Tiêu điểm của parabol 52 Tiêu điểm, tiêu cự của elip 49 Tiêu điểm, tiêu cự của hypebol 50 Tính chất cơ bản của xác suất 80 Tính chất quang học của các đường conic 54 Tổ hợp 68 V Vectơ chỉ phương của đường thẳng 32 Vectơ pháp tuyến của đường thẳng 31 Vị trí tương đối giữa hai đường thẳng 36 X Xác suất của biến cố đối 85 |
(Trang 99)
| Thuật ngữ | Giải thích |
| Biến cố đối | Biến cố đối của biến cố E là biến cố xảy ra khi và chỉ khi E không xảy ra. |
| Định lí về dấu của tam thức bậc hai | Định lí cho phép xác định dấu của tam thức bậc hai 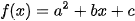  của nó. của nó. |
| Định nghĩa cổ điển của xác suất | Xác suất của biến cố E bằng tỉ số giữa số kết quả thuận lợi cho E và tổng số kết quả có thể. |
| Giải một phương trình | Tìm tất cả các nghiệm của nó (nghĩa là tìm tập hợp nghiệm). |
| Hai phương trình tương đương | Hai phương trình có cùng tập hợp nghiệm. |
| Nguyên lí xác suất bé | Nếu một biến cố có xác suất rất bé thì trong một phép thử biến cố đó sẽ không xảy ra. |
| Phép biến đổi tương đương một phương trình | Phép biến đổi phương trình đó thành một phương trình tương đương. |
| Phương pháp toạ độ trong mặt phẳng | Đưa vào mặt phẳng một hệ trục toạ độ và chuyển các đối tượng hình học sang đối tượng đại số tương ứng, từ đó dùng phương pháp và ngôn ngữ đại số để giải quyết các bài toán hình học. |
| Phương pháp tổ hợp | Sử dụng các quy tắc đếm, các công thức tính số hoán vị, chỉnh hợp và tổ hợp để tính số phần tử của không gian mẫu, của các biến cố. |
| Phương trình một ẩn x | Mệnh đề chứa biến có dạng f(x) = g(x), trong đó f(x) và g(x) là những biểu thức của x. |
| Xác suất của biến cố đối | Tổng xác suất của biến cố E với xác suất của biến cố đối bằng 1. |
| Xét chiều biến thiên của hàm số | Tìm các khoảng đồng biến và các khoảng nghịch biến của hàm số. |





































































Bình Luận
Để Lại Bình Luận Của Bạn