Nội Dung Chính
(Trang 66)
| THUẬT NGỮ • Hoán vị • Chỉnh hợp • Tổ hợp | KIẾN THỨC, KĨ NĂNG • Tính số hoán vị, chỉnh hợp, tổ hợp. • Tính số hoán vị, chỉnh hợp, tổ hợp bằng máy tính cầm tay. |
| Danh sách các cầu thủ của Đội tuyển bóng đá quốc gia tham dự một trận đấu quốc tế có 23 cầu thủ gồm 3 thủ môn, 7 hậu vệ, 8 tiền vệ và 5 tiền đạo. Huấn luyện viên rất bí mật, không cho ai biết đội hình (danh sách 11 cầu thủ) sẽ ra sân. Trong cuộc họp báo, ông chỉ tiết lộ đội sẽ đá theo sơ đồ 3–4–3 (nghĩa là 3 hậu vệ, 4 tiền vệ, 3 tiền đạo và 1 thủ môn). Đối thủ đã có danh sách 23 cầu thủ (tên và vị trí của từng cầu thủ) và rất muốn dự đoán đội hình, họ xét hết các khả năng có thể xảy ra. Hỏi nếu đối thủ đã dự đoán được trước vị trí thủ môn thì họ sẽ phải xét bao nhiêu đội hình có thể? | 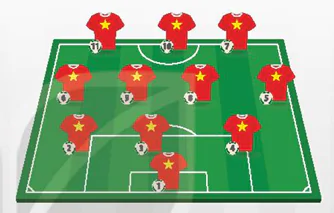 |
1. HOÁN VỊ
HĐ1. Một nhóm gồm bốn bạn Hà, Mai, Nam, Đạt xếp thành một hàng, từ trái sang phải, để tham gia một cuộc phỏng vấn.
|
Hà |
Mai |
Nam |
Đạt |
a) Hãy liệt kê ba cách sắp xếp bốn bạn trên theo thứ tự.
b) Có bao nhiêu cách sắp xếp thứ tự bốn bạn trên để tham gia phỏng vấn?
Nhận xét. Mỗi cách sắp xếp thứ tự của bốn bạn tham gia phỏng vấn ở HĐ1 được gọi là một hoán vị của tập hợp gồm bốn bạn này. Số các hoán vị của bốn bạn ở HĐ1 là 4 . 3 . 2 . 1.
(Trang 67)
Tổng quát ta có
| Một hoán vị của một tập hợp có n phần tử là một cách sắp xếp có thứ tự n phần tử đó (với n là một số tự nhiên, n ≥ 1). Số các hoán vị của tập hợp có n phần tử, kí hiệu là
|
Chú ý. Kí hiệu n.(n-1).(n-2) ... 2.1 là n! (đọc là n giai thừa), ta có: 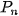 = n!. Chẳng hạn
= n!. Chẳng hạn 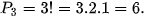
Quy ước 0! = 1.
Ví dụ 1. Từ các chữ số 6, 7, 8 và 9 có thể lập được bao nhiêu số có bốn chữ số khác nhau?
Giải
Mỗi cách sắp xếp bốn chữ số đã cho để lập thành một số có bốn chữ số khác nhau là một hoán vị của bốn chữ số đó.
Vậy số các số có bốn chữ số khác nhau có thể lập được là 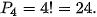
Luyện tập 1. Trong một cuộc thi điền kinh gồm 6 vận động viên chạy trên 6 đường chạy. Hỏi có bao nhiêu cách xếp các vận động viên vào các đường chạy đó?
2. CHỈNH HỢP
HĐ2. Trong lớp 10T có bốn bạn Tuấn, Hương, Việt, Dung đủ tiêu chuẩn tham gia cuộc thi hùng biện của trường.
a) Giáo viên cần chọn ra hai bạn phụ trách nhóm trên. Hỏi có bao nhiêu cách chọn hai bạn từ bốn bạn nêu trên?
b) Có bao nhiêu cách chọn hai bạn, trong đó một bạn làm nhóm trưởng, một bạn làm
nhóm phó?
Nhận xét. Trong HĐ2b, mỗi cách sắp xếp hai bạn từ bốn bạn làm nhóm trưởng, nhóm phó được gọi là một chỉnh hợp chập 2 của 4. Để tính số các chỉnh hợp ta dùng quy tắc nhân.
Tổng quát ta có:
| Một chỉnh hợp chập k của n là một cách sắp xếp có thứ tự k phần tử từ một tập hợp n phần tử (với k, n là các số tự nhiên, 1 ≤ k ≤ n ). Số các chỉnh hợp chập k của n, kí hiệu là
|
Ví dụ 2. Một lớp có 30 học sinh, giáo viên cần chọn lần lượt 4 học sinh trồng bốn cây khác nhau để tham gia lễ phát động Tết trồng cây của trường. Hỏi giáo viên có bao nhiêu cách chọn?
(Trang 68)
|
Mỗi cách chọn lần lượt 4 trong 30 học sinh để trồng bốn cây khác nhau là một chỉnh hợp chập 4 của 30. Vậy số cách chọn là Chú ý • Hoán vị sắp xếp tất cả các phần tử của tập hợp, còn chỉnh hợp chọn ra một số phần tử và sắp xếp chúng. • Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử đó. Vì vậy | Ngày 28-11-1959, Chủ tịch Hồ Chí Minh đã phát động ngày “Tết trồng cây với mong muốn: Trong mười năm, đất nước ta phong cảnh sẽ ngày càng tươi đẹp hơn, khí hậu điều hoà hơn, ...
|
Luyện tập 2. Trong một giải đua ngựa gồm 12 con ngựa, người ta chỉ quan tâm đến 3 con ngựa: con nhanh nhất, nhanh nhì và nhanh thứ ba. Hỏi có bao nhiêu kết quả có thể xảy ra?
3. TỔ HỢP
HĐ3. Trở lại HĐ2.
a) Hãy cho biết sự khác biệt khi chọn ra hai bạn ở câu HĐ2a và HĐ2b.
b) Từ kết quả tính được ở câu HĐ2b (áp dụng chỉnh hợp), hãy chỉ ra cách tính kết quả ở câu HĐ2a.
Nhận xét
Mỗi cách chọn ra 2 bạn từ 4 bạn ở HĐ2a được gọi là một tổ hợp chập 2 của 4. Vì không cần sắp xếp thứ tự hai bạn được chọn nên số cách chọn sẽ giảm đi 2! lần so với việc chọn ra hai bạn có sắp xếp thứ tự (ở câu HĐ2b).
Tổng quát ta có:
| Một tổ hợp chập k của n là một cách chọn k phần tử từ một tập hợp n phần tử (với k, n là các số tự nhiên, 0 ≤ k ≤n). Số các tổ hợp chập k của n, kí hiệu là
|
Chú ý
• 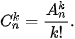
• Chỉnh hợp và tổ hợp có điểm giống nhau là đều chọn một số phần tử trong một tập hợp, nhưng khác nhau ở chỗ, chỉnh hợp là chọn có xếp thứ tự, còn tổ hợp là chọn không xếp thứ tự.
Ví dụ 3. Có 7 bạn học sinh muốn chơi cờ cá ngựa, nhưng mỗi ván chỉ có 4 người chơi. Hỏi có bao nhiêu cách chọn 4 bạn chơi cờ cá ngựa?
(Trang 69)
Giải
Mỗi cách chọn 4 bạn trong 7 bạn học sinh là một tổ hợp chập 4 của 7.
Vậy số cách chọn 4 bạn chơi cờ cá ngựa là 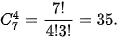
Luyện tập 3. Trong ngân hàng đề kiểm tra cuối học kì II môn Vật lí có 20 câu lí thuyết và 40 câu bài tập. Người ta chọn ra 2 câu lí thuyết và 3 câu bài tập trong ngân hàng đề để tạo thành một đề thi. Hỏi có bao nhiêu cách lập đề thi gồm 5 câu hỏi theo cách chọn như trên?
4. ỨNG DỤNG HOÁN VỊ, CHỈNH HỢP, TỔ HỢP VÀO CÁC BÀI TOÁN ĐẾM
Các khái niệm hoán vị, chỉnh hợp và tổ hợp liên quan mật thiết với nhau và là những khái niệm cốt lõi của các phép đếm. Rất nhiều bài toán đếm liên quan đến việc lựa chọn, việc sắp xếp, vì vậy các công thức tính 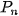 ,
, 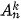 ,
, 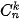 sẽ được dùng rất nhiều.
sẽ được dùng rất nhiều.
Dưới đây ta xét một số ví dụ về các bài toán đếm.
Ví dụ 4. Một lần anh Hưng đến Hà Nội và dự định từ Hà Nội tham quan Đền Hùng, Ninh Bình, Hạ Long, Đường Lâm và Bát Tràng, mỗi ngày đi tham quan một địa điểm rồi lại về Hà Nội.
a) Hỏi anh Hưng có thể xếp được bao nhiêu lịch trình đi tham quan tất cả các địa điểm (ở đây lịch trình tính cả thứ tự tham quan).
b) Anh Hưng có việc đột xuất phải về sớm, nên anh chỉ có 3 ngày để đi tham quan 3 địa điểm. Hỏi anh Hưng có bao nhiêu cách xếp lịch trình đi tham quan?
Giải
a) Anh Hưng đi tham quan 5 địa điểm, mỗi cách xếp lịch trình là một cách chọn có thứ tự của 5 địa điểm trên. Vậy số cách xếp lịch trình chính bằng số các hoán vị của 5 địa điểm, và bằng 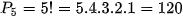 (cách).
(cách).
b) Nếu anh Hưng chỉ có 3 ngày để đi tham quan 3 nơi, thì mỗi cách xếp lịch trình của anh chính là một cách chọn có thứ tự 3 địa điểm từ 5 địa điểm, tức là một chỉnh hợp chập 3 của 5.
Vậy số cách xếp lịch trình đi tham quan trọng trường hợp này là 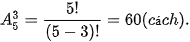
Ví dụ 5. Giải bài toán trong tình huống mở đầu về đội hình của Đội tuyển bóng đá quốc gia.
| Giải Vì mỗi đội hình gồm có 1 thủ môn, 3 hậu vệ, 4 tiền vệ và 3 tiền đạo và đã biết trước vị trí thủ môn, nên để chọn đội hình ta cần thực hiện 3 công đoạn: | 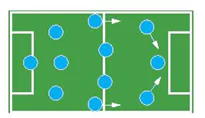 |
1. Chọn hậu vệ là chọn 3 trong số 7 hậu vệ: có 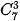 = 35 (cách).
= 35 (cách).
2. Chọn tiền vệ là chọn 4 trong số 8 tiền vệ: có 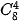 = 70 (cách).
= 70 (cách).
3. Chọn tiền đạo là chọn 3 trong số 5 tiền đạo: có 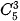 = 10 (cách).
= 10 (cách).
Vậy, theo quy tắc nhân, số các đội hình có thể có (khi đã biết vị trí thủ môn) là
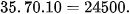
(Trang 70)
Vận dụng. Một câu lạc bộ có 20 học sinh.
a) Có bao nhiêu cách chọn 6 thành viên vào Ban quản lí ?
b) Có bao nhiêu cách chọn Trưởng ban, 1 Phó ban, 4 thành viên khác vào Ban quản lí?
5. SỬ DỤNG MÁY TÍNH CẦM TAY
Ta có thể dùng máy tính cầm tay để tính số các hoán vị, chỉnh hợp và tổ hợp.
Hoán vị
Để tính n!, ta ấn phím theo trình tự sau:
Ấn số n, ấn phím  , sau đó ấn phím
, sau đó ấn phím  . Khi đó, kết quả sẽ hiển thị ở dòng kết quả.
. Khi đó, kết quả sẽ hiển thị ở dòng kết quả.
| SHIFT | 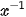 | = |
Ví dụ. Tính 9!.
Ta ấn liên tiếp các phím như sau: 
| 9 | SHIFT | 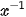 | = |
Dòng kết quả hiện ra 362 880.
Chỉnh hợp
Để tính 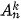 ta ấn phím theo trình tự sau:
ta ấn phím theo trình tự sau:
Ấn số n, ấn phím  , ấn số k, sau đó ấn phím
, ấn số k, sau đó ấn phím  . Khi đó, kết quả sẽ hiển thị ở dòng kết quả.
. Khi đó, kết quả sẽ hiển thị ở dòng kết quả.
| SHIFT | X | = |
Ví dụ. Tính 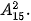
Ta ấn các phím theo trình tự sau: 
| 1 | 5 | SHIFT | X | 2 | = |
Dòng kết quả hiện ra 210.
Tổ hợp
Để tính 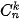 ta ấn phím theo trình tự sau:
ta ấn phím theo trình tự sau:
Ấn số n, ấn phím  , ấn số k, sau đó ấn phím
, ấn số k, sau đó ấn phím  . Khi đó, kết quả sẽ hiển thị ở dòng kết quả.
. Khi đó, kết quả sẽ hiển thị ở dòng kết quả.
| SHIFT | ÷ | = |
Ví dụ. Tính 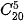
Ta ấn các phím theo trình tự sau: 
| 2 | 0 | SHIFT | ÷ | 5 | = |
Dòng kết quả hiện ra 15 504.
BÀI TẬP
8.6. Một hoạ sĩ cần trưng bày 10 bức tranh nghệ thuật khác nhau thành một hàng ngang. Hỏi có bao nhiêu cách để hoạ sĩ sắp xếp các bức tranh?
8.7. Từ các chữ số 0, 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên có ba chữ số khác nhau?
8.8. Có bao nhiêu cách chọn một tập hợp gồm hai số nguyên dương nhỏ hơn 100? Có bao nhiêu cách chọn một tập hợp gồm ba số nguyên dương nhỏ hơn 100?
8.9. Bạn Hà có 5 viên bi xanh và 7 viên bi đỏ. Có bao nhiêu cách để Hà chọn ra đúng 2 viên bi khác màu?
(Trang 71)
8.10. Một câu lạc bộ cờ vua có 10 bạn nam và 7 bạn nữ. Huấn luyện viên muốn chọn 4 bạn đi thi đấu cờ vua.
a) Có bao nhiêu cách chọn 4 bạn nam?
b) Có bao nhiêu cách chọn 4 bạn không phân biệt nam, nữ?
c) Có bao nhiêu cách chọn 4 bạn, trong đó có 2 bạn nam và 2 bạn nữ?
8.11. Có bao nhiêu số tự nhiên chia hết cho 5 mà mỗi số có bốn chữ số khác nhau?
| Em có biết?
• Câu hỏi một ván cờ vua có thể có nhiều nhất bao nhiêu nước đi có vẻ rất phức tạp vì mỗi ván một vẻ. Vậy mà bằng các tính toán tổ hợp, người ta đã chứng minh rằng về lí thuyết, một ván cờ có tối đa 5 950 nước đi. |




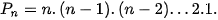
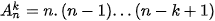 hay
hay 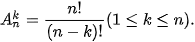
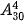 =657 720.
=657 720.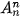

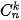 , được tính bằng công thức
, được tính bằng công thức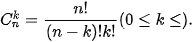
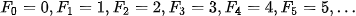 Trong dãy số này, kể từ số hạng thứ ba trở đi, mỗi số hạng bằng tổng của hai số hạng đứng ngay trước nó, tức là
Trong dãy số này, kể từ số hạng thứ ba trở đi, mỗi số hạng bằng tổng của hai số hạng đứng ngay trước nó, tức là 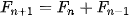 . Bằng các lập luận tổ hợp, có thể chứng minh được rằng tổng số các cách khác nhau để xếp được một hình chữ nhật có kích thước 1 × n từ hai loại gạch có kích thước 1 × 1 và 1 × 2 chính là
. Bằng các lập luận tổ hợp, có thể chứng minh được rằng tổng số các cách khác nhau để xếp được một hình chữ nhật có kích thước 1 × n từ hai loại gạch có kích thước 1 × 1 và 1 × 2 chính là 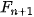 . Sử dụng tính chất này, ta có hằng đẳng thức
. Sử dụng tính chất này, ta có hằng đẳng thức 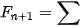 k+m=n
k+m=n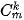
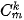 với k + m=n.
với k + m=n.





































































Bình Luận
Để Lại Bình Luận Của Bạn