Nội Dung Chính
| 1. Hiểu được các khái niệm về hình chiếu trục đo. 2. Biết cách vẽ hình chiếu trục đo của các vật thể đơn giản. |
I – KHÁI NIỆM
1. Thế nào là hình chiếu trục đo ?
Để dễ nhận biết hình dạng của vật thể, trên bản vẽ kĩ thuật thường dùng hình ba chiều như hình chiếu trục đo hoặc hình chiếu phối cảnh để bổ sung cho các hình chiếu vuông góc.
Hình chiếu trục đo được xây dựng như sau (hình 5.1):
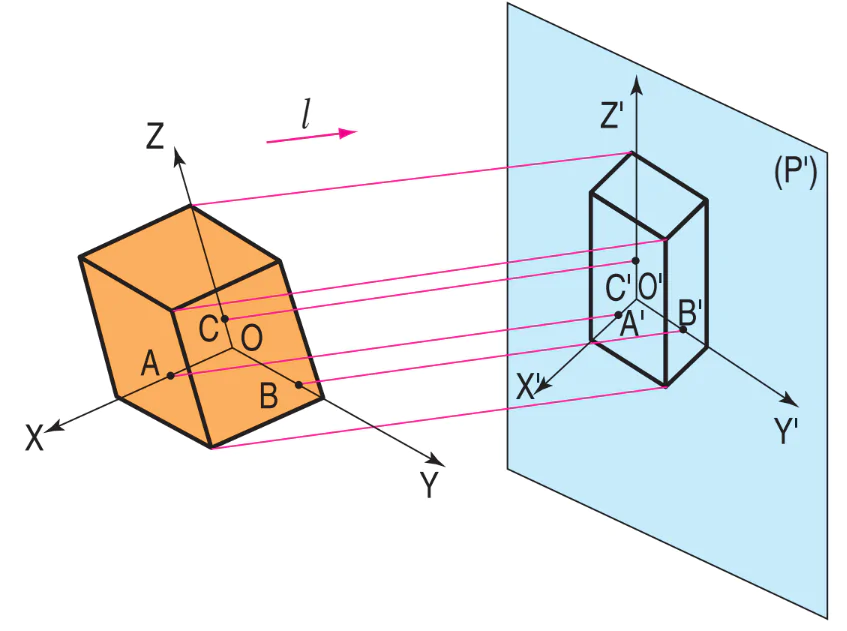
Hình 5.1. Phương pháp xây dựng hình chiếu trục đo
Giả sử một vật thể có gắn hệ toạ độ vuông góc OXYZ với các trục toạ độ đặt theo ba chiều dài, rộng và cao của vật thể. Chiếu vật thể cùng hệ toạ độ vuông góc lên mặt phẳng hình chiếu (P’) theo phương chiếu l (l không song song với (P’) và không song song với các trục toạ độ). Kết quả trên mặt phẳng (P’) nhận được một hình chiếu của vật thể và hệ toạ độ O’X’Y’Z. Hình biểu diễn đó gọi là hình chiếu trục đo của vật thể.
Vậy hình chiếu trục đo là hình biểu diễn ba chiều của vật thể được xây dựng bằng phép chiếu song song.
(?) Nếu phương chiếu l song song với mặt phẳng hình chiếu (P') hoặc song song với một trong ba trục toạ độ thì thế nào ?
2. Thông số cơ bản của hình chiếu trục đo
a) Góc trục đo
Trong phép chiếu trên, hình chiếu của các trục toạ độ là các trục O’X’, O’Y’ và O’Z’ gọi là trục đo. Góc giữa các trục đo : X’O’Y’, Y’O’Z và X’O’Z’ gọi là các góc trục đo.
b) Hệ số biến dạng
Hệ số biến dạng là tỉ số độ dài hình chiếu của một đoạn thẳng nằm trên trục toạ độ với độ dài thực của đoạn thẳng đó. Trên hình 5.1 có :
![]() là hệ số biến dạng theo trục O’X;
là hệ số biến dạng theo trục O’X;
![]() là hệ số biến dạng theo trục O’Y;
là hệ số biến dạng theo trục O’Y;
![]() là hệ số biến dạng theo trục O’Z.
là hệ số biến dạng theo trục O’Z.
Góc trục đo và hệ số biến dạng là hai thông số cơ bản của hình chiếu trục đo. Trên bản vẽ kĩ thuật thường dùng hai loại hình chiếu trục đo vuông góc đều và hình chiếu trục đo xiên góc cân.
(?) Các góc trục đo và các hệ số biến dạng thay đổi liên quan đến các yếu tố nào ?
II – HÌNH CHIẾU TRỤC ĐO VUÔNG GÓC ĐỀU
Trong hình chiếu trục đo vuông góc đều, phương chiếu vuông góc với mặt phẳng hình chiếu (l ⊥ (P')) và ba hệ số biến dạng bằng nhau (p = q = r).
1. Thông số cơ bản
a) Góc trục đo :
![]()
(hình 5.2).
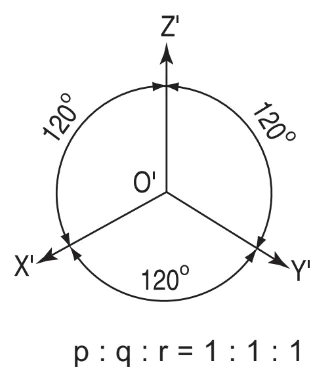
Hình 5.2. Góc trục đo (hình chiếu trục đo vuông góc đều)
b) Hệ số biến dạng : p = q = r
Để thuận tiện cho việc dựng hình, thường dùng hệ số biến dạng quy ước p = q = r = l và trục O’Z’ biểu thị chiều cao được đặt thẳng đứng.
2. Hình chiếu trục đo của hình tròn
Hình chiếu trục đo vuông góc đều của những hình tròn nằm trong các mặt phẳng song song với các mặt phẳng toạ độ là các hình elip có hướng khác nhau như hình 5.3. Nếu vẽ theo hệ số biến dạng quy ước (p = q = r = l) thì các elip đó có trục dài bằng 1,22d và trục ngắn bằng 0,71d (d là đường kính của hình tròn).
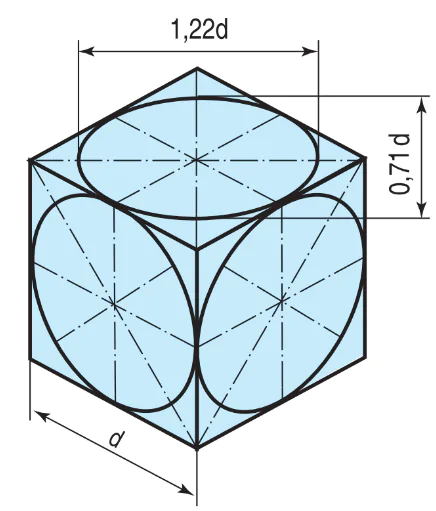
Hình 5.3. Hướng các elip
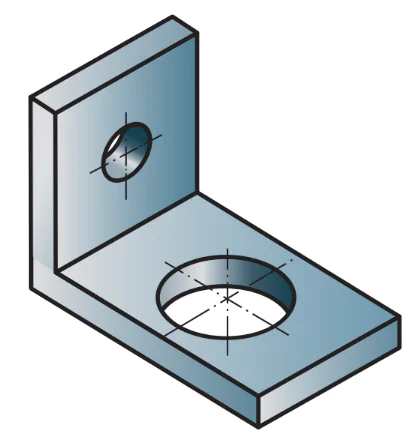
Hình 5.4. Hình chiếu trục đo vuông góc đều của chiếc ke góc
Hình 5.4 là hình chiếu trục đo vuông góc đều của chiếc ke góc. Hình chiếu trục đo vuông góc đều thường dùng để biểu diễn các vật thể có các hình khối tròn.
III – HÌNH CHIẾU TRỤC ĐO XIÊN GÓC CÂN
Trong hình chiếu trục đo xiên góc cân, phương chiếu không vuông góc với mặt phẳng hình chiếu, mặt phẳng toạ độ XOZ đặt song song với mặt phẳng hình chiếu (XOZ//(P’)). Có các thông số cơ bản như sau :
1. Góc trục đo :
![]()
(hình 5.5)
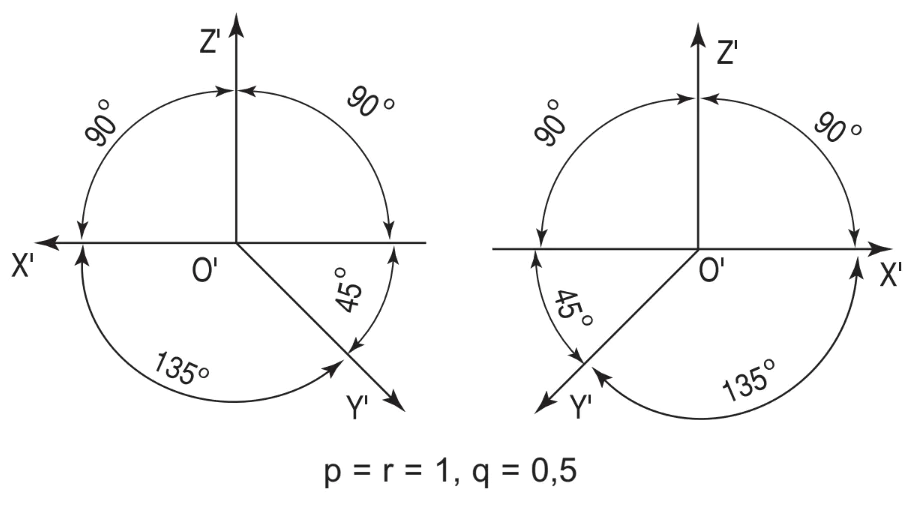
Hình 5.5. Góc trục đo (hình chiếu trục đo xiên góc cân)
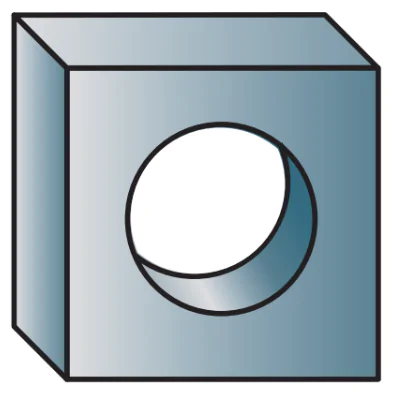
Hình 5.6. Hình chiếu trục đo xiên góc cân của tấm đệm
2. Hệ số biến dạng : p = r = l và q = 0,5.
Trong hình chiếu trục đo xiên góc cân, các mặt của vật thể song song với mặt phẳng toạ độ XOZ không bị biến dạng.
Hình 5.6 là hình chiếu trục đo xiên góc cân của tấm đệm.
(?) Tại sao trong hình chiếu trục đo xiên góc cân, các mặt của vật thể song song với mặt phẳng toạ độ XOZ không bị biến dạng ?
IV – CÁCH VẼ HÌNH CHIẾU TRỤC ĐO
Căn cứ vào đặc điểm hình dạng của vật thể để chọn cách vẽ hình chiếu trục đo thích hợp.
Khi vẽ, để thuận tiện cho việc dựng hình, thường đặt các trục toạ độ theo chiều dài, chiều rộng và chiều cao của vật thể, sau đó vẽ hình hộp ngoại tiếp theo các kích thước dài, rộng, cao của vật thể.
Bảng 5.1 trình bày cách vẽ hình chiếu trục đo xiên góc cân và hình chiếu trục đo vuông góc đều của vật thể có hình chiếu đứng và hình chiếu bằng cho trên hình 5.7.
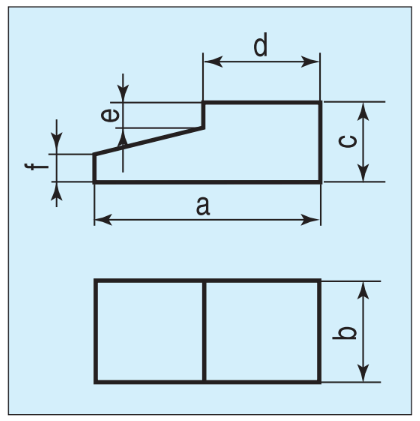
Hình 5.7. Các hình chiếu của vật thể
Bảng 5.1. Cách vẽ hình chiếu trục đo (HCTĐ) của vật thể
| Các bước vẽ | HCTĐ xiên góc cân (p = r = 1, q = 0,5) | HCTĐ vuông góc đều (p = q = r = 1) |
| a) Vẽ hình chiếu trục đo của hình hộp ngoại tiếp có kích thước : dài a, rộng b và cao c đặt lên ba trục đo theo các hệ số biến dạng của chúng. | 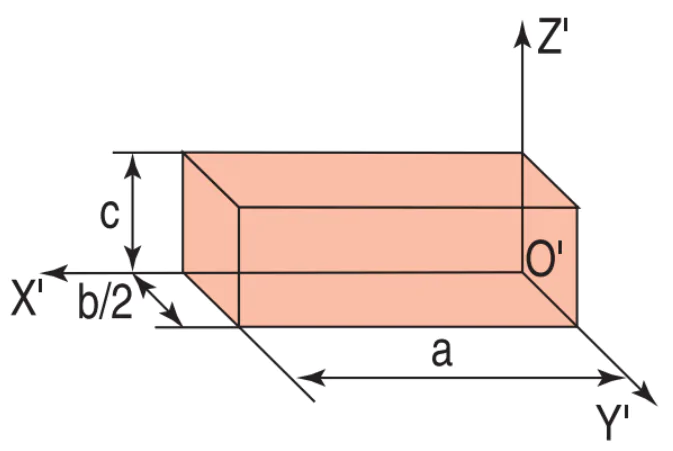 | 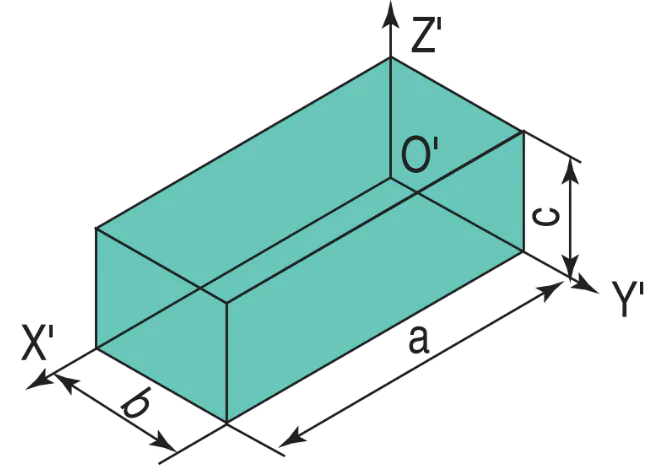 |
| b) Vẽ phần vát nghiêng bằng cách đặt chiều dài d của nó theo trục O’X' và chiều cao e và f theo trục O'Z' | 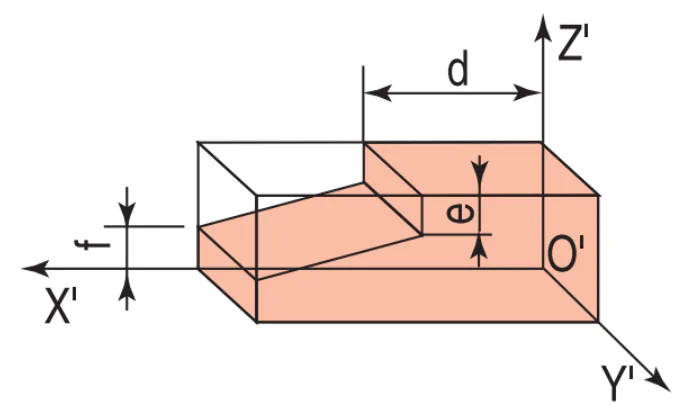 | 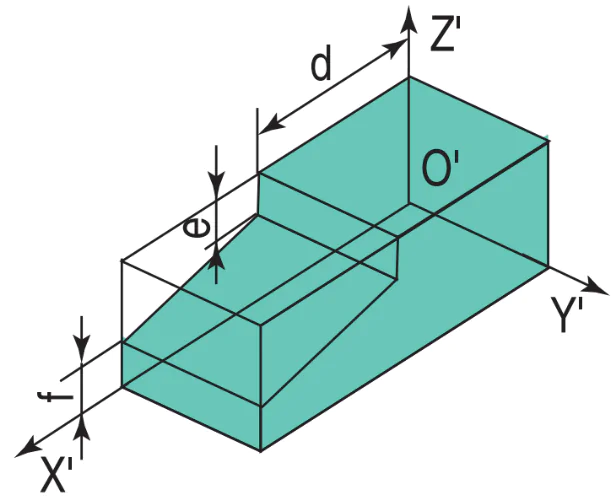 |
| c) Tẩy các đường nét phụ, tô đậm các cạnh thấy và hoàn thiện hình chiếu trục đo của vật thể | 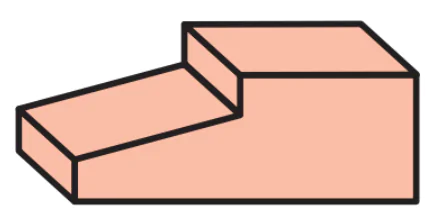 | 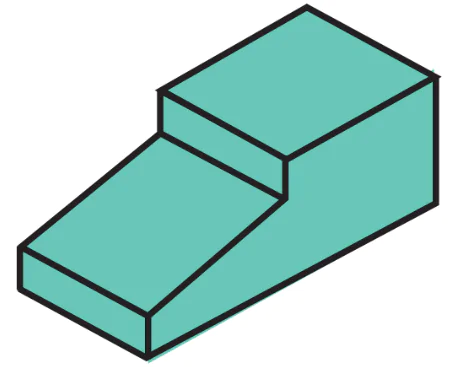 |
Câu hỏi
1. Trình bày cách xây dựng hình chiếu trục đo.
2. Thế nào là hệ số biến dạng ?
3. Trong hình chiếu trục đo vuông góc đều và hình chiếu trục đo xiên góc cân, các thông số cơ bản bằng bao nhiêu ?
4. Hình chiếu trục đo xiên góc cân có đặc điểm gì ?
Bài tập
1. Vẽ hình chiếu trục đo vuông góc đều của một hình nón cụt có đường kính đáy lớn bằng 40mm, đường kính đáy nhỏ bằng 30mm và chiều cao của hình nón cụt bằng 50mm.
2. Vẽ hình chiếu trục đo xiên góc cân của một hình chóp đều có đáy là một hình vuông, cạnh bằng 40mm và chiều cao của hình chóp bằng 50mm.
Thông tin bổ sung
1. Cách vẽ elip
Trong thực hành, thường dùng khuôn vẽ elip chuyên dùng cho loại hình chiếu trục đo vuông góc đều. Khuôn này là tấm phẳng (palét) có nhiều lỗ hình elip với các kích cỡ khác nhau (hình 5.8).

Hình 5.8. Khuôn vẽ elip
2. Cách vẽ gần đúng hình elip bằng compa
Trong vẽ kĩ thuật, cho phép dùng cách vẽ gần đúng hình elip bằng compa.
Ví dụ : Vẽ hình elip nằm trong mặt X’O’Y (hình 5.9). Cách vẽ như sau :
– Trước hết vẽ hình thoi ABCD có cạnh bằng d (d là đường kính của hình tròn), cạnh AB trùng với trục O’X’ và cạnh BC trùng với trục O'Y'.
– Nối đỉnh D với các điểm giữa E và F của cạnh hình thoi, DE và DF cắt đường chéo AC tại điểm O1, và O2.
– Vẽ các cung tròn có tâm là B, D với bán kính R1 = DE = DF = BH = BG và các cung tròn có tâm là O1, O2 với bán kính R2 = O2F = O1E ; các cung tròn này tạo thành hình elip gần đúng (hình 5.9).
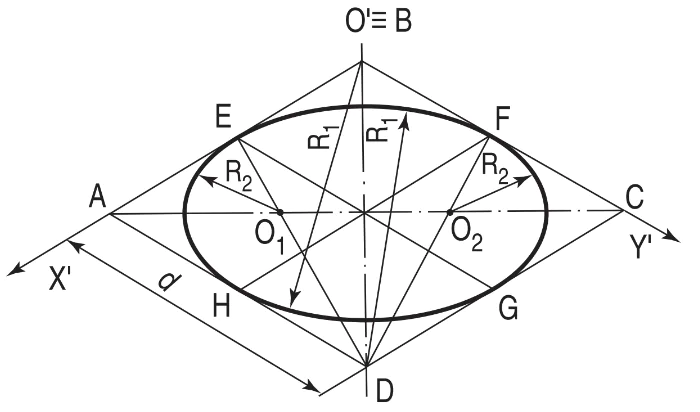
Hình 5.9. Cách vẽ gần đúng hình elip
















































Bình Luận
Để Lại Bình Luận Của Bạn