Nội Dung Chính
Chương II. SỐ THỰC
(SỐ HỌC)
Chúng ta đã biết mỗi đoạn thẳng đều có một độ dài, được biểu thị bởi một số. Trong chương này, chúng ta sẽ thấy có những đoạn thẳng mà độ dài của nó không thể biểu thị bằng một số hữu tỉ. Điều này cho thấy có một loại số mới, đó là số vô tỉ. Số vô tỉ và số hữu tỉ được gọi chung là số thực. Chúng ta cùng tìm hiểu về loại số này!

Bài 5. LÀM QUEN VỚI SỐ THẬP PHÂN VÔ HẠN TUẦN HOÀN
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| Số thập phân Số thập phân vô hạn tuần hoàn Chu kì Độ chính xác | • Nhận biết số thập phân hữu hạn và số thập phân vô hoàn. • Làm tròn số căn cứ vào độ chính xác cho trước |

Số thập phân vô hạn tuần hoàn
• Khi chia 5 cho 18, ta thấy phép chia không bao giờ chấm dứt và nếu cứ tiếp tục chia thì trong thương 0,2777..., chữ số 7 được lặp lại mãi. Ta nói phân số  viết được dưới dạng số thập phân là 0,2777.... Tương tự, ta có -
viết được dưới dạng số thập phân là 0,2777.... Tương tự, ta có -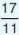 = - 1545454.... Các số 0,2777...; -1,545454... là những số thập phân vô hạn tuần hoàn.
= - 1545454.... Các số 0,2777...; -1,545454... là những số thập phân vô hạn tuần hoàn.
• Số 0,2777... được viết gọn là 0,2(7). Kí hiệu (7) được hiểu là chữ số 7 được lập lại vô hạn lần. Số 7 được gọi là chu kì của số thập phân vô hạn tuần hoàn 0,2(7). Tương tự, -1,545454... có chu kì là 54 và được viết gọn là -1.(54).
• Các số thập phân đã học như 0,8; 1,25; ... còn được gọi là số thập phân hữu hạn.
Kết quả của phép chia 1 cho 9 là số thập phân hữu hạn hay vô hạn tuần hoàn?
Ví dụ 1
Chu kì của số thập phân vô hạn tuần hoàn có thể có nhiều hơn một chữ số, chẳng hạn:
a) 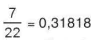 ... = 0,3(18) là số thập phân vô hạn tuần hoàn với chu kì là 18.
... = 0,3(18) là số thập phân vô hạn tuần hoàn với chu kì là 18.
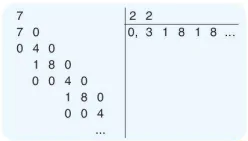
b) 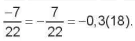
Luyện tập 1
Viết các phân số 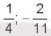 dưới dạng số thập phân rồi cho biết số nhận được là số thập phân hữu hạn hay vô hạn tuần hoàn.
dưới dạng số thập phân rồi cho biết số nhận được là số thập phân hữu hạn hay vô hạn tuần hoàn.
Chỉ ra chu kì rồi viết gọn nếu đó là số thập phân vô hạn tuần hoàn.
Chú ý
Mọi số hữu tỉ đều viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Làm tròn số thập phân căn cứ vào độ chính xác cho trước
Ở lớp 6, các em đã học cách làm tròn số thập phân hữu hạn đến một hàng nào đó. Ta cũng làm tròn số thập phân vô hạn theo cách tương tự. Chẳng hạn, nếu làm tròn a = 46,333... đến hàng đơn vị thì được kết quả là 46; nếu làm tròn b = -1,27(534) đến hàng phần trăm thì kết quả là - 1,28. Ta viết 46,333... ; -1,27(534)
; -1,27(534)  -1,28 (kí hiệu
-1,28 (kí hiệu 
Trên trục số Hình 2.1, ta thấy khoảng cách từ điểm 46 đến điểm a= 46,333... nhỏ hơn 0,5 (bằng một nửa khoảng cách từ điểm 46 đến điểm 47). Ta cũng nói rằng 46 là kết quả làm tròn của a = 46,333... với độ chính xác 0,5.
Tổng quát, ta có:
Khi làm tròn số một hàng nào đó, kết quả làm tròn có đọ chính xác bằng một nửa đơn vị hàng làm tròn.
Chú ý. Muốn làm tròn số thập phân với độ chính xác cho trước, ta có thể xác định hàng làm tròn thích hợp bằng cách sử dụng bảng bên.
| Hàng làm tròn | Độ chính xác |
| trăm | 50 |
| chục | 5 |
| đơn vị | 0,5 |
| phần mười | 0,05 |
| phần trăm | 0,005 |
Ví dụ 2 Làm tròn số 12 591,27 với độ chính xác:
a) 50;
b) 0,05.
Giải
a) Để kết quả làm tròn có độ chính xác là 50, ta làm tròn số đến hàng trăm.
Áp dụng quy tắc làm tròn số ta được 12 591,27 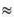 12 600.
12 600.
b) Để kết quả làm tròn có độ chính xác là 0,05, ta làm tròn số đến hàng phần mười, được kết quả là: 12 591,27 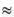 12 591,3.
12 591,3.
Luyện tập 2 Làm tròn số 3,14159 với độ chính xác 0,005.
Vận dụng
Ước lượng kết quả phép tính 31, (81) . 4,9 bằng cách làm tròn hai thửa số đến hàng đơn vị.
BÀI TẬP
2.1. Trong các số thập phân sau, số nào là số thập phân hữu hạn? Số nào là số thập phân vô hạn tuần hoàn?
0,1; -1,(23); 11,2(3); -6.725.
2.2. Sử dụng chu kì, hãy viết gọn số thập phân vô hạn tuần hoàn 0,010101...
2.3. Tìm chữ số thập phân thứ năm của số 3,2(31) và làm tròn số 3,2(31) đến chữ số thập phân thứ năm.
2.4. Só 0,1010010001000010... (viết liên tiếp các số 10, 100, 1000, 10 000,... sau dấu phẩy) có phải là số thập phân vô hạn tuần hoàn hay không?
2.5. Làm tròn số 3,14159...
a) đến chữ số thập phân thứ ba;
b) với độ chính xác 0,005.
EM CÓ BIẾT?
Người ta đã chứng minh được rằng:
Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn. Chẳng hạn:

Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thị phân số đó viết được dưới dạng số thập 2 phân vô hạn tuần hoàn. Chẳng hạn:

Mỗi số thập phân vô hạn tuần hoàn biểu diễn một số hữu tỉ.
Chẳng hạn: 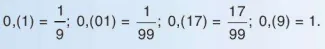







































Bình Luận
Để Lại Bình Luận Của Bạn