Trang 48
| THUẬT NGỮ • Cấp số cộng • Công sai • Số hạng tổng quát • Tổng của n số hạng đầu | KIẾN THỨC, KĨ NĂNG • Nhận biết một dãy số là cấp số cộng. • Giải thích công thức xác định số hạng tổng quát của cấp số cộng. • Tính tổng của n số hạng đầu của cấp số cộng. • Giải quyết một số vấn đề thực tiễn gắn với cấp số cộng. |

Một nhà hát có 25 hàng ghế với 16 ghế ở hàng thử nhất, 18 ghế ở hàng thứ hai, 20 ghế ở hãng thứ ba và cứ tiếp tục theo quy luật đó, tức là hàng sau nhiều hơn hàng liền trước nó 2 ghế. Tinh tổng số ghế của nhà hát đó.
1. ĐỊNH NGHĨA
HĐ1. Nhận biết cấp số cộng
Cho dãy số ( ) gồm tất cả các số tự nhiên lẻ, xếp theo thứ tự tăng dần.
) gồm tất cả các số tự nhiên lẻ, xếp theo thứ tự tăng dần.
a) Viết năm số hạng đầu của dãy số.
b) Dự đoán công thức biểu diễn số hạng  theo số hạng
theo số hạng 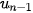
| • Cấp số cộng là một dãy số (hữu hạn hay vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d. Số d được gọi là công sai của cấp số cộng. • Cấp số cộng (  ) với công sai d được cho bởi hệ thức truy hồi ) với công sai d được cho bởi hệ thức truy hồi 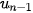 với n ≥2. với n ≥2. |
 Dãy số không đổi a, a, a, ... có phải là một cấp số cộng không?
Dãy số không đổi a, a, a, ... có phải là một cấp số cộng không?
Ví dụ 1. Cho cấp số cộng ( ) có số hạng đầu
) có số hạng đầu  = 2 và công sai d = 3. Hãy viết năm số hạng đầu của cấp số cộng này.
= 2 và công sai d = 3. Hãy viết năm số hạng đầu của cấp số cộng này.
Giải
Năm số hạng đầu của cấp số cộng này là

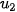 =
=  + d = 2 + 3 = 5,
+ d = 2 + 3 = 5, 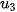 =
= 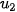 + d = 5 + 3 = 8,
+ d = 5 + 3 = 8, 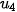
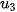 + d = 8 + 3 = 11,
+ d = 8 + 3 = 11, 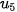 =
= 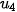 + d = 11 + 3 = 14.
+ d = 11 + 3 = 14. Trang 49
Ví dụ 2. Cho dãy số ( ) với
) với 
 ) là một cấp số cộng. Tìm số hạng đầu
) là một cấp số cộng. Tìm số hạng đầu 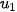 và công sai d của nó.
và công sai d của nó. Giải
Ta có,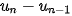 = (5n − 1) – [5(n - 1) – 1] = 5, với mọi n ≥ 2.
= (5n − 1) – [5(n - 1) – 1] = 5, với mọi n ≥ 2.
Do đó ( ) là cấp số cộng có số hạng đầu
) là cấp số cộng có số hạng đầu 

Để chứng minh ( ) là một cấp số cộng, hãy chứng minh hiệu hai số hạng liên tiếp
) là một cấp số cộng, hãy chứng minh hiệu hai số hạng liên tiếp 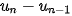 không đổi.
không đổi.
Luyện tập 1. Cho dãy số ( ) với
) với 
 ) là một cấp số cộng. Xác định số hạng đầu và công sai của cấp số cộng này.
) là một cấp số cộng. Xác định số hạng đầu và công sai của cấp số cộng này. 2. SỐ HẠNG TỔNG QUÁT
HĐ2. Công thức số hạng tổng quát của cấp số cộng
Cho cấp số cộng ( ) với số hạng đầu
) với số hạng đầu  và công sai d.
và công sai d.
a) Tính các số hạng 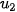 ,
, 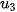
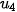 ,
, 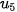 theo
theo  và d.
và d. b) Dự đoán công thức tính số hạng tổng quát  theo
theo 
Nếu cấp số cộng ( ) có số hạng đầu ) có số hạng đầu  và công sai d thì số hạng tổng quát và công sai d thì số hạng tổng quát  của nó được xác định theo công thức của nó được xác định theo công thức = =  |
Ví dụ 3. Tìm năm số hạng đầu và số hạng thứ 100 của cấp số cộng ( ): 10, 5, ...
): 10, 5, ...
Giải
Cấp số cộng này có số hạng đầu  = 10 và công sai d = –5.
= 10 và công sai d = –5.
Do đó năm số hạng đầu là: 10, 5, 0, -5, -10.
Số hạng thứ 100 là 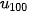 =
=  + (100 – 1)d = 10 + 99 · (-5) = 485.
+ (100 – 1)d = 10 + 99 · (-5) = 485.
Ví dụ 4. Số hạng thứ 10 của một cấp số cộng (
Giải
Giả sử  là số hạng đầu và d là công sai của cấp số cộng đó. Ta có:
là số hạng đầu và d là công sai của cấp số cộng đó. Ta có:
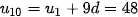
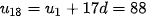
Giải hệ này ta được  = 3 và d = 5.
= 3 và d = 5.
Vậy số hạng thứ 100 của cấp số cộng này là 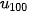
 + 99d = 3 + 99 · 5 = 498.
+ 99d = 3 + 99 · 5 = 498. Luyện tập 2. Cho dãy số ( ) với
) với  = 4n – 3. Chứng minh rằng (
= 4n – 3. Chứng minh rằng ( ) là một cấp số cộng. Xác định số hạng đầu
) là một cấp số cộng. Xác định số hạng đầu 
 dưới dạng
dưới dạng  =
=  + (n - 1)d.
+ (n - 1)d. Trang 50
3.TỔNG n SỐ HẠNG ĐẦU CỦA MỘT CẤP SỐ CỘNG
HĐ3. Xây dựng công thức tính tổng n số hạng đầu của cấp số cộng
Cho cấp số cộng ( ) với số hạng đầu
) với số hạng đầu 
Để tính tổng của n số hạng đầu
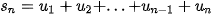 ,
,
hãy lần lượt thực hiện các yêu cầu sau:
a) Biểu diễn mỗi số hạng trong tổng S, theo số hạng đầu u, và công sai d.
b) Viết 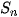 theo thứ tự ngược lại:
theo thứ tự ngược lại: 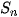 =
=  +
+ 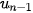
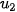 +
+  và sử dụng kết quả ở phần a) đề biểu diễn mỗi số hạng trong tổng này theo
và sử dụng kết quả ở phần a) đề biểu diễn mỗi số hạng trong tổng này theo  và d.
và d. c) Cộng từng vế hai đằng thức nhận được ở a), b), để tính 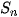 theo
theo 
Cho cấp số cộng ( ) với công sai d. Đặt ) với công sai d. Đặt 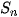 = =  + + 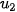 + ... + + ... +  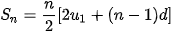 |
Chú ý. Sử dụng công thức  =
=  + (n −1)d, ta có thể viết tổng
+ (n −1)d, ta có thể viết tổng 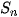 dưới dạng
dưới dạng
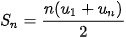 |
Ví dụ 5. Giải bài toán ở tình huống mở đầu.
Giải. Số ghế ở mỗi hàng của nhà hát lập thành một cấp số cộng, gồm 25 số hạng, với số hạng đầu  = 16 và công sai d = 2. Tổng các số hạng này là
= 16 và công sai d = 2. Tổng các số hạng này là
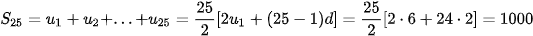 .
.
Vậy nhà hát đó có tổng cộng 1.000 ghế.
Ví dụ 6. Cần lấy tổng của bao nhiêu số hạng đầu của cấp số cộng 2, 5, 8, ... đề được kết quả bằng 345?
Giải
Cấp số cộng này có số hạng đầu  = 2 và công sai d = 3. Gọi n là số các số hạng đầu của cấp số cộng cần lấy tổng, ta có
= 2 và công sai d = 3. Gọi n là số các số hạng đầu của cấp số cộng cần lấy tổng, ta có
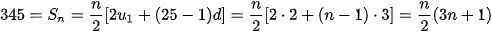 .
.
Do đó 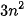
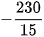 (loại) và n = 15.
(loại) và n = 15. Vậy phải lấy tổng của 15 số hạng đầu của cấp số cộng đã cho để được tổng bằng 345.
Vận dụng. Anh Nam được nhận vào làm việc ở một công ty về công nghệ với mức lương khởi điểm là 100 triệu đồng một năm. Công ty sẽ tăng thêm lương cho anh Nam mỗi năm là 20 triệu đồng. Tinh tổng số tiền lương mà anh Nam nhận được sau 10 năm làm việc cho công ty đó.
Trang 51
| Góc công nghệ  được kí hiệu ngắn gọn như sau: được kí hiệu ngắn gọn như sau: 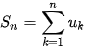 (kí hiệu Σ đọc là xích ma). (kí hiệu Σ đọc là xích ma).Ta có thể sử dụng máy tính cầm tay để tính tổng n số hạng liên tiếp của một dãy số khi biết công thức của số hạng tổng quát. Chẳng hạn, cho dãy số (  ) có số hạng tổng quát là ) có số hạng tổng quát là  = 3n + 1. Để tính tổng 35 số hạng đầu của dãy số đó, ta có thể dùng máy tính cầm tay, nhấn lần lượt các phim: SHIFT → x, = 3n + 1. Để tính tổng 35 số hạng đầu của dãy số đó, ta có thể dùng máy tính cầm tay, nhấn lần lượt các phim: SHIFT → x,   Tiếp theo ta nhập công thức số hạng tổng quát vào trong ngoặc (), rồi nhấn ↓ để nhập giá trị đầu tiên của x (ở đây là 1), sau đó nhấn ↑ để nhập giá trị cuối cùng của x (trường hợp này là 35), cuối cùng nhấn phím  . Khi đó, màn hình sẽ hiển thị kết quả cần tính như hình bên. . Khi đó, màn hình sẽ hiển thị kết quả cần tính như hình bên.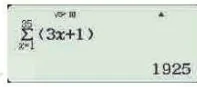 |
BÀI TẬP
2.8. Xác định công sai, số hạng thứ 5, số hạng tổng quát và số hạng thứ 100 của mỗi cấp số cộng sau:
a) 4, 9, 14, 19, ...;
b) 1, -1, -3, -5, ...;
2.9. Viết năm số hạng đầu của mỗi dãy số ( ) sau và xét xem nó có phải là cấp số cộng không. Nếu dãy số đó là cấp số cộng, hãy tìm công sai d và viết số hạng tổng quát của
) sau và xét xem nó có phải là cấp số cộng không. Nếu dãy số đó là cấp số cộng, hãy tìm công sai d và viết số hạng tổng quát của
nó dưới dạng 
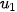 +(n - 1).
+(n - 1). a)  = 3 + 5n;
= 3 + 5n;
b)  = 6n - 4;
= 6n - 4;
c) 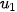 = 2,
= 2, 
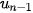 + n;
+ n; d) 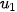 = 2,
= 2,  =
= 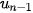 + 3.
+ 3.
2.10. Một cấp số cộng có số hạng thứ 5 bằng 18 và số hạng thứ 12 bằng 32. Tìm số hạng thứ 50 của cấp số cộng này.
2.11. Một cấp số cộng có số hạng đầu bằng 5 và công sai bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số cộng này để có tổng bằng 2 700?
2.12. Giả của một chiếc xe ô tô lúc mới mua là 680 triệu đồng. Cứ sau mỗi năm sử dụng, giá của chiếc xe ô tô giảm 55 triệu đồng. Tính giá còn lại của chiếc xe sau 5 năm sử dụng.
2.13. Một kiến trúc sư thiết kế một hội trưởng với 15 ghế ngồi ở hàng thứ nhất, 18 ghế ngồi ở hàng thứ hai, 21 ghế ngồi ở hàng thứ ba, và cứ như vậy (số ghế ở hàng sau nhiều hơn 3 ghế so với số ghế ở hãng liền trước nó). Nếu muốn hội trưởng đó có sức chứa ít nhất 870 ghế ngồi thì kiến trúc sư đó phải thiết kế tối thiểu bao nhiêu hàng ghế?
2.14. Vào năm 2020, dân số của một thành phố là khoảng 1,2 triệu người. Giả sử mỗi năm, dân số của thành phố này tăng thêm khoảng 30 nghìn người. Hãy ước tính dân số của thành phố này vào năm 2030.
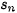 =
= 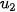











































































Bình Luận
Để Lại Bình Luận Của Bạn