Trang 78
| THUẬT NGỮ • Hai đường thẳng đồng phẳng • Hai đường thẳng chéo nhau | KIẾN THỨC, KĨ NĂNG • Nhận biết vị trí tương đối của hai đường thằng trong không gian: hai đường thẳng trùng nhau, song song, cắt nhau, chéo nhau. • Giải thích tính chất cơ bản của hai đường thẳng song song trong không gian. • Vận dụng kiến thức về hai đường thẳng song song để mô tả một số hình ảnh trong thực tiễn. |
Để giải quyết vấn đề tắc đường ở các thành phố lớn, có rất nhiều giải pháp được đưa ra. Trong đó giải pháp xây dựng các hệ thống cầu vượt, đường hoặc đường sắt trên cao đã và đang được đưa vào thực tế ở Việt Nam. Toán học mô tả vị trí tương quan giữa các tuyến đường trên như thế nào?

Hình 4.13
1. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG
HĐ1. Quan sát bốn tuyến đường trong Hình 4.13 và trả lời các câu hỏi sau:
a) Hai tuyến đường nào giao nhau?
b) Hai tuyến đường nào không giao nhau?
c) Hai tuyến đường nào song song?
| Cho hai đường thẳng a và b trong không gian. • Nếu a và b cùng nằm trong một mặt phẳng thì ta nói a và b đồng phẳng. Khi đó, a và b có thể cắt nhau, song song với nhau hoặc trùng nhau. Nếu a và b không cùng nằm trong bất kì mặt phẳng nào thì ta nói a và b chéo nhau. Khi đó, ta cũng nói a chéo với b, hoặc b chéo với a. |

a ∩ b = {M}, a cắt b tại M
a // b, a song song với b
a = b, a trùng với b
Hình 4.14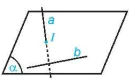
Hình 4.15
Trang 79
 Hãy tìm một số hình ảnh về hai đường thẳng song song, hai đường thẳng chéo nhau trong thực tiễn.
Hãy tìm một số hình ảnh về hai đường thẳng song song, hai đường thẳng chéo nhau trong thực tiễn.

Dệt vải bằng khung cửi, một trong những nét đẹp văn hoá của một số dân tộc.

Hành lang với bộ cảm biến an ninh gồm các tia laze đôi một không cắt nhau.
Nhận xét
– Hai đường thẳng song song là hai đường thẳng đồng phẳng và không có điểm chung.
– Có đúng một mặt phẳng chứa hai đường thẳng song song.

Hai đường thẳng không có điểm chung thì có thể song song hoặc chéo nhau.
Ví dụ 1. Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng (H.4.16).
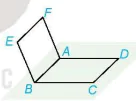
a) Quan sát bốn đường thẳng AB, BC, CD, DA. Chỉ ra các cặp đường thẳng cắt nhau, các cặp đường thẳng song song.
b) Trong ba đường thẳng AB, AF, BE có hai đường thẳng nào chéo nhau hay không?
Giải
a) Các cặp đường thẳng cắt nhau là AB và BC, AB và DA, BC và CD, CD và DA.
Các cặp đường thẳng song song là AB và CD, DA và BC.
b) Các đường thẳng AB, AF, BE cùng nằm trong mặt phẳng (ABEF) nên trong ba đường thẳng đó không có hai đường thẳng nào chéo nhau.
Luyện tập 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.17).
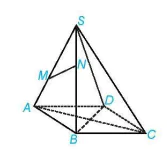
Hình 4.17
a) Trong các đường thẳng AB, AC, CD, hai đường thẳng nào song song, hai đường thẳng nào cắt nhau?
b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh SA, SB. Trong các đường thẳng SA, MN, AB có hai đường thằng nào chéo nhau hay không?
Trang 80
Ví dụ 2. Cho hình tứ diện ABCD (H.4.18). Hai đường thằng AB và CD có chéo nhau hay không? Chỉ ra các cặp đường thẳng chéo nhau có trong hình tứ diện đó.
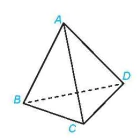
Hình 4.18
Giải
Nếu hai đường thẳng AB và CD không chéo nhau thì chúng cùng thuộc một mặt phẳng. Khi đó bốn điểm A, B, C, D đồng phẳng, trái với giả thiết ABCD là hình tứ diện. Do đó, hai đường thẳng AB và CD chéo nhau.
Lập luận tương tự, ta thấy trong tứ diện ABCD còn có các cặp đường thẳng chéo nhau là AC và BD, AD và BC.
Luyện tập 2. Trong hình chóp tứ giác S.ABCD (H.4.19), chỉ ra những đường thẳng:
a) Chéo với đường thẳng SA;
b) Chéo với đường thẳng BC.
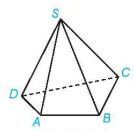
Hình 4.19
Vận dụng 1. Một chiếc gậy được đặt một đầu dựa vào tưởng và đầu kia trên mặt sàn (H.4.20). Hỏi có thể đặt chiếc gậy đó song song với một trong các mép tường hay không?

Hình 4.20
2. TÍNH CHẤT CỦA HAI ĐƯỜNG THẲNG SONG SONG
HĐ2. Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là một phẳng chứa M và d.
a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d.
b) Nếu một đường thằng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?
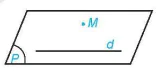
Hình 4.21
| Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho. |
HĐ3. Quan sát lớp học và tìm hai đường thẳng song song với mép trên của bảng. Hai đường thẳng đó có song song với nhau hay không?
| Trong không gian, hai đường thẳng phân biệt cũng song song với đường thẳng thứ ba thì song song với nhau. |

Các tia sáng Mặt Trời ở gần Trái Đất được coi như các đường thẳng đôi một song song với nhau.
Trang 81
Ví dụ 3. Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các đoạn thẳng AB, CD, AD, BC, AC, BD (H.4.22).
a) Chứng minh rằng tứ giác MPNQ là hình binh hành.
b) Chứng minh rằng các đoạn thẳng MN, PQ, RS cùng đi qua trung điểm của mỗi đoạn.
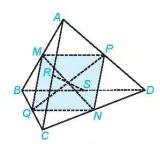
Hình 4.22
Giải
a) Trong tam giác ABC, ta có MQ là đường trung bình nên MQ // AC và MQ = 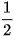
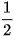 AC. Do đó MQ // PN và MQ = PN,
AC. Do đó MQ // PN và MQ = PN,
suy ra tứ giác MPNQ là hình bình hành.
b) Từ câu a suy ra hai đoạn thẳng MN và PQ cắt nhau tại trung điểm của mỗi đoạn. Tương tự, hai đoạn thẳng MN và RS cắt nhau tại trung điểm của mỗi đoạn. Do đó, các đoạn thẳng MN, PQ, RS cùng đi qua trung điểm của mỗi đoạn.

Nêu các dấu hiệu nhận biết tứ giác là hình bình hành.
Luyện tập 3. Trong Ví dụ 1, chứng minh rằng bốn điểm C, D, E, F đồng phẳng và tứ giác CDFE là hình bình hành.
HĐ4. Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Một mặt phẳng (R) cắt (P) và (Q) lần lượt theo các giao tuyến a và b khác c.
a) Nếu hai đường thẳng a và c cắt nhau tại M thì đường thẳng b có đi qua M hay không (H.4.23)? Giải thích vì sao.
b) Nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c có song song với nhau hay không (H.4.24)? Giải thích vì sao.
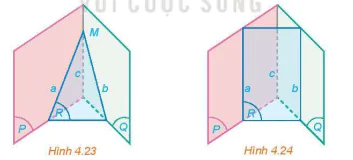
Hình 4.23
Hình 4.24
Kết quả sau đây còn được biết đến với tên gọi "Định lí về ba đường giao tuyến".

Nếu hai đường thẳng b và c cắt nhau tại N thì ta có thể sử dụng lại kết quả ở câu a.
| Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó đồng quy hoặc đối một song song với nhau. |
Chú ý. Từ kết quả trên có thể suy ra rằng: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đỗ hoặc trùng với một trong hai đường thẳng đó.
Trang 82
Ví dụ 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.25). Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).
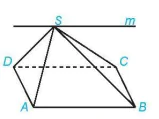
Hình 4.25
Giải
Hai mặt phẳng (SAB) và (SCD) có điểm chung S và chứa hai đường thẳng song song là AB và CD. Do đó, giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng m đi qua S và song song với AB, CD.
Luyện tập 4. Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).
Vận dụng 2. Một bể kính chứa nước có đáy là hình chữ nhật được đặt nghiêng như Hình 4.26. Giải thích tại sao đường mép nước AB song song với cạnh CD của bề nước.

Hình 4.26
BÀI TẬP
4.9. Trong không gian, cho ba đường thẳng a, b, c. Những mệnh đề nào sau đây là đúng?
a) Nếu a và b không cắt nhau thì a và b song song.
b) Nếu b và c chéo nhau thì b và c không cùng thuộc một mặt phẳng.
c) Nếu a và b cùng song song với c thì a song song với b.
d) Nếu a và b cắt nhau, b và c cắt nhau thì a và c cắt nhau.
4.10. Cho hình chóp S.ABCD có đáy là hình bình hành. Trong các cặp đường thẳng sau, cặp đường thẳng nào cắt nhau, cặp đường thằng nào song song, cặp đường thẳng nào chéo nhau?
a) AB và CD,
b) AC và BD,
c) SB và CD.
4.11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình
bình hành.
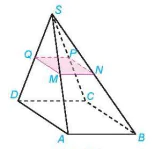
Hình 4.27
4.12. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng tứ giác MNCD là hình thang.
4.13. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28).
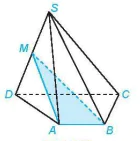
Hình 4.28
a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD).
b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD.
Trang 83
4.14. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC. Xác định giao tuyến của hai mặt phẳng (AMN) và (BPD) và chứng minh giao tuyến đó song song với BD.
4.15. (Đố vui) Khi hai cánh cửa sổ hình chữ nhật được mở, dù ở vị trí nào, thì hai mép ngoài của chúng luôn song song với nhau (H.4.29). Hãy giải thích tại sao.
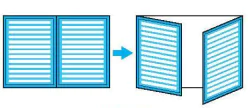
Hình 4.29
Nếu hai cánh cửa sổ có dạng hình thang như Hình 4.30 thì có vị trí nào của hai cánh cửa đề hai mép ngoài của chúng song song với nhau hay không?
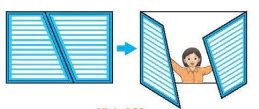
Hình 4.30
Em có biết?
Trong không gian, cố định một đường thẳng Δ thẳng đứng và gọi d là một đường thẳng tuỳ ý. Ta hãy cùng tìm hiểu hình được tạo bởi đường thẳng d khi quay đường thẳng này quanh đường thẳng Δ trong không gian. Nếu d song song với Δ hoặc d cắt Δ thì có thể dễ dàng hình dung được hình tạo ra là mặt trụ hoặc mặt nón (H.4.31).
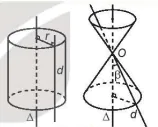
Còn nếu d và Δ chéo nhau thì sao? Trong hầu hết các trường hợp, hình tạo ra được gọi là mặt hypebol (hyperboloid) như trong Hình 4.32. Mặt hypebol có thể được coi như một "dạng 3D" của đường hypebol đã được dạy ở lớp 10. Một điều thú vị là nếu mặt hypebol được cắt bởi một mặt phẳng đi qua đường thẳng Δ (trục hypebol) thì vết cắt nhận được chính là một đường hypebol (H.4.33).
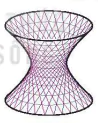
Hình 4.32
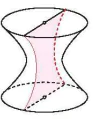
Hình 43.3
Hình ảnh của mặt hypebol xuất hiện rất nhiều trong xây dựng, kiến trúc, nghệ thuật,... và trong thực tiễn, chứng ta hoàn toàn có thể “dựng được" mặt hypebol bằng cách sử dụng các vật dụng đơn giản như nan tre thẳng, que tính hay những chiếc đũa,... Em có thể tìm thấy một cách dựng như vậy trên các trang web tìm kiếm với từ khóa "hyperboloid".












































































Bình Luận
Để Lại Bình Luận Của Bạn