Nội Dung Chính
Trang 70
Ở các lớp dưới, ta đã học về Hình học phẳng, môn học nghiên cứu tính chất của các hình trong mặt phẳng như hình tam giác, hình tứ giác, hình tròn... Tuy nhiên, các vật thể thường gặp trong thực tế đời sống như hộp phấn, cục tẩy, chặn giấy là các hình trong không gian. Một số tính chất của những hình này đã được giới thiệu và thừa nhận trong phần Hình học trực quan. Trong chương này, ta sẽ tiếp tục học về Hình học không gian, môn học nghiên cứu tinh chất của các hình trong không gian dựa trên các lập luận toán học logic và chặt chẽ. Nội dung chính của chương liên quan đến đường thẳng, mặt phẳng trong không gian và vị trí tương đối giữa chúng.

Hình học không gian đóng vai trò quan trọng trong xây dựng và đồ hoạ như vẽ kĩ thuật, in 3D, thiết kế với sự hỗ trợ của máy tính CAD (Computer Aided Design).
| THUẬT NGỮ • Mặt phẳng • Điểm thuộc mặt phẳng • Các điểm đồng phẳng • Giao tuyển của hai mặt phẳng • Hình chóp và hình tứ diện | KIẾN THỨC, KĨ NĂNG • Nhận biết các quan hệ liên thuộc cơ bản giữa điểm, đường thẳng, mặt phẳng trong không gian. • Mô tả ba cách xác định mặt phẳng. • Xác định giao tuyến của hai mặt phẳng, giao điểm của đường thẳng và mặt phẳng. • Nhận biết hình chóp và hình tứ diện. • Mô tả một số hình ảnh trong thực tiễn có liên quan đến đường thẳng, mặt phẳng trong không gian. |
Điểm, đường thẳng và mối quan hệ liên thuộc giữa hai đối tượng hình học này đã được giới thiệu trong Hình học phẳng. Bài này tiếp tục trình bày một đối tượng hình học khác là mặt phẳng, đồng thời nghiên cứu mối quan hệ liên thuộc giữa điểm, đường thẳng với mặt phẳng.
Trang 71
1. KHÁI NIỆM MỞ ĐẦU
Mặt bảng, màn hình máy tính hay mặt nước lúc tĩnh lặng là một số hình ảnh về một phần của mặt phẳng. Mặt phẳng không có bề dày và không có giới hạn.

Chú ý
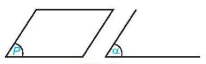
– Để biểu diễn mặt phẳng ta thường dùng một hình binh hành và viết tên của mặt phẳng vào một góc của hình. Ta cũng có thể sử dụng một góc và viết tên của mặt phẳng ở bên trong góc đó.
Hình 4.1
– Để kí hiệu mặt phẳng ta dùng chữ cái in hoa hoặc chữ cái Hy Lạp đặt trong dấu ngoặc ( ). Trong Hình 4.1, ta có mặt phẳng (P) và mặt phẳng (α).
 Hãy tìm một số hình ảnh của mặt phẳng trong thực tế.
Hãy tìm một số hình ảnh của mặt phẳng trong thực tế.
HĐ1. Chấm phạt đền trên sân bóng đá cho ta hình ảnh về một điểm thuộc một mặt phẳng. Hãy tim thêm các ví dụ khác cũng gợi cho ta hình ảnh đó.
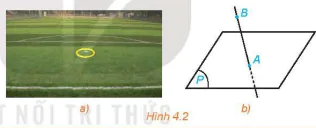
Hình 4.2
| – Điểm A thuộc mặt phẳng (P), kí hiệu A ∈ (P). – Điểm B không thuộc mặt phẳng (P), kí hiệu B ∉ (P). Nếu A ∈ (P) ta còn nói A nằm trên (P), hoặc (P) chứa A, hoặc (P) đi qua A. |
Chú ý. Để nghiên cứu hình học không gian, ta thường về các hình đó lên bảng hoặc lên giẫy. Hình vẽ đó được gọi là hình biểu diễn của một hình không gian. Hình biểu diễn của một hình không gian cần tuân thủ những quy tắc sau:
– Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
– Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.
– Hình biểu diễn giữ nguyên quan hệ liên thuộc giữa điểm và đường thẳng.
– Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn để biểu diễn cho đường bị che khuất.
Các quy tắc khác sẽ được học ở phần sau.
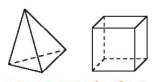
Hình 4.3. Hình biểu diễn của hình chóp tam giác đều và hình lập phương
Trang 72
2. CÁC TÍNH CHẤT THỪA NHẬN
HĐ2. Chiếc xà ngang đặt tựa lên hai điểm A, B của trụ nhảy thể hiện hình ảnh của một đường thẳng đi qua hai điểm đó. Có thể tìm được một đường thằng khác cũng đi qua hai
điểm A, B hay không?

| Có một và chỉ một đường thẳng đi qua hai điểm phân biệt. |
 Có bao nhiêu đường thẳng đi qua hai điểm trong số ba điểm không thẳng hàng?
Có bao nhiêu đường thẳng đi qua hai điểm trong số ba điểm không thẳng hàng?
HĐ3. Trong Hình 4.4 là một khối rubik có bốn đỉnh và bốn mặt, mỗi mặt là một tam giác.

Hình 4.4
a) Đặt khổi rubik sao cho ba đỉnh của mặt màu đỏ đều nằm trên mặt bàn. Khi đó, mặt màu đỏ của khối rubik có nằm trên mặt bàn hay không?
b) Có thể đặt khối rubik sao cho bốn đỉnh của nó đều nằm trên mặt bàn hay không?
| Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng. |
| Tồn tại bốn điểm không cùng thuộc một mặt phẳng. |
Nhận xét. Một mặt phẳng hoàn toàn xác định nếu biết ba điểm không thẳng hàng thuộc mặt phẳng đó. Ta kí hiệu mặt phẳng đi qua ba điểm không thẳng hàng A, B, C là (ABC) cứu định bằng đồng ở cố đô Huế Nếu có nhiều điểm cùng thuộc một mặt phẳng thì ta nói những điểm đó đồng phẳng. Nếu không có mặt phẳng nào chứa các điểm đỗ thì ta nói những điểm đó không đồng phẳng.
 Có bao nhiêu mặt phẳng đi qua ba điểm thẳng hàng?
Có bao nhiêu mặt phẳng đi qua ba điểm thẳng hàng?
Ví dụ 1. Cho bốn điểm A, B, C, D không đồng phẳng (H.4.5). Có bao nhiêu mặt phẳng đi qua ba trong số bốn điểm đã cho?
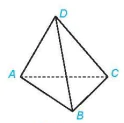
Hình 4.5
Giải
Có 4 mặt phẳng đi qua ba trong số bốn điểm đã cho, đó là các mặt phẳng (DAB), (DAC), (DBC) và (ABC).
Luyện tập 1. Cho tứ giác ABCD. Có bao nhiều mặt phẳng đi qua ba trong số bốn đỉnh của tứ giác đó?
là một di sản văn hoá có giá trị to lớn của Việt Nam.
Vận dụng 1. Hãy giải thích tại sao trong thực tiễn có nhiều đồ vật được thiết kế gồm ba chân như chân đỡ máy ảnh, giá treo tranh, kiềng ba chân treo nổi,...
Trang 73

HĐ4. Căng một sợi dây sao cho hai đầu của sợi dây nằm trên mặt bàn. Khi đó, sợi dây có nằm trên mặt bàn hay không?

| Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó. |
Chú ý. Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói đường thẳng d nằm trong (P) hoặc (P) chứa d. Khi đó ta kí hiệu là d ⊂ (P) hoặc (P) ⊃ d.
Ví dụ 2. Cho tam giác ABC và một điểm M thuộc đường thẳng BC (H.4.6).
a) Điểm M có thuộc mặt phẳng (ABC) hay không?
b) Đường thẳng AM có nằm trong mặt phẳng (ABC) hay không?
Giải
a) Đường thẳng BC có hai điểm phân biệt B, C thuộc mặt phẳng (ABC) nên đường thẳng BC nằm trong mặt phẳng (ABC). Vì M thuộc đường thẳng BC nên M thuộc mặt phẳng (ABC).
b) Đường thẳng AM có hai điểm phân biệt A, M thuộc mặt phẳng (ABC) nên đường thẳng AM nằm trong mặt phẳng (ABC).
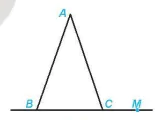
Hình 4.6
Luyện tập 2. Trong Ví dụ 2, lấy điểm N thuộc đường thẳng AB sao cho N khác M. Đường thẳng MN có thuộc mặt phẳng (ABC) hay không?
HĐ5. Trong Hình 4.7, mặt nước và thành bể có giao nhau theo đường thẳng hay không?
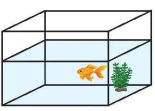
Hình 4.7
Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó.
Chú ý. Đường thẳng chung d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó và kí hiệu là d = (P) ∩ (Q).
Trang 74
Ví dụ 3. Cho tam giác ABC và một điểm S không thuộc mặt phẳng (ABC). Gọi M, N lần lượt là trung điểm của các đoạn thẳng AB, AC (H.4.8).
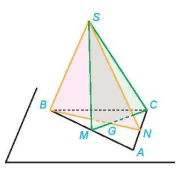
Hình 4.8
a) Chỉ ra một điểm chung của hai mặt phẳng (SBN), (SCM) và khác điểm S.
b) Giao tuyến của hai mặt phẳng (SBN) và (SCM) có đi qua trọng tâm của tam giác ABC hay không?
Giải
a) Trong tam giác ABC, hai đường trung tuyến BN và CM cắt nhau tại trọng tâm G của tam giác. Điểm G thuộc BN nên cũng thuộc mặt phẳng (SBN). Điểm G thuộc CM nên cũng thuộc mặt phẳng (SCM). Vậy G là một điểm chung của hai mặt phẳng (SBN) và (SCM).
b) Vì S, G là hai điểm chung của hai mặt phẳng (SBN) và (SCM) nên giao tuyến của hai mặt phẳng này là đường thằng SG. Đường thẳng này đi qua trọng tâm G của tam giác ABC.
Nhận xét. Hai đường trung tuyến trong một tam giác cắt nhau tại trọng tâm của tam giác là một tính chất đã được học trong hình học phẳng. Trong ví dụ trên, tính chất này đã được áp dụng cho tam giác ABC trong mặt phẳng (ABC). Trong trường hợp tổng quát, ta có tính chất sau:
| Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng. |

Để xác định giao tuyến của hai mặt phẳng, ta tìm hai điểm cùng thuộc cả hai mặt phẳng đó.
Luyện tập 3. Trong Ví dụ 3, hãy xác định giao tuyến của hai mặt phẳng (SBM) và (SCN).
3. CÁCH XÁC ĐỊNH MỘT MẶT PHẲNG SỐNG
Ở mục 2, ta đã thừa nhận kết quả sau:
| - Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng. |
Mục này sẽ tiếp tục giới thiệu thêm hai cách xác định một mặt phẳng.
HĐ6. Cho đường thẳng d và điểm A không thuộc d. Trên đường thẳng d lấy hai điểm phân biệt B, C (H.4.9). Mặt phẳng (ABC) có chứa điểm A và đường thẳng d hay không? Mặt phẳng (ABC) có chứa hai đường thẳng AB và BC hay không?
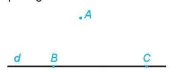
Hình 4.9
| • Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó. • Một mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau. |
Trang 75
Chú ý. Mặt phẳng được xác định bởi điểm A và đường thẳng d không chứa A được kí hiệu là mp(A, d). Mặt phẳng được xác định bởi hai đường thẳng cắt nhau a và b được kí hiệu là mp(a, b).
Ví dụ 4. Cho hai đường thẳng cắt nhau a, b và gọi S là một điểm không thuộc mp(a, b) (H.4.10). Xác định giao tuyến của mp(S, a) và mp(S, b).
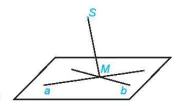
Hình 4.10
Giải
Gọi M là giao điểm của a và b. Vì M thuộc a nên M thuộc mp(S, a). Vì M thuộc b nên M thuộc mp(S, b). Hai điểm S, M cùng thuộc mp(S, a) và mp(S, b) nên giao tuyến của hai mặt phẳng đó là đường thẳng SM.
Luyện tập 4. Trong Ví dụ 4, vẽ một đường thẳng c cắt cả hai đường thẳng a và b. Xác định giao tuyến của hai mặt phẳng: mp(S, a) và mp(S, c); mp(S, b) và mp(S, c).
Vận dụng 2. Để tránh cho cửa ra vào không bị va đập vào các đỗ dùng xung quanh (do mở cửa quả mạnh hoặc do gió to dập cửa), người ta thường sử dụng một phụ kiện là hít của nam châm. Hãy giải thích tại sao khi cửa được hút tới vị trí của nam châm thì cảnh của được giữ cố định.

4. HÌNH CHÓP VÀ HÌNH TỨ DIỆN
HĐ7. Các hình ảnh dưới đây có đặc điểm chung nào với hình chóp tam giác đều mà em đã học ở lớp 8?

• Cho đa giác lồi 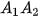 ... ...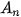 và một điểm S nằm ngoài mặt phẳng chứa đa giác đó. Nối S với các đỉnh và một điểm S nằm ngoài mặt phẳng chứa đa giác đó. Nối S với các đỉnh 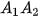 .... .... 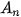 để được n tam giác để được n tam giác 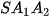 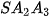 ,...., ,...., 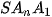 . Hình gồm n tam giác . Hình gồm n tam giác 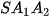 , , 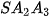 ...., ...., 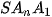 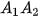 ... ...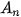 được gọi là hình chóp và kí hiệu là được gọi là hình chóp và kí hiệu là 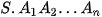 . .• Trong hình chóp 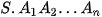 điểm S được gọi là đỉnh và đa giác điểm S được gọi là đỉnh và đa giác 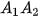 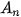 được gọi là mặt đáy, các tam giác được gọi là mặt đáy, các tam giác 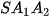 , , 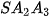 ,..., ,..., 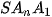 được gọi là các mặt bên; các cạnh được gọi là các mặt bên; các cạnh 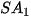 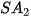 ,..., ,..., 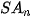 được gọi là các cạnh bên; các cạnh được gọi là các cạnh bên; các cạnh 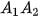 , , 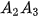 ,..., ,..., 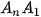 |
Chú ý
Tên của hình chóp được gọi dựa theo tên của đa giác đáy, ví dụ hình chóp có đáy là tứ giác được gọi là hình chóp tứ giác.
Trang 76
Ví dụ 5. Cho hình chóp S.ABCD (H.4.11). Hình chóp đó có bao nhiêu đỉnh, bao nhiêu cạnh?
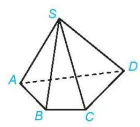
Hình 4.11
Giải
Hình chóp S.ABCD có 5 đỉnh là S, A, B, C, D và có 8 cạnh là SA, SB, SC, SD, AB, BC, CD, DA.
Luyện tập 5. Cho hình chóp S.ABCD. Gọi tên các mặt bên và mặt đáy của hình chóp đó.
HĐ8. Trong các hình chóp ở HĐ7, hình chóp nào có ít đỉnh nhất? Xác định số đỉnh, số cạnh và số mặt của hình chóp đó.
| • Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD được gọi là hình tứ diện và được kí hiệu là ABCD. • Trong hình tứ diện ABCD, các điểm A, B, C, D được gọi là các đỉnh của tứ diện, các đoạn thẳng AB, BC, CD, DA, AC, BD được gọi là các cạnh của tứ diện, các tam giác ABC, ACD, ABD, BCD được gọi là các mặt của tứ diện. • Trong hình tứ diện, hai cạnh không có đỉnh chung được gọi là hai cạnh đối diện, đỉnh không nằm trên một mặt được gọi là đỉnh đối diện với mặt đó. |

Hình tứ diện có bốn mặt là các tam giác đều gọi là hình tứ diện đều.
Nhận xét. Hình tứ diện là một hình chóp tam giác mà mặt nào của hình tứ diện cũng có thể được coi là mặt đáy.
Ví dụ 6. Cho hình tứ diện ABCD và E là một điểm nằm trong tam giác BCD. Gọi F là một điểm nằm giữa A và E (H.4.12). Xác định giao điểm của đường thẳng BF và mặt phẳng là
(ACD).
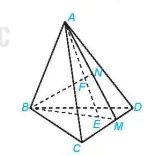
Hình 4.12
Giải
Vì điểm E nằm trong tam giác BCD nên đường thẳng BE cắt cạnh CD tại một điểm M. Các điểm A, E thuộc mặt phẳng (ABM) nên đường thẳng AE thuộc mặt phẳng (ABM), do đó điểm F thuộc mặt phẳng (ABM). Như vậy các điểm A, B, E, F, M cùng thuộc mặt phẳng (ABM).
Trong tam giác ABM, đường thẳng BF cắt AM tại N. Vì N thuộc AM và A, M cùng thuộc mặt phẳng (ACD) nên N thuộc mặt phẳng (ACD). Vậy N là giao điểm của đường thẳng BF và mặt phẳng (ACD).

Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.
Luyện tập 6. Trong Ví dụ 6, xác định giao điểm của đường thẳng DF và mặt phẳng (ABC).
Trang 77
BÀI TẬP
4.1. Trong không gian, cho hai đường thẳng a, b và mặt phẳng (P). Những mệnh đề nào sau đây là đúng?
a) Nếu a chứa một điểm nằm trong (P) thì a nằm trong (P).
b) Nếu a chứa hai điểm phân biệt thuộc (P) thì a nằm trong (P).
c) Nếu a và b cùng nằm trong (P) thì giao điểm (nếu có) của a và b cũng nằm trong (P).
d) Nếu a nằm trong (P) và a cắt b thì b nằm trong (P).
4.2. Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC). Lấy D, E là các điểm lần lượt thuộc các cạnh SA, SB và D, E khác S.
a) Đường thẳng DE có nằm trong mặt phẳng (SAB) không?
b) Giả sử DE cắt AB tại F. Chứng minh rằng F là điểm chung của hai mặt phẳng (SAB) và (CDE).
4.3. Cho mặt phẳng (P) và hai đường thẳng a, b nằm trong (P). Một đường thẳng c cắt hai đường thẳng a và b tại hai điểm phân biệt. Chứng minh rằng đường thẳng c nằm trong mặt phẳng (P).
4.4. Cho hình chóp tứ giác S.ABCD và M là một điểm thuộc cạnh SC (M khác S, C). Giả sử hai đường thẳng AB và CD cắt nhau tại N. Chứng minh rằng đường thẳng MN là giao tuyến của hai mặt phẳng (ABM) và (SCD).
4.5. Cho hình chóp tứ giác S.ABCD và lấy một điểm E thuộc cạnh SA của hình chóp (E khác S, A). Trong mặt phẳng (ABCD) vẽ một đường thẳng d cắt các cạnh CB, CD lần lượt tại M, N và cắt các tia AB, AD lần lượt tại P, Q.
a) Xác định giao điểm của mp(E, d) với các cạnh SB, SD của hình chóp.
b) Xác định giao tuyến mp(E, d) với các mặt của hình chóp.
4.6. Cho hình tứ diện ABCD. Trên các cạnh đường sao cho AM = CM, BN = CN, BP = 2DP.
a) Xác định giao điểm của đường thẳng CD và mặt phẳng (MNP).
b) Xác định giao tuyến của hai mặt phẳng (ACD) và (MNP).
4.7. Tại các nhà hàng, khách sạn, nhân viên phục vụ bản thường xuyên phải bưng bê nhiều khay, đĩa đồ ăn khác nhau. Một trong những nguyên tắc nhân viên cần nhớ là khay phải được bưng bằng ít nhất 3 ngón tay. Hãy giải thích tại sao.

4.8. Bàn cắt giấy là một dụng cụ được sử dụng thường xuyên ở các cửa hàng photo-copy. Bàn cắt giấy gồm hai phần chính: phần bàn hình chữ nhật có chia kích thước giấy và phần dao cắt có một đầu được cố định vào bản. Hãy giải thích tại sao khi sử dụng bàn cắt giấy thì các đường cắt luôn là đường thẳng.











































































Bình Luận
Để Lại Bình Luận Của Bạn