Nội Dung Chính
Trang 88
| THUẬT NGỮ • Đạo hàm của tổng, hiệu • Đạo hàm của tích, thương • Đạo hàm của hàm số hợp • Đạo hàm của các hàm số sơ cấp cơ bản | KIẾN THỨC, KĨ NĂNG • Tính đạo hàm của một số hàm số sơ cấp cơ bản. • Sử dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương các hàm số và đạo hàm của hàm số hợp. • Vận dụng các quy tắc đạo hàm để giải quyết một số bài toán thực tiễn. |
Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu 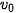
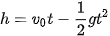
trong đó 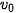 là vận tốc ban đầu của vật, g = 9,8 m/
là vận tốc ban đầu của vật, g = 9,8 m/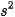 là gia tốc rơi tự do. Hãy tính vận tốc của vật khi nó đạt độ cao cực đại và khi nó chạm đất.
là gia tốc rơi tự do. Hãy tính vận tốc của vật khi nó đạt độ cao cực đại và khi nó chạm đất.
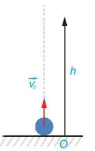
Hình 9.7
1. ĐẠO HÀM CỦA MỘT SỐ HÀM SỐ THƯỜNG GẶP
a) Đạo hàm của hàm số 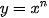 (n ∈ N*}
(n ∈ N*}
HĐ1. Nhận biết đạo hàm của hàm số y = 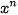
a) Tính đạo hàm của hàm số 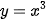 tại điểm x bất kì.
tại điểm x bất kì.
b) Dự đoán công thức đạo hàm của hàm số 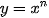 (n ∈ N*).
(n ∈ N*).
Hàm số 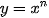 (n ∈ N*) có đạo hàm trên R và (n ∈ N*) có đạo hàm trên R và 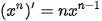 |
b) Đạo hàm của hàm số 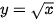
HĐ2. Dùng định nghĩa, tính đạo hàm của hàm số 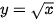 tại điểm x>0.
tại điểm x>0.
Hàm số 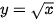 có đạo hàm trên khoảng (0;+∞) và
có đạo hàm trên khoảng (0;+∞) và 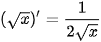 .
.
Ví dụ 1. Tính đạo hàm của hàm số 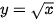
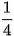 .
. Giải
Với mọi x ∈ (0; +∞), ta có 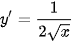 . Do đó
. Do đó 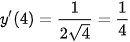 và
và 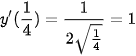 .
.
Trang 89
2. ĐẠO HÀM CỦA TỔNG, HIỆU, TÍCH, THƯƠNG
HĐ3. Nhận biết quy tắc đạo hàm của tổng
a) Dùng định nghĩa, tính đạo hàm của hàm số 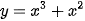
b) So sánh: 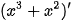 và
và 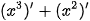
| Giả sử các hàm số u = u (x), v = v (x) có đạo hàm trên khoảng (a; b). Khi đó (u + v)' = u' + v'; (u - v)' = u' - v'; (uv)' = u'v + uv'; 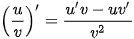 (v = v (x) ≠ 0). (v = v (x) ≠ 0). |
Chú ý
• Quy tắc đạo hàm của tổng, hiệu có thể áp dụng cho tổng, hiệu của hai hay nhiều hàm số.
• Với k là một hằng số, ta có: (ku)' = ku'.
• Đạo hàm của hàm số nghịch đảo 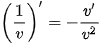 (v = v (x) ≠ 0).
(v = v (x) ≠ 0).
Ví dụ 2. Tính đạo hàm của các hàm số sau:
a) 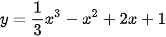
b) 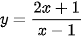 .
.
Giải
a) Ta có: 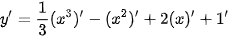
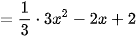
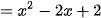 .
.
b) Với mọi x ≠ 1, ta có:
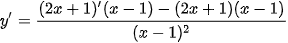
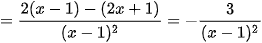 .
.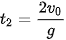
Ví dụ 3. Giải bài toán trong tình huống mở đầu.
Giải
Phương trình chuyển động của vật là 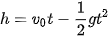 .
.
Vận tốc của vật tại thời điểm t được cho bởi 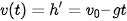 .
.
Vật đạt độ cao cực đại tại thời điểm 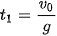
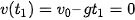 .
. Vật chạm đất tại thời điểm 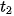 , mà h(
, mà h(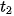 ) = 0 nên ta có:
) = 0 nên ta có:
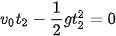 ⇔
⇔ 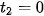
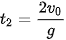 .
. Trang 90
Khi chạm đất, vận tốc của vật là 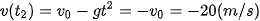 .
.
Dấu âm của 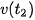 thể hiện độ cao của vật giảm với vận tốc 20 m/s (tức là chiều chuyển động của vật ngược với chiều dương đã chọn).
thể hiện độ cao của vật giảm với vận tốc 20 m/s (tức là chiều chuyển động của vật ngược với chiều dương đã chọn).
Luyện tập 1. Tính đạo hàm của các hàm số sau:
a) 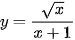 ;
;
b) 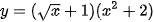
3. ĐẠO HÀM CỦA HÃM SỐ HỢP
a) Khái niệm hàm số hợp
Diện tích của một chiếc đĩa kim loại hình tròn bán kính r được cho bởi S = π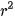 . Bán kính r thay đổi theo nhiệt độ t của chiếc đĩa, tức là r = r (t). Khi đó, diện tích của chiếc đĩa phụ thuộc nhiệt độ S = S (t) = π(r(t))
. Bán kính r thay đổi theo nhiệt độ t của chiếc đĩa, tức là r = r (t). Khi đó, diện tích của chiếc đĩa phụ thuộc nhiệt độ S = S (t) = π(r(t))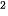 . Ta nói S (t) là hàm số hợp của hàm S = πr
. Ta nói S (t) là hàm số hợp của hàm S = πr với r = r (t).
với r = r (t).
| Giả sử u = g (x) là hàm số xác định trên khoảng (a, b), có tập giá trị chứa trong khoảng (c; d) và y = f (u) là hàm số xác định trên khoảng (c; d). Hàm số y = f (g (x)) được gọi là hàm số hợp của hàm số y = f (u) với u = g (x). |
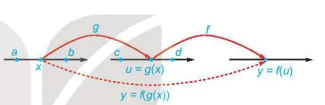
Hình 9.8
Ví dụ 4. Biểu diễn hàm số 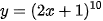
Giải
Hàm số 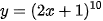 là hàm số hợp của hàm số
là hàm số hợp của hàm số 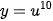 với u = 2x + 1.
với u = 2x + 1.
b) Đạo hàm của hàm số hợp
HĐ4. Nhận biết quy tắc đạo hàm của hàm số hợp
Cho các hàm số 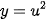 và u = x
và u = x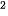 + 1.
+ 1.
a) Viết công thức của hàm số hợp y = (u (x))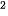
b) Tính và so sánh: y' (x) và y' (u) · u' (x).
Nếu hàm số u = g (x) có đạo hàm 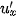 tại x và hàm số y = f (u) có đạo hàm tại tại x và hàm số y = f (u) có đạo hàm tại 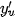 tại u thì hàm số hợp y = f (g (x)) có đạo hàm tại u thì hàm số hợp y = f (g (x)) có đạo hàm 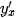 tại x là tại x là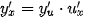 . . |
Ví dụ 5. Tính đạo hàm của hàm số 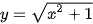
Giải
Đặt u = 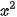 + 1 thì
+ 1 thì 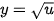 và
và 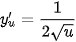 ,
, 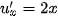 .
.
Trang 91
Theo công thức đạo hàm của hàm số hợp, ta có: 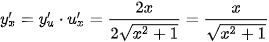
Vậy đạo hàm của hàm số đã cho là 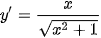 .
.
Trong thực hành, ta thường trình bày ngắn gọn như sau:
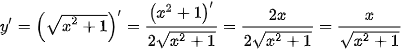 .
.
Luyện tập 2. Tính đạo hàm của các hàm số sau:
a) y = (2x-3)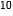 ;
;
b) 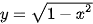
4. ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC
a) Đạo hàm của hàm số y = sin x
HĐ5. Xây dựng công thức tính đạo hàm của hàm số y = sin x
a) Với h ≠ 0, biến đổi hiệu sin(x + h) - sin x thành tích.
b) Sử dụng đẳng thức giới hạn 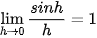
| • Hàm số y = sin x có đạo hàm trên R và (sin x)' = cos x. • Đối với hàm số hợp y = sin u, với u = u (x), ta có: (sin u)' = u' · cos u. |
Ví dụ 6. Tính đạo hàm của hàm số 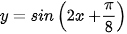 .
.
Giải
Ta có: 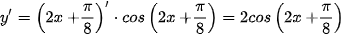 .
.
Luyện tập 3. Tính đạo hàm của hàm số 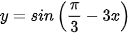 .
.
b) Đạo hàm của hàm số y = cos x
HĐ6. Xây dựng công thức tính đạo hàm của hàm số y = cos x
Bằng cách viết y = cos x = 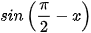 , tính đạo hàm của hàm số y = cos x.
, tính đạo hàm của hàm số y = cos x.
| • Hàm số y = cos x có đạo hàm trên R và (cos x)' = -sin x. • Đối với hàm số hợp y = cos u, với u = u (x), ta có: (cosu)' = –u' · sinu. |
Ví dụ 7. Tính đạo hàm của hàm số 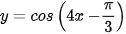
Giải
Ta có: 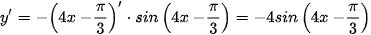 .
.
Trang 92
Luyện tập 4. Tính đạo hàm của hàm số 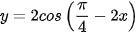 .
.
c) Đạo hàm của các hàm số y = tan x và y = cot x
HĐ7. Xây dựng công thức tính đạo hàm của các hàm số y = tan x và y = cot x
a) Bằng cách viết 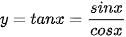 (x ≠
(x ≠ 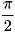 + kπ, k ∈ Z), tính đạo hàm của hàm số y = tan x.
+ kπ, k ∈ Z), tính đạo hàm của hàm số y = tan x.
b) Sử dụng đẳng thức cot x = tan (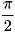
• Hàm số y = tan x có đạo hàm tại mọi x ≠ 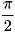 + kπ (k ∈ Z) và + kπ (k ∈ Z) và 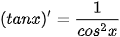 . .• Hàm số y = cot x có đạo hàm tại mọi x ≠ kz (k ∈ Z) và 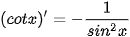 . .• Đối với các hàm số hợp y = tan u và y = cot u, với u = u (x), ta có 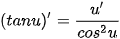 ; ; 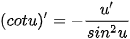 |
Ví dụ 8. Tính đạo hàm của hàm số 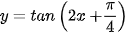 .
.
Giải
Ta có: 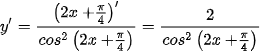 .
.
Luyện tập 5. Tính đạo hàm của hàm số 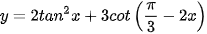
Vận dụng 1. Một vật chuyển độn có phương trình 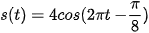 (m), với t là thời gian tính bằng giây. Tính vận tốc của vật khi t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).
(m), với t là thời gian tính bằng giây. Tính vận tốc của vật khi t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).
5. ĐẠO HÀM CỦA HÃM SỐ MŨ VÀ HÀM SỐ LÔGARIT
a) Giới hạn liên quan đến hàm số mũ và hàm số lôgarit
HĐ8. Giới hạn cơ bản của hàm số mũ và hàm số lôgarit
a) Sử dụng phép đổi biến 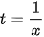
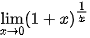 .
. b) Với 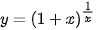 , tính ln y và tìm giới hạn của
, tính ln y và tìm giới hạn của 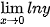 .
.
c) Đặt t = e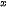 – 1. Tính x theo t và tìm giới hạn
– 1. Tính x theo t và tìm giới hạn 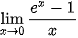
Nhận xét. Ta có các giới hạn sau:
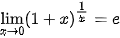 ;
;
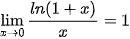 ;
;
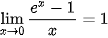 .
.
Trang 93
b) Đạo hàm của hàm số mũ
HD9. Xây dựng công thức tính đạo hàm của hàm số mũ
a) Sử dụng giới hạn 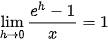 và đẳng thức
và đẳng thức 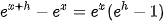
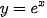 tại x bằng định nghĩa.
tại x bằng định nghĩa. b) Sử dụng đẳng thức 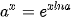 (0 < a ≠ 1), hãy tính đạo hàm của hàm số
(0 < a ≠ 1), hãy tính đạo hàm của hàm số 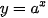 .
.
| • Hàm số 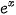 . . Đối với hàm số hợp 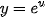 , với u = u (x), ta có: ( , với u = u (x), ta có: (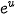 )' = )' = 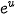 · u'. · u'. • Hàm số 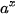 )' = )' = 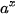 Ina. Ina. Đối với hàm số hợp 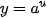 , với u = u (x), ta có: ( , với u = u (x), ta có: (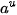 )' = )' = 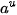 |
Ví dụ 9. Tính đạo hàm của hàm số 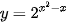 .
.
Giải
Ta có: 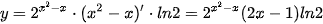 .
.
Luyện tập 6. Tính đạo hàm của các hàm số sau:
a) 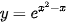 ;
;
b) 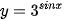
c) Đạo hàm của hàm số lôgarit
HĐ10. Xây dựng công thức tính đạo hàm của hàm số lôgarit
a) Sử dụng giới hạn 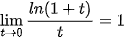
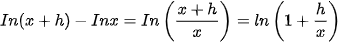 , tính đạo hàm của hàm số y = In x tại điểm x>0 bằng định nghĩa.
, tính đạo hàm của hàm số y = In x tại điểm x>0 bằng định nghĩa. b) Sử dụng đẳng thức 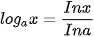 (0 < a ≠ 1), hãy tính đạo hàm của hàm số
(0 < a ≠ 1), hãy tính đạo hàm của hàm số 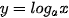 .
.
• Hàm số y = In x có đạo hàm trên khoảng (0; +∞) và 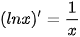 . .Đối với hàm số hợp y = ln u, với u = u (x), ta có: 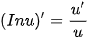 • Hàm số 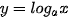 có đạo hàm trên khoảng (0; +∞) và có đạo hàm trên khoảng (0; +∞) và 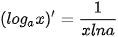 . .Đối với hàm số hợp 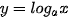 , với u = u (x), ta có: , với u = u (x), ta có: 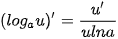 . . |
Chú ý. Với x < 0, ta có: Inlxl = In (-x) và 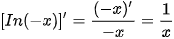
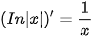 , ∀x ≠ 0).
, ∀x ≠ 0).
Trang 94
Ví dụ 10. Tính đạo hàm của hàm số 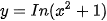 .
.
Giải
=
(x2+1) 2x = x2+1
Vì 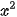 +1 > 0 với mọi x nên hàm số xác định trên R. Ta có:
+1 > 0 với mọi x nên hàm số xác định trên R. Ta có: 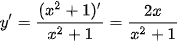 .
.
Luyện tập 7. Tính đạo hàm của hàm số y = log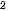
Vận dụng 2. Ta đã biết, độ pH của một dung dịch được xác định bởi pH = -log[H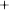 ], ở đó [H
], ở đó [H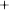 ] là nồng độ (mol) của ion hydrogen. Tính tốc độ thay đổi của pH đối với nồng độ [H
] là nồng độ (mol) của ion hydrogen. Tính tốc độ thay đổi của pH đối với nồng độ [H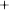
BẢNG ĐẠO HÀM
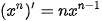 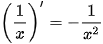 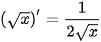 | (sin x)' = cos x (cos x)' = -sin x 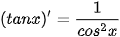 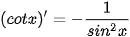 | 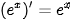 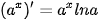 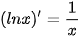 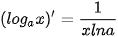 |
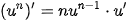 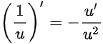 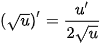 | (sin u)' = u' · cos u (cos u)' = -u' · sin u 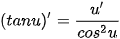 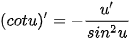 | 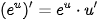 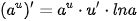 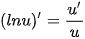 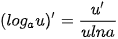 |
BÀI TẬP
9.6. Tính đạo hàm của các hàm số sau:
a) 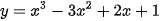 ;
;
b) 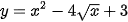 .
.
9.7. Tính đạo hàm của các hàm số sau:
a) 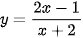 ;
;
b) 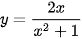
9.8. Tính đạo hàm của các hàm số sau:
a) 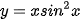 ;
;
b) 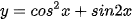 ;
;
c) 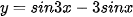 ;
;
d) y = tan x + cot x.
9.9. Tính đạo hàm của các hàm số sau:
a) 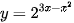 ;
;
b) 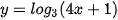
9.10. Cho hàm số 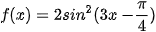 . Chứng minh rằng |f' (x) ≤ 6 với mọi x.
. Chứng minh rằng |f' (x) ≤ 6 với mọi x.
9.11. Một vật chuyển động rơi tự do có phương trình h(t) = 100– 4,9t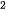 , ở đó độ cao h so với mặt đất tính bằng mét và thời gian t tính bằng giây. Tính vận tốc của vật:
, ở đó độ cao h so với mặt đất tính bằng mét và thời gian t tính bằng giây. Tính vận tốc của vật:
a) Tại thời điểm t = 5 giây.
b) Khi vật chạm đất.
9.12. Chuyển động của một hạt trên một dây rung được cho bởi s(t) = 12 + 0,5 sin (4πt), trong đó s tính bằng centimét và t tính bằng giây. Tính vận tốc của hạt sau t giây. Vận tốc cực đại của hạt là bao nhiêu?










































































Bình Luận
Để Lại Bình Luận Của Bạn