Nội Dung Chính
Trang 61
| THUẬT NGỮ • Thể tích khối hộp • Thể tích khối lăng trụ • Thể tích khối chóp • Thể tích khối chóp cụt | KIẾN THỨC, KĨ NĂNG • Nhận biết công thức tính thể tích của khối chóp, khối lăng trụ, khối hộp, khối chóp cụt đều. • Tính thể tích của khối chóp, khối lăng trụ, khối hộp, khối chóp cụt đều trong một số tình huống đơn giản. • Vận dụng kiến thức, kĩ năng về thể tích vào một số bài toán thực tế. |
Thể tích là một trong những khái niệm toán học xuất hiện thường xuyên trong cuộc sống, đo sự chiếm chỗ của vật thể trong không gian. Bài học này đưa ra công thức thể tích của các hình khối ứng với các hình mà ta đã học.
HĐ1. Khi mua máy điều hoà, bác An được hướng dẫn rằng mỗi mét khối của phòng cần công suất điều hoà khoảng 200 BTU. Căn phòng bác An cần lắp máy có dạng hình hộp chữ nhật, rộng 4 m, dài 5 m và cao 3 m. Hỏi bác An cần mua loại điều hoà có công suất bao nhiêu BTU?

Hình 7.92
| Phần không gian được giới hạn bởi hình chóp, hình chóp cụt đều, hình lăng trụ, hình hộp tương ứng được gọi là khối chóp, khối chóp cụt đều, khối lăng trụ, khối hộp. Đỉnh, mặt, cạnh, đường cao của các khối hình đó lần lượt là đình, mặt, cạnh, đường cao của hình chóp, hình chóp cụt đều, hình lăng trụ, hình hộp tương ứng. • Thể tích của khối chóp có diện tích đáy S và chiều cao h là 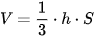 . .• Thể tích của khối chóp cụt đều có diện tích đáy lớn S, diện tích đây bé S' và chiều cao h là 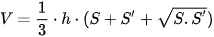 . .• Thể tích của khối lăng trụ có diện tích đáy S và chiều cao h là V = h · S. |
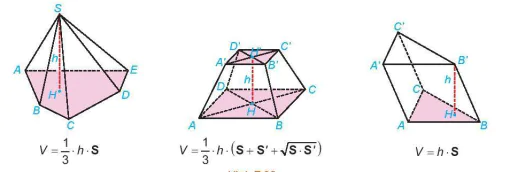
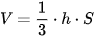
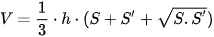
V = h · S
Hình 7.93
Trang 62
Nhận xét
• Thể tích khối tứ diện bằng một phần ba tích của chiều cao từ một đỉnh và diện tích mặt đối diện với đỉnh đó.
• Thể tích của khối hộp bằng tích của diện tích một mặt và chiều cao của khối hộp ứng với mặt đó.
Ví dụ 1. Cho khối tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Tính thể tích của khối tứ diện.
Giải. (H.7.94)
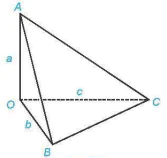
Hình 7.94
Tam giác vuông OBC có diện tích là 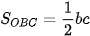 .
.
OA vuông góc với mặt phẳng (OBC) nên tứ diện OABC có chiều cao ứng với đỉnh A bằng OA.
Vậy thể tích của khối tứ diện là 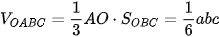 .
.
Luyện tập 1. Cho khối chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích của khối chóp.
Ví dụ 2. Cho khối lăng trụ ABC.A'B'C' có đây là các tam giác đều cạnh a, mặt (ACC'A') vuông góc với hai mặt đáy, tam giác A'AC cân tại A và AA' = b (a < 2b). Tính thể tích của khối lăng trụ.
Giải. (H.7.95)
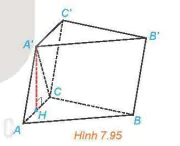
Hình 7.95
Gọi A'H là đường cao của tam giác cân A'AC. Khi đó, H là trung điểm của AC.
Do (ACC'A') ⊥ (ABC) và A'H ⊥ AC nên A'H ⊥ (ABC).
Vậy khối lăng trụ có chiều cao là 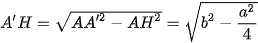
Tam giác đều ABC có diện tích là
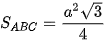 .
. Vậy khối lăng trụ có thể tích là 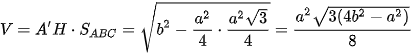 .
.
Luyện tập 2. Cho khối chóp cụt đều ABC.A'B'C' có đường cao HH' = h, hai mặt đáy ABC, A'B'C' có cạnh tương ứng bằng 2a, a.
a) Tính thể tích của khối chóp cụt.
b) Gọi 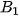 ,
, 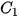 tương ứng là trung điểm của AB, AC. Chứng minh rằng
tương ứng là trung điểm của AB, AC. Chứng minh rằng 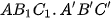
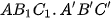 .
. 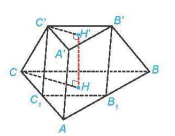
Hình 7.96
Trang 63
Ví dụ 3. Cho khối hộp ABCD.A'B'C'D' có AB = 8 cm, AD = 5 cm, AA' = 6 cm, BAD = 30°, góc giữa AA' và (ABCD) bằng 45°. Tinh thể tích của khối hộp.
Giải. (H.7.97)
Hình binh hành ABCD có diện tích là
2 AB AD sin BAD-20 (cm3).
Gọi H là hình chiếu của A' trên (ABCD). Khi đó, A'AH bằng A góc giữa AA' và (ABCD) nên A'AH = 45°. Trong tam giác
vuông A'AH, ta có A'H = A'A - sin A'AH = 3√2 (cm).
6√2 2
Hình 7.97
Khối hộp ABCD.A'B'C'D' có chiều cao tương ứng với mặt ABCD bằng AH = 32 (cm). Do đó, thể tích của khối hộp là V = A'A - Saeco = 60V2 (cm3).
) Vận dụng. Một sọt đựng đồ có dạng hình chóp cụt đều (H.7.98). Đây và miệng sọt là các hình vuông tương ứng có cạnh bằng 60 cm, 30 cm, cạnh bên của sọt dài 50 cm. Tinh thể tích của sọt.
BÀI TẬP
Hình 7.98
D'
7.28. Cho khối chóp đều S.ABC, đây có cạnh bằng a, cạnh bên bằng b. Tinh thể tích của khối chóp đó. Từ đó suy ra thể tích của khối tử diện đều có cạnh bằng a.
7.29. Cho khối lăng trụ đứng ABC.A'B'C' có AA'= 5 cm, AB = 6 cm, BC = 2 cm, ABC = 150°. Tinh thể tích của khối lăng trụ.
7.30. Cho khối chóp đều S.ABCD, đây có cạnh 6 cm. Tinh thể tích của khối chóp đó trong các trường hợp sau:
a) Cạnh bên tạo với mặt đáy một góc bằng 60%. HỨC
b) Mặt bên tạo với mặt đáy một góc bằng 45.
ING
7.31. Cho khối lăng trụ ABC.A'B'C' có đây là các tam giác đều cạnh a, A'A= AB = A'C = b. Tinh thể tích của khối lăng trụ.
7.32. Từ một tấm tôn hình vuông có cạnh 8 dm, bác Hùng cắt bỏ bốn phần như nhau ở bốn góc, sau đó bác hàn các mép lại để được một chiếc thùng (không có nắp) như Hình 7.99.
a) Giải thích vì sao chiếc thùng có dạng hình chóp cụt.
b) Tinh cạnh bên của thùng.
c) Hỏi thủng có thể chứa được nhiều nhất bao nhiêu lít nước?
1 dm D'
1 dm
3 dm
8 dm
Hình 7.99
B'
C
63









































































Bình Luận
Để Lại Bình Luận Của Bạn