Nội Dung Chính
Trang 54
| THUẬT NGỮ • Khoảng cách • Chiều cao của hình chóp, hình lăng trụ • Đường vuông góc chung | KIẾN THỨC, KĨ NĂNG • Xác định khoảng cách giữa các đối tượng điểm, đường thẳng, mặt phẳng trong không gian. • Xác định đường vuông góc chung của hai đường thẳng chéo nhau trong các trường hợp đơn giản. • Vận dụng kiến thức về khoảng cách vào một số tỉnh huống thực tế. |
Khoảng cách là khái niệm được dùng trong nhiều lĩnh vực của đời sống. Trong bài học này ta tìm hiểu về khoảng cách giữa điểm, đường thẳng, mặt phẳng.

Hình 7.73. Các đầu phun nước chữa cháy Sprinkler cần được lắp đặt theo tiêu chuẩn kĩ thuật, trong đó có tiêu chuẩn về khoảng cách tới từng loại trần, tường, nhà.
1. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG, ĐẾN MỘT MẶT PHẲNG
HĐ1
a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, giải thích vì sao MK ≥ MH (H.7.74).
b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M trên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK ≥ MH (H.7.75).
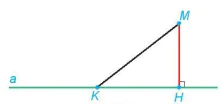
Hình 7.74
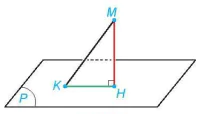
Hình 7.75
| • Khoảng cách từ một điểm M đến một đường thẳng a, kí hiệu d(M, a), là khoảng cách giữa M và hình chiếu H của M trên a. • Khoảng cách từ một điểm M đến một mặt phẳng (P), kí hiệu d(M, (P)), là khoảng cách giữa M và hình chiếu H của M trên (P). |
Chú ý. d(M, a) = 0 khi và chỉ khi M = a, d(M, (P)) = 0 khi và chỉ khi M = (P).
Trang 55
Nhận xét. Khoảng cách từ M đến đường thẳng a (mặt phẳng (P)) là khoảng cách nhỏ nhất giữa M và một điểm thuộc a (thuộc (P)).
Chú ý. Khoảng cách từ đỉnh đến mặt phẳng chứa mặt đáy của một hình chóp được gọi là chiều cao của hình chóp đó.
Ví dụ 1. Cho hình chóp đều S.ABC. Biết độ dài cạnh đáy, cạnh bên tương ứng bằng a, b (a < 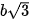 ). Tính chiều cao của hình chóp.
). Tính chiều cao của hình chóp.
Giải. (H.7.76)
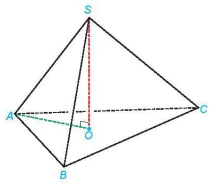
Hình 7.76
Hình chiếu của S trên mặt phẳng (ABC) là tâm O của tam giác đều ABC. Trong tam giác đều ABC, ta có 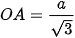
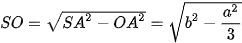 .
. Vậy chiều cao của hình chóp là 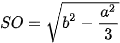 .
.
Luyện tập 1. Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cÂn tại A, AB = a, AA' = h (H.7.77).
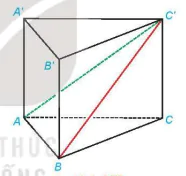
Hình 7.77
a) Tính khoảng cách từ A đến mặt phẳng (BCC'B').
b) Tam giác ABC là tam giác gì? Tính khoảng cách từ A đến BC'.
2. KHOẢNG CÁCH GIỮA CÁC ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG, GIỮA HAI MẶT PHẲNG SONG SONG
HĐ2. Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M, N bắt kì thuộc a và gọi A, B tương ứng là các hình chiếu của chúng
trên (P) (H.7.78).
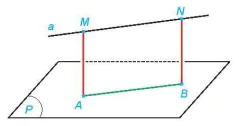
Hình 7.78
Giải thích vì sao ABNM là một hình chữ nhật và M, N có cùng khoảng cách đến (P).
| Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a, kí hiệu d(a, (P), là khoảng cách từ một điểm bất kì trên a đến (P). |
Trang 56
HĐ3. a) Cho hai đường thẳng m và n song song với nhau. Khi một điểm M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n có thay đổi hay không?
b) Cho hai mặt phẳng song song (P) và (Q) và một điểm M thay đổi trên (P) (H.7.79). Hỏi khoảng cách từ M đến (Q) thay đổi thế nào khi M thay đổi.
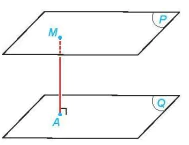
Hình 7.79
| • Khoảng cách giữa hai mặt phẳng song song (P) và (Q), kí hiệu d((P), (Q)), là khoảng cách từ một điểm bắt kĩ thuộc mặt phẳng này đến mặt phẳng kia. • Khoảng cách giữa hai đường thẳng song song m và n, kí hiệu d(m, n), là khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia. |
 Nếu đường thẳng a thuộc mặt phẳng (P) và mặt phẳng (Q) song song với (P) thì giữa d(a, (Q)) và d((P), (Q)) có mối quan hệ gì?
Nếu đường thẳng a thuộc mặt phẳng (P) và mặt phẳng (Q) song song với (P) thì giữa d(a, (Q)) và d((P), (Q)) có mối quan hệ gì?
Chú ý. Khoảng cách giữa hai đáy của một hình lăng trụ được gọi là chiều cao của hình lăng trụ đó.
Ví dụ 2. Cho một hình hộp đứng ABCD.A'B'C'D', đây là các hình thoi có cạnh bằng a, 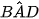 = 120°, AA' = h. Tính các khoảng cách giữa A'C' và (ABCD), AA' và (BDD'B').
= 120°, AA' = h. Tính các khoảng cách giữa A'C' và (ABCD), AA' và (BDD'B').
Giải. (H.7.80)
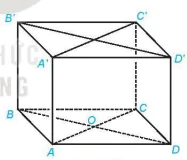
Hình 7.80
Đường thẳng A'C' thuộc mặt phẳng (A'B'C'D') nên nó song song với mặt phẳng (ABCD). Do ABCD.A'B'C'D' là hình hộp đứng nên AA ⊥ (ABCD).
Vậy d(A'C', (ABCD)) = d(A', (ABCD)) = A'A = h.
Do AA' song song với BB nên AA' song song với (BDD'B'). Gọi O là tâm của hình thoi ABCD. Do AO ⊥ BD B và AO ⊥ BB' nên AO ⊥ (BDD'B'). Vậy khoảng cách giữa AA' và (BDD'B') bằng độ dài đoạn thẳng AO. Tam giác BAD cân tại A và có 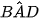 = 120° nên
= 120° nên 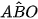
Do đó, trong tam giác vuông AOB, ta có 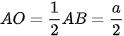 .
.
Vậy khoảng cách giữa AA' và (BDD'B') bằng 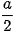 .
.
Luyện tập 2. Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) Tính d((MNP), (ABC)) và d(NP, (ABC)).
b) Giả sử tam giác ABC vuông tại B và AB = a. Tính d(A, (SBC)).
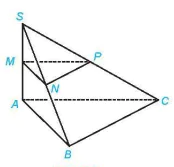
Hình 7.81
Trang 57
Vận dụng. Ở một con dốc lên cầu, người ta đặt một khung khống chế chiều cao, hai cột của khung có phương thẳng đứng và có chiều dài bằng 2,28 m. Đường thẳng nối hai chân cột vuông góc với hai đường mép dốc. Thanh ngang được đặt trên đỉnh hai cột. Biết dốc nghiêng 15° so phương nằm ngang. Tính khoảng cách giữa thanh ngang của khung và mặt đường (theo đơn vị mét và làm tròn kết quả đến chữ số thập phân thứ hai). Hỏi cầu này có
cho phép xe cao 2,21 m đi qua hay không?

Hình 7.82. Tại đầu một số cầu vượt ta có thể bắt gặp khung khống chế chiều cao.
3. KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU
HĐ4. Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).
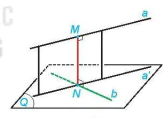
Hình 7.83
a) Mặt phẳng chứa a và a' có vuông góc với (Q) hay không?
b) Đường thẳng MN có vuông góc với cả hai đường thẳng a và b hay không?
c) Nếu mối quan hệ của khoảng cách giữa a, (Q) và độ dài đoạn thẳng MN.
Đường thẳng A cắt hai đường thẳng chéo nhau a, b và vuông góc với cả hai đường thẳng đó được gọi là đường vuông góc chung của a và b.
Nếu đường vuông góc chung A cắt a, b tương ứng tại M, N thì độ dài đoạn thằng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b.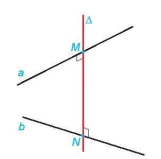
Hình 7.84
Trang 58
Nhận xét
• Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại (H.7.85).
• Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song, tương ứng chứa hai đường thẳng đó (H.7.86).
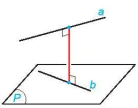
Hình 7.85
Hình 7.86
Ví dụ 3. Cho hình chóp S.ABC có SA ⊥ (ABC), AB = a, 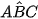 = 60°. Xác định đường vuông góc chung và tính khoảng cách giữa hai đường thẳng SA và BC.
= 60°. Xác định đường vuông góc chung và tính khoảng cách giữa hai đường thẳng SA và BC.
Giải. (H.7.87)
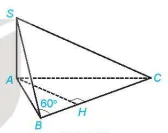
Hình 7.87
Gọi H là hình chiếu của A trên BC. Tam giác ABH vuông tại H và A có AB = a, 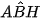 = 60° nên BH =
= 60° nên BH = 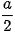 .
.
Do SA vuông góc với mặt phẳng (ABC) nên AH là đường vuông góc chung của SA và BC (H thuộc tia BC và BH = 4). Khoảng cách giữa hai đường thẳng SA và BC là d(SA, BC) = AH = 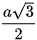 .
.
Khám phá. Cho đường thẳng a vuông góc với mặt phẳng (P) và cắt (P) tại O. Cho đường thẳng b thuộc mặt phẳng (P). Hãy tìm mối quan hệ giữa khoảng cách giữa a, b và khoảng cách từ O đến b (H.7.88).
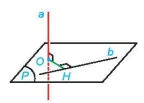
Hình 7.88
Luyện tập 3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD), SA = 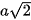
a) Tính khoảng cách từ A đến SC.
b) Chứng minh rằng BD ⊥ (SAC).
c) Xác định đường vuông góc chung và tính khoảng cách giữa BD và SC.
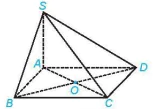
Hình 7.89
Thảo luận. Khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia. Hãy thảo luận để làm rõ nhận xét này.
Trang 59
BÀI TẬP
7.22. Cho hình chóp S.ABCD có đây là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) ⊥ (ABCD).
a) Tính chiều cao của hình chóp.
b) Tính khoảng cách giữa BC và (SAD).
c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.
7.23. Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, BC = c.
a) Tính khoảng cách giữa CC' và (BB'D'D).
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.
7.24. Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) MN là đường vuông góc chung của AB và CD.
b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.
7.25. Cho hình lập phương ABCD.A'B'C'D' có cạnh a.
a) Chứng minh rằng hai mặt phẳng (DAC) và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.
b) Xác định các giao điểm E, F của DB' với (D'AC), (BC'A'). Tính d((D', AC), (BC'A')).
7.26. Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm. Tinh chiều cao của giá đỡ, biết các chân của giá đỡ dài 129 cm.
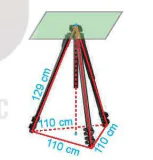
Hình 7.90
7.27. Một bề nước có đáy thuộc mặt phẳng nằm ngang. Trong trường hợp này, độ sâu của bề là khoảng cách giữa mặt nước và đáy bể. Giải thích vì sao để đo độ chiều dài của đoạn dây dọi nằm trong bề nước.
Em có biết?
Vì sao vùng phía bắc chi tuyến Bắc và vùng phía nam chi tuyến Nam tia sáng mặt trời không bao giờ vuông góc với mặt đất (tức là, không xảy ra hiện tượng đứng bóng thực sự tại đó)? (Theo nationalgeographic.com)
Tia sáng mặt trời chỉ vuông góc với mặt đất (tức là có hướng đi qua tâm Trái Đất) tại vị trí 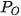 trên mặt đất thuộc đoạn thẳng nối tâm O của Trái Đất và tâm I của Mặt Trời (H.7.91b).
trên mặt đất thuộc đoạn thẳng nối tâm O của Trái Đất và tâm I của Mặt Trời (H.7.91b).
Đường thẳng OI thuộc mặt phẳng chứa quỹ đạo của Trái Đất và trục quay SN (Bắc – Nam) của Trái Đất luôn tạo với mặt phẳng đó một góc khoảng 66,5°. Từ đó ta có thể rút ra 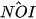 ≥ 66,5°
≥ 66,5°
Mỗi vị trí P thuộc vùng phía bắc chi tuyển Bắc đều có vĩ độ bắc φ > 23,5°, tức là 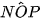
Trang 60
Mặt khác, nếu xảy ra hiện tượng đứng bóng thực sự ở vị trí P thì điểm P thuộc đoạn thẳng OI và do đó 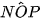 =
= 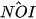 ≥ 66,5°. Điều này dẫn tới mâu thuẫn. Do đó, không thể xảy ra hiện tượng đứng bóng thực sự tại P.
≥ 66,5°. Điều này dẫn tới mâu thuẫn. Do đó, không thể xảy ra hiện tượng đứng bóng thực sự tại P.
Trong mô hình toán học được đề cập ở trên, chúng ta thấy, tại mỗi thời điểm, chỉ có thể xảy ra hiện tượng đứng bóng thực sự tại một vị trí (đó là tại vị trí 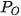 trên mặt đất và thuộc đoạn thẳng OI), do đó, nhìn chung ngay cả ở các vị trí thuộc vùng giữa hai đường chi tuyến Bắc, Nam (có vĩ độ nhỏ hơn 66,5°), trong một năm cũng rất hiếm khi xảy ra hiện tượng đứng bóng thực sự.
trên mặt đất và thuộc đoạn thẳng OI), do đó, nhìn chung ngay cả ở các vị trí thuộc vùng giữa hai đường chi tuyến Bắc, Nam (có vĩ độ nhỏ hơn 66,5°), trong một năm cũng rất hiếm khi xảy ra hiện tượng đứng bóng thực sự.
Tuy vậy, hiện tượng đứng bóng tại một vị trí trên mặt đất được hiểu theo nghĩ rộng hơn; đó là hiện tượng tia sáng mặt trời chiếu trực diện tới Trái Đất tại vị trí đó. Nó xảy ra khi đường kinh tuyến đi qua vị trí đó và tâm I của Mặt Trời cùng thuộc một nửa mặt phẳng bờ NS. Như vậy, tại mỗi vị trí trên mặt đất, mỗi ngày đều xảy ra hiện tượng đứng bóng. Các vị trí thuộc cũng một kinh tuyến thì xảy ra hiện tượng đứng bóng tại cùng một thời điểm, gọi là giữa trưa (trong khoảng 12 giờ trưa cộng, trừ 16 phút).
Góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang tại một vị trí lúc giữa trưa được gọi là góc Mặt Trời (như đã phân tích ở trên, nhìn chung, góc này nhọn). Góc Mặt Trời có ảnh hưởng tới sự hấp thụ nhiệt từ Mặt Trời của Trái Đất, tạo nên các mùa trong năm trên Trái Đất, chẳng hạn vào mùa hè, góc Mặt Trời lớn nên nhiệt độ cao.
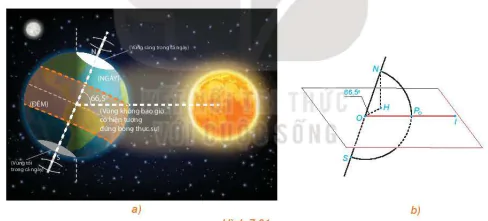
Hình 7.91










































































Bình Luận
Để Lại Bình Luận Của Bạn