Nội Dung Chính
(Trang 12)
| Đèo Hải Vân là một cung đường hiểm trở trên tuyến giao thông xuyên suốt Việt Nam. Để thuận lợi cho việc đi lại, người ta đã xây dựng hầm đường bộ xuyên đèo Hải Vân. Hầm Hải Vân có chiều dài là 6,28 km và bằng (Nguồn: http://www.songda.vn) |
Đèo Hải Vân (Ảnh: kid315) |
 Độ dài của đèo Hải Vân là bao nhiêu ki-lô-mét?
Độ dài của đèo Hải Vân là bao nhiêu ki-lô-mét?
I. CỘNG, TRỪ HAI SỐ HỮU TỈ. QUY TẮC CHUYỂN VỀ
1. Quy tắc cộng, trừ hai số hữu tỉ
1. Thực hiện các phép tính sau:
a) 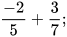 b) 0,123 - 0,234.
b) 0,123 - 0,234.
Nhận xét
Vì mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số. Tuy nhiên, khi hai số hữu tỉ cùng viết ở dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể cộng, trừ hai số đó theo quy tắc cộng, trừ số thập phân.
Ví dụ 1 Tính:
a) 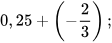 b)
b) 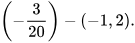
Giải
a) Ta có: 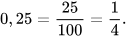
Do đó:
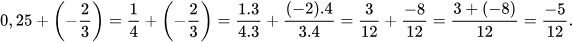
(Trang 13)
Ta có: 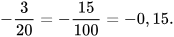
Do đó:
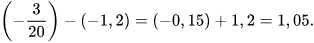
| 1. Tính: a) b) |
2. Tính chất của phép cộng các số hữu tỉ
2 Nêu tính chất của phép cộng các số nguyên.
Nhận xét
• Giống như phép cộng các số nguyên, phép cộng các số hữu tỉ cũng có các tính chất: giao hoán, kết hợp, cộng với số 0, cộng với số đối.
• Ta có thể chuyển phép trừ cho một số hữu tỉ thành phép cộng với số đối của số hữu tỉ đó. Vì thế, trong một biểu thức số chỉ gồm các phép cộng và phép trừ, ta có thể thay đổi tuỳ ý vị trí các số hạng kèm theo dấu của chúng.
Ví dụ 2: Tính một cách hợp lý: 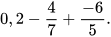
Giải
Ta có: 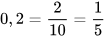 . Do đó:
. Do đó:
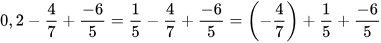
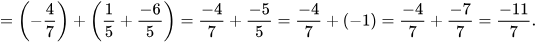
| 2. Tính một cách hợp lý: a) b) |
3. Quy tắc chuyển vế
3
a) Tìm số nguyên x, biết: x + 5 = − 3.
b) Trong tập hợp các số nguyên, nêu quy tắc tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại.
Ta có quy tắc “chuyển vế” đối với số hữu tỉ như sau:
|
x + y = z ⇒ x = z - y; x - y = z ⇒ x = z + y. |
Ví dụ 3: Tìm x, biết:
a) 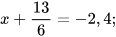 b)
b) 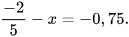
(Trang 14)
Giải
|
Vậy |
Vậy |
| 3. Tìm x, biết: a) b) |
II. NHÂN, CHIA HAI SỐ HỮU TỈ
1. Quy tắc nhân, chia hai số hữu tỉ
4 Thực hiện các phép tính sau:
a) 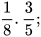
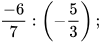 c)
c) 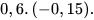
Nhận xét: Vì mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số. Tuy nhiên, khi hai số hữu tỉ cùng viết ở dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể nhân, chia hai số đó theo quy tắc nhân, chia số thập phân.
Ví dụ 4. Tính:
a) 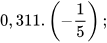 b)
b) 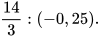
Giải
a) Ta có: 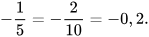
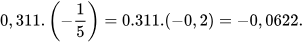
b) Ta có: 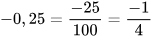 . Do đó:
. Do đó:
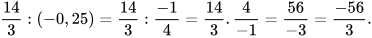
| 4. Giải bài toán trong phần mở đầu. 5. Một ô tô đi từ tỉnh A đến tỉnh B. Trong 1 giờ đầu, ô tô đã đi được |
(Trang 15)
2. Tính chất của phép nhân các số hữu tỉ
5 Nêu tính chất của phép nhân các số nguyên.
Nhận xét: Giống như phép nhân các số nguyên, phép nhân các số hữu tỉ cũng có các tính chất: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân đối với phép cộng và phép trừ.
Ví dụ 5 Tính một cách hợp lí:
a) 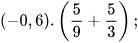
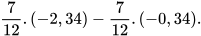
Giải
a) Ta có: 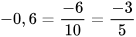 . Do đó:
. Do đó:
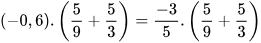
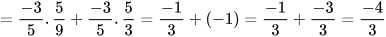 .
.
b) 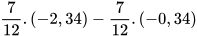
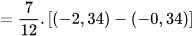
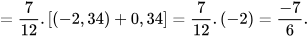
| 6. Tính một cách hợp lí: a) b) |
6 Nêu phân số nghịch đảo của phân số 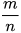
 Mỗi số hữu tỉ a khác 0 đều có số nghịch đảo sao cho tích của số đó với a bằng 1. Mỗi số hữu tỉ a khác 0 đều có số nghịch đảo sao cho tích của số đó với a bằng 1. |
Nhận xét
• Số nghịch đảo của số hữu tỉ a khác 0 kí hiệu là 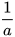 . Ta có:
. Ta có: 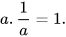
• Số nghịch đảo của số hữu tỉ 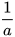 là a.
là a.
• Nếu a, b là hai số hữu tỉ và b ≠ 0 thì 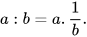
Ví dụ 6 Tìm số nghịch đảo của mỗi số hữu tỉ sau:
a) 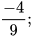 b)
b) 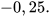
(Trang 16)
Giải
a) Số nghịch đảo của số 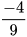 là 1:
là 1: 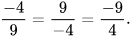
b) Số nghịch đảo của số - 0,25 là 1: (- 0,25) = - 4.
| 7. Tìm số nghịch đảo của mỗi số hữu tỉ sau: a) |
BÀI TẬP
1. Tính:
a) 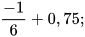 b)
b) 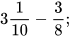 c)
c) 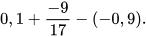
2. Tính:
a) 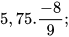 b)
b) 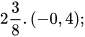
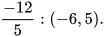
3. Tính một cách hợp lí:
a) 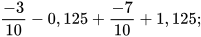 b)
b) 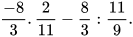
4. Tìm x, biết:
a) 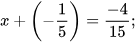 b)
b) 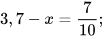
c) 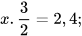 d)
d) 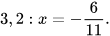
5. Bác Nhi gửi vào ngân hàng 60 triệu đồng với kì hạn 1 năm, lãi suất 6,5%/năm. Hết kì hạn 1 năm, bác rút ra 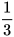 số tiền (kể cả gốc và lãi). Tính số tiền còn lại của bác Nhi trong ngân hàng.
số tiền (kể cả gốc và lãi). Tính số tiền còn lại của bác Nhi trong ngân hàng.
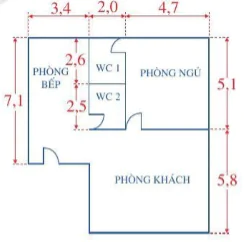
6. Tính diện tích mặt bằng của ngôi nhà trong hình vẽ bên (các số đo trên hình tính theo đơn vị mét).
7. Theo yêu cầu của kiến trúc sư, khoảng cách tối thiểu giữa ổ cắm điện và vòi nước của nhà chú Năm là 60 cm. Trên bản vẽ có tỉ lệ 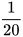
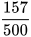

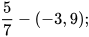
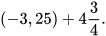
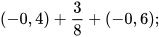
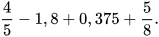
 Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó:
Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: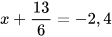
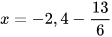
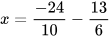
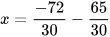
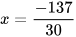
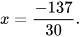
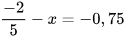
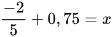
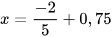
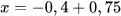
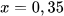
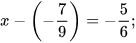
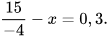
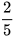 quãng đường. Hỏi với vận tốc đó, ô tô phải mất bao lâu để đi hết quãng đường AB?
quãng đường. Hỏi với vận tốc đó, ô tô phải mất bao lâu để đi hết quãng đường AB?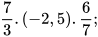
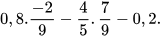
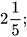



























Bình Luận
Để Lại Bình Luận Của Bạn