Nội Dung Chính
(Trang 44)
Hình 5 mô tả một vật chuyển động từ điểm gốc 0 theo chiều ngược với chiều dương của trục số. Sau 1 giờ, vật đến điểm – 40 trên trục số (đơn vị đo trên trục số là ki-lô-mét).

Hình 5
 | Hỏi vật đã chuyển động được quãng đường là bao nhiêu ki-lô-mét sau 1 giờ. Làm thế nào để biểu diễn được quãng đường đó thông qua số thực – 40? |
I. KHÁI NIỆM
1
a) Hãy biểu diễn hai số – 5 và 5 trên cùng một trục số.
b) Tính khoảng cách từ điểm 5 đến điểm 0.
c) Tính khoảng cách từ điểm – 5 đến điểm 0.
 |
Hình 6 |
 Khoảng cách từ điểm x đến điểm gốc 0 trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu là
Khoảng cách từ điểm x đến điểm gốc 0 trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu là 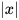
 Giá trị tuyệt đối của một số luôn là một số không âm: |x| ≥ 0 với mọi số thực x. Giá trị tuyệt đối của một số luôn là một số không âm: |x| ≥ 0 với mọi số thực x. |  Hai số thực đối nhau có giá trị tuyệt đối bằng nhau. Hai số thực đối nhau có giá trị tuyệt đối bằng nhau. |
Chẳng hạn, quan sát Hình 6, ta thấy:
– Khoảng cách từ điểm 5 đến điểm gốc 0 là 5 nên giá trị tuyệt đối của số 5 là 5, tức là 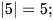
– Khoảng cách từ điểm - 5 đến điểm gốc 0 là 5 nên giá trị tuyệt đối của số - 5 là 5, tức là 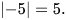
(Trang 45)
Ví dụ 1 Tìm giá trị tuyệt đối của mỗi số thực sau: 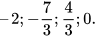
Giải
Ta có biểu diễn trên trục số:

Hình 7
Căn cứ vào khoảng cách từ mỗi điểm 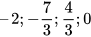 đến điểm gốc 0 trên trục số (Hình 7)
đến điểm gốc 0 trên trục số (Hình 7)
Ta có 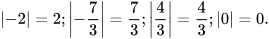
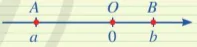
Ví dụ 2 So sánh giá trị tuyệt đối của hai số thực a, b trong mỗi trường hợp sau:
a) 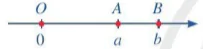
b) 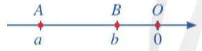
Giải
a) Ta có |a|=OA; |b|=OB.
Do OA < OB nên |a| < |b|.
b) Ta có: |a|=OA; |b|=OB.
Do OA > OB nên |a| > |b|.
| 1 So sánh giá trị tuyệt đối của hai số thực a, b trong mỗi trường hợp sau: a) b) |
II. TÍNH CHẤT
2 Tìm | x | trong mỗi trường hợp sau:
a) x=0,5; b) 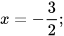 c) x=0; d) x=-4; e) x = 4.
c) x=0; d) x=-4; e) x = 4.
|
• Nếu x là số dương thì giá trị tuyệt đối của x là chính nó: |x| =x(x>0). • Nếu x là số âm thì giá trị tuyệt đối của x là số đối của nó: |x| =−x (x<0). • Giá trị tuyệt đối của 0 là 0: |0| = 0. |
(Trang 46)
Nhận xét: Với mỗi số thực x ta có:
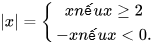
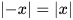 .
.
Ví dụ 3: Tìm:
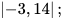
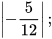
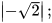
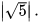
Giải
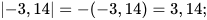
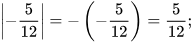
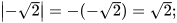
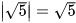 .
.
| 2. Tìm:
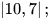
3. Cho x=-12. Tính giá trị của mỗi biểu thức sau: a) 18 + | x |; b) 25 - | x |; c) | 3 + x | - | 7 |. |
Ví dụ 4 Tìm số thực x, biết:
a) | x |= 9; b) | x - 2 | = 0; c) | x+2| =-5.
Giải
a) |x| = 9 nên x=9 hoặc x=−9.
b) |x - 2| = 0 nên x−2=0 hay x=2.
c) Do |x + 2| ≥ 0 với mọi số thực x nên không có số thực x nào thoả mãn |x + 2|=– 5.
Ví dụ 5 Trên trục số, tính độ dài của đoạn thẳng AB trong mỗi trường hợp sau:
a) 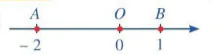 b)
b) 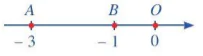
Giải. Ta có:
a) AB = OA + OB = |-2| + |1|=2+1=3;
b) AB = OA-OB=|-3| - |-1| = 3-1=2.
Chú ý: Giả sử hai điểm A, B lần lượt biểu diễn hai số thực a, b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là |a – b|, tức là: AB = |a – b|.
(Trang 47)
1. Tìm 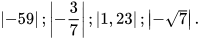
2. Chọn dấu “<”, “>”, “=” thích hợp cho  ?
?
a) | 2,3 | 
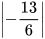 ; b) 9
; b) 9 
 -7,5.
-7,5. 3. Tính giá trị biểu thức:
a) | -137 | + | -363|; b) | -28 | - | 98 |; c) (-200 ) - | -25 | . | 3 |.
4. Tìm x, biết:
a) | x | =4; b) | x | =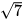 ; c) | x + 5| = 0; d) | x -
; c) | x + 5| = 0; d) | x - 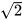 | = 0.
| = 0.
5. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Giá trị tuyệt đối của một số thực là một số dương.
b) Giá trị tuyệt đối của một số thực là một số không âm.
c) Giá trị tuyệt đối của một số thực là số đối của nó.
d) Hai số đối nhau có giá trị tuyệt đối bằng nhau.
6. So sánh hai số a và b trong mỗi trường hợp sau:
a) a, b là hai số dương và |a| < |b|; b) a, b là hai số âm và |a|< |b|.
CÓ THỂ EM CHƯA BIẾT
Khi ta đã biết phép cộng, phép nhân số thực dương thì ta có thể thực hiện phép cộng, phép nhân số thực tuỳ ý. Cụ thể, ta có thể thực hiện phép cộng, phép nhân hai số thực âm hoặc hai số thực khác dấu bằng cách sử dụng giá trị tuyệt đối của số thực.
• Muốn cộng hai số thực âm, ta cộng hai giá trị tuyệt đối của chúng rồi đặt dấu “-” trước kết quả nhận được.
Muốn cộng hai số thực khác dấu không đối nhau, ta tìm hiệu hai giá trị tuyệt đối của chúng (số lớn trừ đi số nhỏ) rồi đặt trước kết quả tìm được dấu của số có giá trị tuyệt đối lớn hơn.
• Muốn nhân hai số thực âm, ta nhân hai giá trị tuyệt đối của chúng.
Muốn nhân hai số thực khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu “-” trước kết quả nhận được.



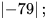
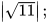
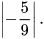




























Bình Luận
Để Lại Bình Luận Của Bạn