Nội Dung Chính
(Trang 17)
|
Hình ảnh Sao Hoả và Trái Đất (Ảnh: BT Image) | Khối lượng Trái Đất khoảng Khối lượng Sao Hoả khoảng (Nguồn: https://www.nasa.gov)
|
I. PHÉP TÍNH LUỸ THỪA VỚI SỐ MŨ TỰ NHIÊN
1 Viết các tích sau dưới dạng luỹ thừa và nêu cơ số, số mũ của chúng:
a) 7.7.7.7.7; b) 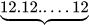 n thừa số 12 (n ∈ N, n> 1).
n thừa số 12 (n ∈ N, n> 1).
Tương tự như đối với số tự nhiên, với số hữu tỉ ta cũng có:
|
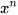 , là tích của n thừa số x: , là tích của n thừa số x:
Số x được gọi là cơ số, n được gọi là số mũ. Quy ước |
Chú ý.
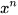 đọc là “x mũ n” hoặc “x luỹ thừa n” hoặc “luỹ thừa bậc n của x”;
đọc là “x mũ n” hoặc “x luỹ thừa n” hoặc “luỹ thừa bậc n của x”;
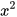
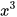 còn được đọc là “x lập phương” hay “lập phương của x”.
còn được đọc là “x lập phương” hay “lập phương của x”.
Ví dụ 1 Viết mỗi tích sau dưới dạng một luỹ thừa:
a) 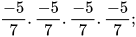
b) 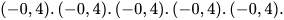
| 1. Tính thể tích một bể nước dạng hình lập phương có độ dài cạnh là 1,8 m. |
(Trang 18)
Giải
Ta có:
a) 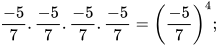
b) 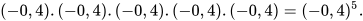
Để viết lũy thừa bậc n của phân số 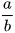 , ta phải viết , ta phải viết 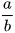 trong dấu ngoặc ( ), tức là trong dấu ngoặc ( ), tức là 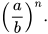 |
| 2. Tính:
|
Ví dụ 2: So sánh:
a) 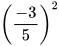
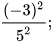
b) 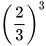 và
và 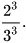
Giải
a) 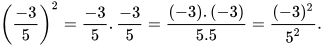
Vậy 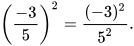
b) 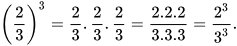
Vậy 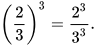
II. TÍCH VÀ THƯƠNG CỦA HAI LUỸ THỪA CÙNG CƠ SỐ
2 Viết kết quả của mỗi phép tính sau dưới dạng một luỹ thừa:
a) 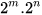 ; b)
; b) 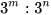 với m ≥n.
với m ≥n.
Cũng như luỹ thừa với cơ số là số tự nhiên, đối với cơ số là số hữu tỉ, ta có các quy tắc sau:
|
• Khi nhân hai luỹ thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:
• Khi chia hai luỹ thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của luỹ thừa bị chia trừ đi số mũ của luỹ thừa chia:
Quy ước: |
(Trang 19)
Ví dụ 3: Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa:
a) 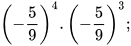 b)
b) 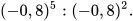
Giải Ta có:
a) 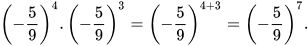
b) 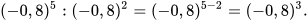
| 3. Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa: a) b) |
III. LŨY THỪA CỦA MỘT LŨY THỪA
3. So sánh: 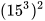
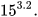
Để so sánh hai số trên, ta làm như sau: 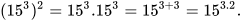
Vậy 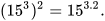
Cũng như vậy, đối với lũy thừa mà cơ số là số hữu tỉ, ta có:
|
|
Ví dụ 4: Viết kết quả mỗi phép tính sau dưới dạng lũy thừa của a:
a) 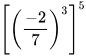 với
với 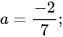 b)
b) 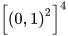 với a = 0,1.
với a = 0,1.
Giải
a) 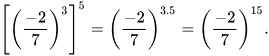
b) 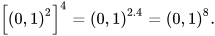
| 4. Viết kết quả mỗi phép tính sau dưới dạng lũy thừa của a: a) b) |
Ví dụ 5: Viết 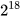 dưới dạng:
dưới dạng:
a) Lũy thừa của 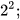
Giải
a) Do 18 = 2 . 9 nên 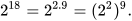
b) Do 18 = 3 . 6 nên 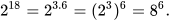
(Trang 20)
BÀI TẬP
1. Tìm số thích hợp cho  trong bảng sau:
trong bảng sau:
| Lũy thừa | 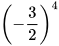 | 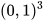 | ? | ? | ? |
| Cơ số | ? | ? | 1,5 | 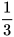 | 2 |
| Số mũ | ? | ? | 2 | 4 | ? |
| Giá trị của lũy thừa | ? | ? | ? | ? | 1 |
2. So sánh:
a) 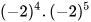 và
và 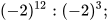 b)
b) 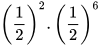 và
và 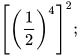
c) 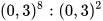 và
và 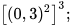 d)
d) 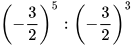 và
và 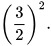
3. Tìm x, biết:
a) 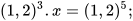
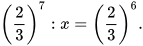
4. Viết kết quả mỗi phép tính sau dưới dạng lũy thừa của a:
a) 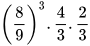 với
với 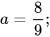 b)
b) 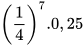 với
với 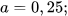
c) 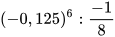 với
với 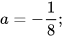 d)
d) 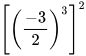 với
với 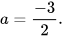
5. Cho x là số hữu tỉ. Viết 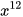
a) Luỹ thừa của 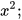 b) Luỹ thừa của
b) Luỹ thừa của 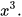
6. Trên bản đồ có tỉ lệ 1 : 100 000, một cánh đồng lúa có dạng hình vuông với độ dài cạnh là 0,7 cm. Tính diện tích thực tế theo đơn vị mét vuông của cánh đồng lúa đó (viết kết quả dưới dạng 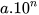 với 1 ≤ a < 10).
với 1 ≤ a < 10).
7. Biết vận tốc ánh sáng xấp xỉ bằng 299 792 458 m/s và ánh sáng Mặt Trời cần khoảng 8 phút 19 giây mới đến được Trái Đất. (Nguồn: https://vi.wikipedia.org)
Khoảng cách giữa Mặt Trời và Trái Đất xấp xỉ bằng bao nhiêu ki-lô-mét?
(Trang 21)
8. Hai mảnh vườn có dạng hình vuông. Mảnh vườn thứ nhất có độ dài cạnh là 19,5 m. Mảnh vườn thứ hai có độ dài cạnh là 6,5 m. Diện tích mảnh vườn thứ nhất gấp bao nhiêu lần diện tích mảnh vườn thứ hai?
9. Chu kì bán rã của nguyên tố phóng xạ Uranium 238 là 4,468 . 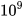 năm (nghĩa là sau 4,468 .
năm (nghĩa là sau 4,468 . 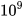
(Nguồn: https://vi.wikipedia.org)
a) Ba chu kì bán rã của nguyên tố phóng xạ đó là bao nhiêu năm?
b) Sau ba chu kì bán rã, khối lượng của nguyên tố phóng xạ đó còn lại bằng bao nhiêu phần khối lượng ban đầu?
10. Người ta thường dùng các luỹ thừa của 10 với số mũ nguyên dương để biểu thị những số rất lớn. Ta gọi một số hữu tỉ dương được viết theo kí hiệu khoa học (hay theo dạng chuẩn) nếu nó có dạng a . 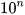 với 1 ≤ a <10 và n là một số nguyên dương. Ví dụ, khối lượng của Trái Đất viết theo kí hiệu khoa học là 5,9724 .
với 1 ≤ a <10 và n là một số nguyên dương. Ví dụ, khối lượng của Trái Đất viết theo kí hiệu khoa học là 5,9724 . 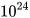 kg.
kg.
Viết các số sau theo kí hiệu khoa học (với đơn vị đã cho):
a) Khoảng cách giữa Mặt Trăng và Trái Đất khoảng 384 400 km;
b) Khối lượng của Mặt Trời khoảng 1 989 . 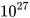 kg;
kg;
c) Khối lượng của Sao Mộc khoảng 1 898 . 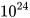 kg.
kg.
(Nguồn: https://www.nasa.gov)
11. Sử dụng máy tính cầm tay
Nút luỹ thừa: 
 )
) Nút phân số: 
Nút chuyển xuống để ghi số hoặc dấu: 
Nút chuyển sang phải để ghi số hoặc dấu: 
| Phép tính | Nút ấn | Kết quả |
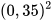 |  | 0,1225 |
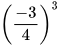 |  | - 0,421875 |
Dùng máy tính cầm tay để tính:
a) 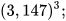 b)
b) 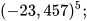
c) 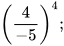 d)
d) 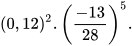
(Trang 22)
Luỹ thừa của một tích, một thương
1. Luỹ thừa của một tích
Với hai số hữu tỉ x và y, ta có:
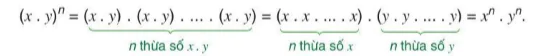
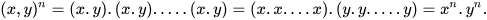
Do đó, ta có công thức:
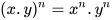
(Lũy thừa của một tích bằng tích các lũy thừa)
2. Luỹ thừa của một thương
Với hai số hữu tỉ x và y (y ≠ 0), ta có:
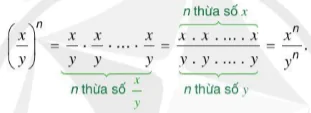
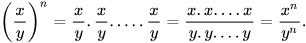
Do đó, ta có công thức:
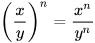 với y ≠ 0, n ∈ N.
với y ≠ 0, n ∈ N.
(Lũy thừa của một thương bằng thương các lũy thừa)
3. Ví dụ
Tính:
a) 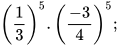 b)
b) 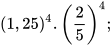
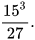
Giải
a) 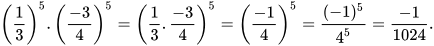
b) 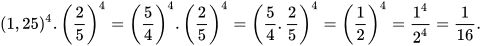
c) 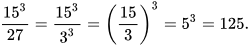

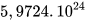 kg.
kg.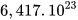 kg.
kg.

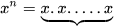 n thừa số x, với n ∈ N*
n thừa số x, với n ∈ N*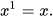
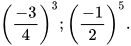

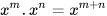 (m, n ∈ N).
(m, n ∈ N).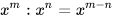 (x ≠ 0; m ≥ n ; m, n ∈ N)
(x ≠ 0; m ≥ n ; m, n ∈ N)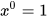 (x ≠ 0).
(x ≠ 0).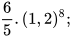
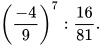
 Khi tích lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ:
Khi tích lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: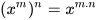
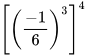 với
với 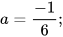
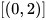 với a = - 0,2
với a = - 0,2


























Bình Luận
Để Lại Bình Luận Của Bạn