Nội Dung Chính
(Trang 90)
Trong chương này, chúng ta sẽ tìm hiểu những nội dung sau: góc ở vị trí đặc biệt; tia phân giác của một góc; hai đường thẳng song song; tiên đề Euclid về đường thẳng song song; định lí, chứng minh định lí.
Trên mặt đồng hồ ở Hình 1, quan sát hai góc: góc tạo bởi kim giờ và kim phút; góc tạo bởi kim phút và kim giây.
Hình 1
 | Hai góc đó có liên hệ gì đặc biệt? |
I. HAI GÓC KỀ NHAU
1 Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy ta vẽ hai tia Oz, Ot như Hình 2.
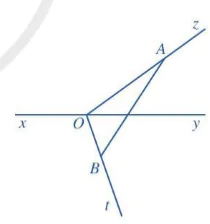
Hình 2
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?
Nhận xét: Hai tia Oz, Ot ở Hình 2 có tính chất sau: Đoạn thẳng AB nối điểm A bất kì trên tia Oz (A khác O) với điểm B bất kì trên tia Ot (B khác O) thì cắt đường thẳng xy. Hai tia Oz và Ot như vậy gọi là nằm về hai phía của đường thẳng xy.
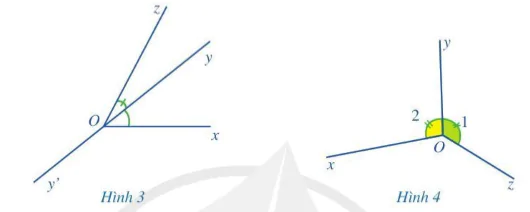
2. Quan sát hai góc xOy và zOy ở Hình 3.
a) Nêu đỉnh chung và cạnh chung của hai góc xOy và zOy.
(Trang 91)
b) Vẽ tia đối Oy' của tia Oy,
c) Hai tia Ox và Oz có nằm về hai phía của đường thẳng yy' hay không?
Nhận xét: Hai góc xOy và zOy ở Hình 3 có tính chất sau: Hai góc đó có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó. Hai góc xOy và zOy như vậy gọi là hai góc kề nhau.
Tương tự, hai góc xOy và zOy ở Hình 4 cũng là hai góc kề nhau.
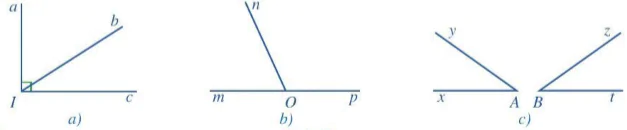
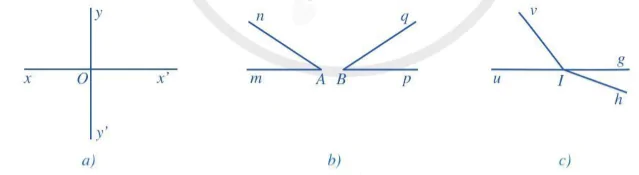
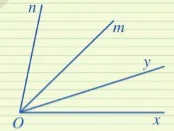
Ví dụ 1 Tìm hai góc kề nhau trong mỗi hình 5a, 5b, 5c, 5d:
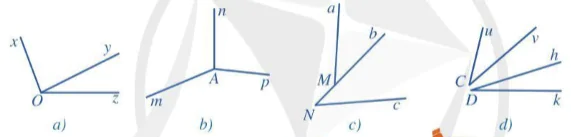
Hình 5
Giải
Ở Hình 5a, hai góc xOy và zOy là hai góc kề nhau.
Ở Hình 5b, các cặp góc kề nhau là mAn và nAp, nAp và pAm, pAm và mAn.
Ở Hình 5c, hai góc aMN và aMb là hai góc kề nhau.
Trong Hình 5, có những cặp góc không phải là hai góc kề nhau, chẳng hạn: cặp góc aMb và bNc, cặp góc aMN và bNc ở Hình 5c; cặp góc uCv và hDk ở Hình 5d, ...
Chú ý: Ta có tính chất sau: Cho góc xOz và tia Oy nằm trong góc đó, tức là mỗi điểm M (M khác O) của tia Oy đều là điểm trong của góc xOz. Khi đó hai góc xOy và yOz là hai góc kề nhau và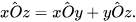 
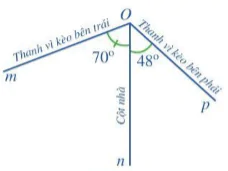
Ví dụ 2 Nhìn bức ảnh ở Hình 7, bạn Quang cho rằng cột nhà tạo với thanh vì kèo bên trái một góc (khoảng) 70° và nó tạo với thanh vì kèo bên phải một góc (khoảng) 48°. Theo dự đoán đó của bạn Quang, hãy tính góc giữa hai thanh vì kèo của mái nhà đó.
| Ở Hình 6, hai góc xOy và mOn có phải là hai góc kề nhau hay không? Vì sao?
Hình 6 |
(Trang 92)
|
Hình 7 |
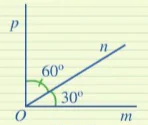
Hình 8 | 2 Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp.
Hình 9 |
Giải
Gọi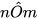 
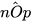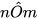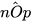là góc tạo bởi cột nhà với thanh vì kèo bên phải (Hình 8). Ta có và là hai góc kề nhau và tổng số đo hai góc đó là: 70° + 48° = 118°. Do đó: 
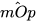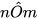
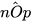= = 118°. Vậy góc giữa hai thanh vì kèo của mái nhà là 118°.
II. HAI GÓC BÙ NHAU. HAI GÓC KỀ BÙ
3 Tìm tổng số đo của góc 110° và góc 70°.
Ta có định nghĩa:
 Hai góc bù nhau là hai góc có tổng số đo bằng 180°. |
4 Quan sát hai góc xOt và yOt ở Hình 10, trong đó Ox và Oy là hai tia đối nhau.
a) Hai góc xOt và yOt có kề nhau hay không?
b) Tính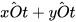 
.
Ta có định nghĩa:
| Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc kề bù. |  |
Chẳng hạn, hai góc xOt và yOt ở Hình 10 là hai góc kề bù.
Ví dụ 3 Tìm hai góc kề bù trong mỗi hình 11a, 11b, 11c:
Hình 11
(Trang 93)
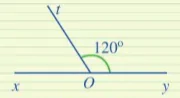
| Giải Ta có: hai góc mOn và nOp ở Hình 116 là hai góc kề bù. Trong Hình 11, có những cặp góc không phải là hai góc kề bù, chẳng hạn: cặp góc aIb và bIc ở Hình 11a; cặp góc xAy và zBt ở Hình 11c; ... | 3 Tính góc xOt trong Hình 12.
Hình 12 |
III. HAI GÓC ĐỐI ĐỈNH
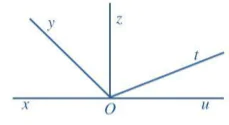
5 Quan sát hai góc xOz và yOt ở Hình 13, trong đó Ox và Oy là hai tia đối nhau, Oz và Ot cũng là hai tia đối nhau và cho biết:
a) Cạnh Ox của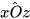 
là tia đối của cạnh nào của 
.
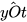b) Cạnh Oz của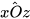 
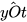. Ta có định nghĩa:
 Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia. |
Chẳng hạn, ở Hình 13, hai góc xOz và yOt là hai góc đối đỉnh, hai góc yOz và xOt cũng là hai góc đối đỉnh.
Ví dụ 4
Tìm hai góc đối đỉnh (khác góc bẹt) trong mỗi hình 14a, 14b, 14c:
Hình 14
Giải
Ở Hình 14a, hai góc xOy và x’O’y’ là hai góc đối đỉnh, hai góc xOy' và x’Oy cũng là hai góc đối đỉnh. Trong Hình 14, có những cặp góc không phải là hai góc đối đỉnh, chẳng hạn: hai góc mAn và pBq ở Hình 14b; hai góc ulv và glh, hai góc vIg và ulh ở Hình 14c; ...
(Trang 94)
6 Quan sát Hình 15 và giải thích vì sao:
Hình 15
a) Hai góc xOy và yOz là hai góc kề bù;
b) Hai góc yOz và zOt là hai góc kề bù;
c)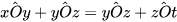 
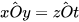.  Hai góc đối đỉnh thì bằng nhau. |
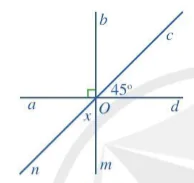
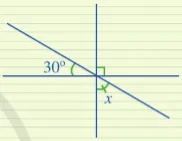
Ví dụ 5 Tìm số đo x trong Hình 16.
|
Hình 16 | 4 Tìm số đo x trong Hình 17
Hình 17 |
Giải
Ta có: Hai góc bOc và cOd là hai góc kề nhau, mà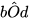 
+ 
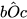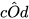=90°. Vì 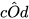= 45° nên 
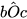= 90° –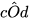 
= 
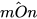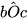. Vậy x = 
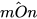= 45°. BÀI TẬP
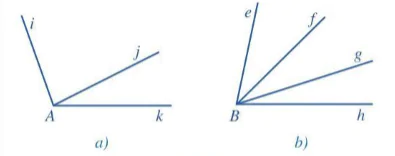
1. a) Tìm các cặp góc kề nhau trong mỗi hình 18a, 18b:
|
Hình 18 |
Hình 19 |
(Trang 95)
c) Tìm hai góc đối đỉnh (khác góc bẹt) trong mỗi hình 20a, 20b, 20c, 20d:
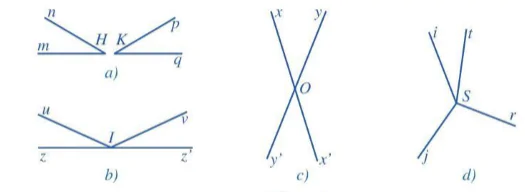
Hình 20
| 2. Quan sát Hình 21 và chỉ ra: a) Hai góc kề nhau; b) Hai góc kề bù; c) Hai góc đối đỉnh. |
Hình 21 |
3. Tìm số đo:
a) Góc mOp trong Hình 22a;
b) Góc qPr trong Hình 22b;
c) x, y trong Hình 22c.
Hình 22
| 4. Hình 23 là một mẫu cửa có vòm tròn của một ngôi nhà. Nếu coi mỗi thanh chắn vòm cửa đó như một cạnh của góc thì các thanh chắn đó tạo ra các góc kề nhau. Theo em, mỗi góc tạo bởi hai thanh chắn vòm cửa đó khoảng bao nhiêu độ? |
Hình 23 |
Bình Luận
Để Lại Bình Luận Của Bạn