(Trang 108)
1. a) Cho một ví dụ về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.
b) Thế nào là tia phân giác của một góc?
c) Cho một ví dụ về hai góc đồng vị, hai góc so le trong.
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có bằng nhau hay không? Hai góc so le trong có bằng nhau hay không?
e) Phát biểu tiên đề Euclid về đường thẳng song song.
2. a) Hai góc có tổng số đo bằng 180° có phải là hai góc kề bù hay không?
b) Hai góc bằng nhau và có chung đỉnh có phải là hai góc đối đỉnh hay không?
3. Tìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d và giải thích vì sao.
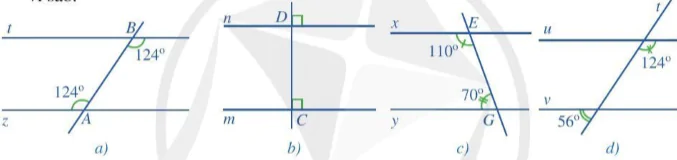
Hình 53
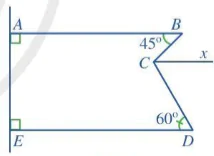
| 4. Quan sát Hình 54, trong đó Cx song song với AB. a) Chứng minh rằng Cx song song với DE. b) Chứng minh rằng c) Tính |
Hình 54 |
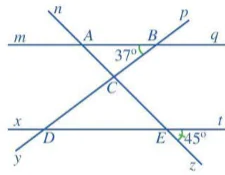
| 5. Quan sát Hình 55, trong đó mq // xt. a) Kể tên các cặp góc đồng vị bằng nhau. b) Tìm số đo các góc BAC, CDE. c) Bạn Nam cho rằng: Qua điểm C kẻ một đường thẳng c song song với hai đường thẳng mq và xt thì sẽ tính được |
Hình 55 |
(Trang 109)
TÌM TÒI – MỞ RỘNG
Nhà toán học Euclid và Hình học mang tên ông
Euclid (còn được biết đến với tên gọi Euclid thành Alexandria) là nhà toán học lỗi lạc thời cổ Hy Lạp. Ông được mệnh danh là “cha đẻ của Hình học". Euclid sinh ở thành Athens (Hy Lạp), sống khoảng 330 – 275 trước Công nguyên. Có rất ít thông tin về cuộc đời ông, chẳng hạn ngày và nơi sinh, cũng như hoàn cảnh cái chết của ông đều không rõ. Bằng cách chọn lọc, phân biệt các kiến thức hình học đã có, bổ sung, khái quát và sắp xếp chúng lại thành một hệ thống chặt chẽ, dùng các tính chất trước để suy ra tính chất sau, bộ sách Cơ sở đồ sộ gồm 13 cuốn của Euclid đã đặt nền móng cho Hình học cũng như toàn bộ Toán học cổ đại. Có thể nói hầu hết kiến thức hình học ở cấp trung học cơ sở hiện nay đều đã được đề cập một cách có hệ thống, chính xác trong bộ sách của ông, và đó cũng là bộ sách có ảnh hưởng nhất trong Lịch sử toán học kể từ khi nó được xuất bản đến đầu thế kỉ XX.
|
Euclid (330 – 275 trước Công nguyên) |
David Hilbert (1862-1943) |
(Nguồn: https://vi.wikipedia.org)
Trong cuốn thứ nhất của bộ sách Cơ sở, Euclid đưa ra năm tiên đề, trong đó một dạng tương đương của Tiên đề 5 chính là tiên đề mà ngày nay chúng ta gọi là Tiên đề Euclid về đường thẳng song song. Với các tiên đề đó, Euclid đã chứng minh được tất cả các tính chất hình học. Tuy nhiên, các tiên đề của Euclid còn quá ít nên trong nhiều chứng minh ông phải dựa vào trực giác hoặc thừa nhận những điều mà ông không nêu thành tiên đề. Năm 1899, nhà toán học vĩ đại người Đức là David Hilbert (1862 – 1943) đã đưa ra hệ tiên đề đầy đủ đầu tiên của Hình học Euclid. Hệ tiên đề đó gồm năm nhóm tiên đề, trong đó đáng lưu ý nhất là nhóm thứ năm chỉ gồm một tiên đề về đường thẳng song song. Ngày nay, ta thường hiểu: Hình học Euclid là hình học thoả mãn tất cả các tiên đề của Euclid, bao gồm cả tiên đề về đường thẳng song song; Hình học phi Euclid không thừa nhận tiên đề về đường thẳng song song đó.
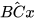 =45° và
=45° và 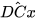 =60°.
=60°.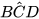 .
.
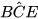





























Bình Luận
Để Lại Bình Luận Của Bạn