Nội Dung Chính
A. Trắc nghiệm
Bài 2.22 trang 56 Toán 11 Tập 1: Khẳng định nào sau đây là sai?
A. Một dãy số tăng thì bị chặn dưới.
B. Một dãy số giảm thì bị chặn trên.
C. Một dãy số bị chặn thì phải tăng hoặc giảm.
D. Một dãy số không đổi thì bị chặn.
Lời giải:
Đáp án đúng là: C
+) Mỗi dãy số tăng đều bị chặn dưới bởi số hạng đầu u1 vì u1 < u2 < u3 < ...., do đó đáp án A đúng.
+) Mỗi dãy số giảm đều bị chặn trên bởi số hạng đầu u1 vì u1 > u2 > u3 > ...., do đó đáp án B đúng.
+) Một dãy số bị chặn không nhất thiết phải là dãy số tăng hoặc giảm. Chẳng hạn ta xét dãy số (un) có số hạng tổng quát ![]()
Ta có nhận xét rằng dãy số này đan dấu nên nó không tăng, không giảm.
Mặt khác ta có: ![]()
Vậy đáp án C sai.
+) Đáp án D đúng do dãy số (un) không đổi thì mọi số hạng luôn bằng nhau và luôn tồn tại m, M để m ≤ un ≤ M với mọi n ∈ ℕ*.
Bài 2.23 trang 56 Toán 11 Tập 1: Cho dãy số ![]() (số hạng sau bằng một nửa số hạng liền trước nó).
(số hạng sau bằng một nửa số hạng liền trước nó).
Công thức tổng quát của dãy số đã cho là
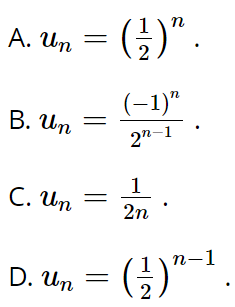
Lời giải:
Đáp án đúng là: D
Xét từng đáp án, ta thấy:
+) Đáp án A, dãy số có số hạng tổng quát là ![]() có số hạng đầu
có số hạng đầu ![]()
+) Đáp án B, dãy số có số hạng tổng quát là ![]() có số hạng đầu
có số hạng đầu ![]() , không thỏa mãn.
, không thỏa mãn.
+) Đáp án C, dãy số có số hạng tổng quát là ![]() có số hạng đầu
có số hạng đầu ![]() , không thỏa mãn.
, không thỏa mãn.
+) Đáp án D, dãy số có số hạng tổng quát là ![]()
Bài 2.24 trang 56 Toán 11 Tập 1: Cho dãy số (un) với un = 3n + 6. Khẳng định nào sau đây là đúng?
A. Dãy số (un) là cấp số cộng với công sai d = 3.
B. Dãy số (un) là cấp số cộng với công sai d = 6.
C. Dãy số (un) là cấp số nhân với công bội q = 3.
D. Dãy số (un) là cấp số nhân với công bội q = 6.
Lời giải:
Đáp án đúng là: A
Ta có: un – un – 1 = (3n + 6) – [3(n – 1) + 6] = 3n + 6 – (3n – 3 + 6) = 3, với mọi n ≥ 2.
Do đó, (un) là cấp số cộng có công sai d = 3.
Bài 2.25 trang 56 Toán 11 Tập 1: Trong các dãy số cho bởi công thức truy hồi sau, dãy số nào là cấp số nhân?
A. u1 = – 1, un+1 = un2
B. u1 = – 1, un + 1 = 2un.
C. u1 = – 1, un + 1 = un + 2.
D. u1 = – 1, un + 1 = un – 2.
Lời giải:
Đáp án đúng là: B
Nhận xét thấy dãy số cho bởi công thức truy hồi u1 = – 1, un + 1 = 2un có ![]() với mọi n ≥ 1. Do đó, dãy số này là một cấp số nhân với số hạng đầu u1 = – 1 và công bội q = 2.
với mọi n ≥ 1. Do đó, dãy số này là một cấp số nhân với số hạng đầu u1 = – 1 và công bội q = 2.
Bài 2.26 trang 56 Toán 11 Tập 1: Tổng 100 số hạng đầu của dãy số (un) với un = 2n – 1 là
A. 199.
B. 2100 – 1.
C. 10 000.
D. 9 999.
Lời giải:
Đáp án đúng là: C
Ta có: un – un – 1 = (2n – 1) – [2(n – 1) – 1] = 2n – 1 – (2n – 2 – 1) = 2, với mọi n ≥ 2.
Do đó, dãy số (un) là một cấp số cộng có u1 = 2 . 1 – 1 = 1 và công sai d = 2.
Tổng 100 số hạng đầu tiên của cấp số cộng này là
![]()
B. Tự luận
Bài 2.27 trang 57 Toán 11 Tập 1: Từ 0 giờ đến 12 giờ trưa, chuông của một chiếc đồng hồ quả lắc sẽ đánh bao nhiêu tiếng, biết rằng nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ?
Lời giải:
Vì đồng hồ đánh chuông báo giờ đúng và số tiếng chuông bằng số giờ nên ta có:
- Lúc 1 giờ đồng hồ đánh 1 tiếng chuông.
- Lúc 2 giờ đồng hồ đánh 2 tiếng chuông.
...
- Lúc 12 giờ trưa đồng hồ đánh 12 tiếng chuông.
Do đó, từ 0 giờ đến 12 giờ trưa, đồng hồ đánh số tiếng chuông là
1 + 2 + 3 + ... + 11 + 12 (tiếng chuông)
Đây là tổng 12 số hạng của cấp số cộng có số hạng đầu u1 = 1, công sai d = 1.
Vậy tổng số tiếng chuông đồng hồ trong khoảng thời gian từ 0 đến 12 giờ trưa là
![]()
Bài 2.28 trang 57 Toán 11 Tập 1: Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Hỏi sau 24 giờ, tế bào ban đầu sẽ phân chia thành bao nhiêu tế bào?
Lời giải:
Vì ban đầu có một tế bào và mỗi lần một tế bào phân chia thành hai tế bào nên ta có cấp số nhân với u1 = 1, q = 2.
Vì cứ 20 phút lại phân đôi một lần nên sau 24 giờ sẽ có 24 . 60 : 20 = 72 lần phân chia tế bào và u73 là số tế bào nhận đươc sau 24 giờ.
Vậy số tế bào nhận được sau 24 giờ phân chia là
u73 = u1 . q72-1 = 1 . 273 – 1 = 272 (tế bào).
Bài 2.29 trang 57 Toán 11 Tập 1: Chứng minh rằng:
a) Trong một cấp số cộng (un), mỗi số hạng (trừ số hạng đầu và số hạng cuối, nếu có) đều là trung bình cộng của hai số hạng đứng kề với nó, nghĩa là
![]()
b) Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và số hạng cuối, nếu có) đều là tích của hai số hạng đứng kề với nó, nghĩa là
uk2 = uk−1 . uk+1 với k ≥ 2.
Lời giải:
a) Giả sử (un) là cấp số cộng với công sai d. Khi đó với k ≥ 2, ta có:
uk – 1 = uk – d và uk + 1 = uk + d.
Suy ra uk – 1 + uk + 1 = (uk – d) + (uk + d) = 2uk hay ![]()
b) Giả sử cấp số nhân có công bội là q. Khi đó với k ≥ 2, ta có:
uk – 1 = u1 . qk – 1 – 1 = u1 . qk – 2;
uk + 1 = u1 . qk + 1 – 1 = u1 . qk.
Suy ra uk – 1 . uk + 1 = (u1 . qk – 2) . (u1 . qk) ![]() (đpcm).
(đpcm).
Bài 2.30 trang 57 Toán 11 Tập 1: Tìm ba số, biết theo thứ tự chúng lập thành cấp số cộng và có tổng bằng 21, và nếu lần lượt cộng thêm các số 2; 3; 9 vào ba số đó thì được ba số lập thành một cấp số nhân.
Lời giải:
Giả sử 3 số cần tìm là x, y, z với x < y < z.
Ta có: x + y + z = 21 ⇒ x + z = 21 – y.
Theo Bài 2.29a, vì x, y, z lập thành một cấp số cộng nên ![]()
Do đó, ![]() Từ đó suy ra y = 7.
Từ đó suy ra y = 7.
Gọi d là công sai của cấp số cộng thì x = y – d = 7 – d và z = y + d = 7 + d.
Sau khi thêm các số 2; 3; 9 vào ba số x, y, z ta được ba số là x + 2, y + 3, z + 9 hay 9 – d, 10, 16 + d và theo đề bài thì 3 số này lập thành một cấp số nhân.
Áp dụng Bài 2.29b, ta có: (9 – d)(16 + d) = 102
⇔ 144 – 7d – d2 = 100
⇔ d2 + 7d – 44 = 0
Giải phương trình bậc hai trên ta được d = – 11 hoặc d = 4.
+) Với d = – 11, ta có cấp số cộng gồm 3 số 18, 7, – 4.
+) Với d = 4, ta có cấp số cộng gồm 3 số 3, 7, 11.
Vậy có hai bộ ba số cần tìm là (18, 7, – 4) và (3, 7, 11).
Bài 2.31 trang 57 Toán 11 Tập 1: Mặt sàn tầng một (tầng trệt) của một ngôi nhà cao hơn mặt sân 0,5 m. Cầu thang đi từ tầng một lên tầng hai gồm 25 bậc, mỗi bậc cao 16 cm.
a) Viết công thức để tìm độ cao của bậc cầu thang thứ n so với mặt sân.
b) Tính độ cao của sàn tầng hai so với mặt sân.
Lời giải:
a) Đổi 16 cm = 0,16 m.
Gọi ui là độ cao từ bậc thang thứ i (của cầu thang) so với mặt sân.
Vì mỗi bậc thang cao 0,16 m, mặt bằng sàn cao hơn mặt sân 0,5 m nên bậc thang đầu tiên sẽ cao hơn so với mặt sân là 0,16 + 0,5 = 0,66 (m) hay u1 = 0,66.
Từ các bậc sau thì: bậc sau cao hơn bậc liền trước nó 0,16 m, nên độ cao so với mặt sân của hai bậc thang liên tiếp cũng hơn kém nhau 0,16 m.
Hay un + 1 = un + 0,16; 1 ≤ n ≤ 25.
Do đó, độ cao từ các bậc thang so với mặt sân, từ bậc 1 đến bậc 25 tạo thành một cấp số cộng với u1 = 0,66 và công sai d = 0,16.
Vậy công thức tính độ cao của bậc cầu thang thứ n so với mặt sân là
un = u1 + (n – 1)d = 0,66 + (n – 1). 0,16 = 0,5 + 0,16n (m).
b) Vì mặt sàn tầng hai có cùng độ cao với bậc thứ 25 (bậc cao nhất) của cầu thang.
Nên độ cao mặt sàn tầng hai so với mặt sân cũng là độ cao từ bậc thứ 25 so với mặt sân.
Vậy độ cao của sàn tầng hai so với mặt sân ứng với n = 25 là
u25 = 0,5 + 0,16 . 25 = 4,5 (m).
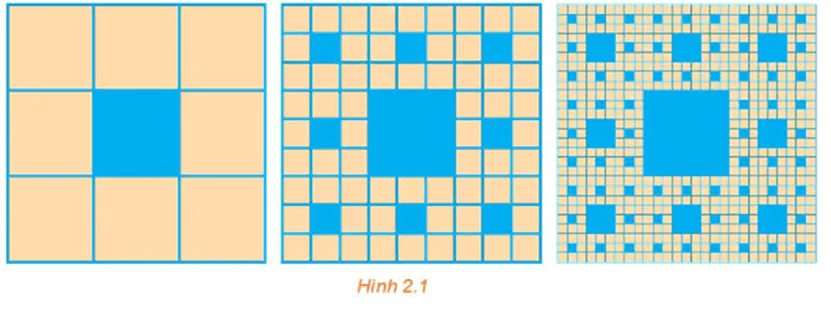
Bài 2.32 trang 57 Toán 11 Tập 1: Một hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1. Mỗi hình vuông màu vàng nhỏ hơn lại được chia thành chín hình vuông con, và mỗi hình vuông con ở chính giữa là được tô màu xanh. Nếu quá trình này được tiếp tục lặp lại năm lần, thì tổng diện tích các hình vuông được tô màu xanh bằng bao nhiêu?
Lời giải:
+ Chia lần 1: Hình vuông màu vàng lớn có cạnh bằng 1 đơn vị thì có diện tích bằng 1 (đvdt). Chia hình vuông này thành 9 hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh, thì hình vuông màu xanh đầu tiên này có diện tích bằng 1/9 (đvdt).
+ Chia lần 2: 8 hình vuông màu vàng còn lại, mỗi hình vuông này lại được chia thành 9 hình vuông con và tiếp tục tô xanh hình vuông chính giữa, khi đó mỗi hình vuông xanh nhỏ hơn có diện tích ![]() , 8 hình vuông xanh nhỏ hơn có diện tích bằng 8S1.
, 8 hình vuông xanh nhỏ hơn có diện tích bằng 8S1.
Cứ tiếp tục như vậy, mỗi lần chia ta sẽ tạo thành 8 hình vuông xanh nhỏ hơn tiếp đối với mỗi ô vuông vàng nhỏ.
Do đó, quá trình này được tiếp tục lặp lại năm lần, thì trừ lần đầu tiên, 4 lần sau, mỗi lần chia diện tích ô vuông xanh tạo thành lập thành một cấp số nhân có ![]() và công bội
và công bội ![]()
Vậy tổng diện tích các hình vuông được tô màu xanh là
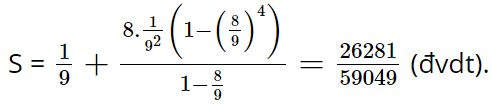










































































Bình Luận
Để Lại Bình Luận Của Bạn