Nội Dung Chính
Mở đầu trang 119 Toán 11 Tập 1: Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km. Chứng tỏ rằng có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.
Lời giải:
Sau bài học này, ta sẽ giải quyết được bài toán trên như sau:
Theo giả thiết, vận tốc trung bình của xe là 
Gọi v(t) là hàm biểu thị vận tốc của xe tại thời điểm t.
Tại thời điểm xuất phát t0, vận tốc của xe v(t0) = 0 nên có một thời điểm t1 xe chạy với vận tốc v(t1) > va.
Xét hàm số f(t) = v(t) – va, rõ ràng f(t) là hàm số liên tục trên đoạn [t0; t1].
Hơn nữa, ta có f(t0) = – va < 0, f(t1) = v(t1) – va > 0 (do v(t1) > va), nên tồn tại thời điểm t* thuộc khoảng (t0; t1) sao cho f(t*) = 0. Khi đó ta có v(t*) – va = 0 hay v(t*) = va = 60.
Vậy có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.
1. Hàm số liên tục tại một điểm
HĐ1 trang 119 Toán 11 Tập 1: Nhận biết tính liên tục của hàm số tại một điểm
Cho hàm số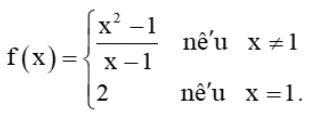 
Tìm giới hạn 
và so sánh giá trị này với f(1).
Lời giải:
Ta có: f(1) = 2.
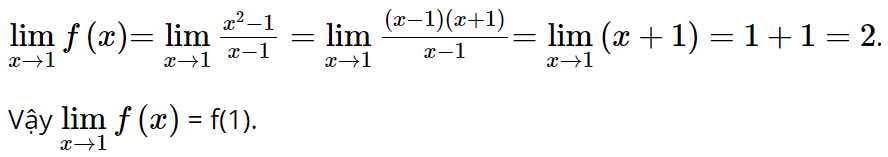
Luyện tập 1 trang 120 Toán 11 Tập 1: Xét tính liên tục của hàm số
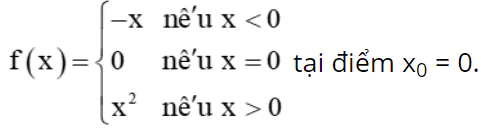
Lời giải:
Hàm số f(x) xác định trên ℝ, do đó x0 = 0 thuộc tập xác định của hàm số.
Ta có: 
Do đó, 
Lại có f(0) = 0 nên 
. Vậy hàm số f(x) liên tục tại x0 = 0.
2. Hàm số liên tục trên một khoảng
HĐ2 trang 120 Toán 11 Tập 1: Cho hai hàm số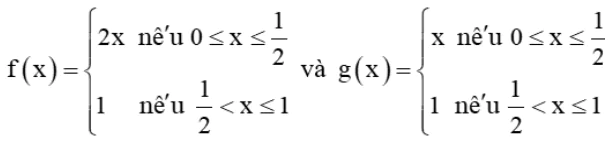 
với đồ thị tương ứng như Hình 5.7.
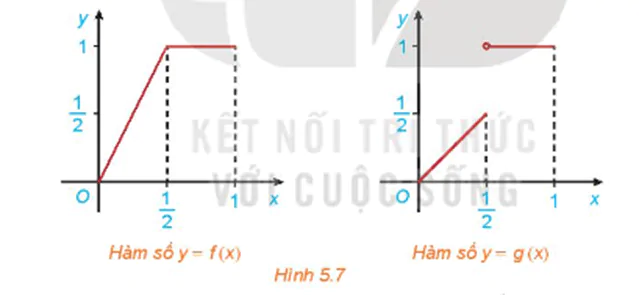
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm 
Lời giải:
+) Hàm số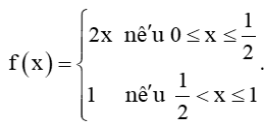 
Hàm số f(x) xác định trên [0; 1], do đó 
thuộc tập xác định của hàm số.
Ta có: 
Suy ra 
Mà 
Vậy hàm số f(x) liên tục tại 
+) Hàm số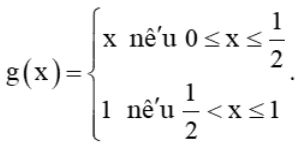 
Hàm số g(x) xác định trên [0; 1], do đó 
thuộc tập xác định của hàm số.
Ta có: 
Suy ra 
Vậy không tồn tại giới hạn của hàm số g(x) tại 
, do đó hàm số g(x) gián đoạn tại 
+) Quan sát Hình 5.7 ta thấy, đồ thị của hàm số y = f(x) là đường liền trên (0; 1), còn đồ thị của hàm số y = g(x) trên (0; 1) là các đoạn rời nhau.
Luyện tập 2 trang 121 Toán 11 Tập 1: Tìm các khoảng trên đó hàm số 
liên tục.
Lời giải:
Biểu thức 
có nghĩa khi x + 2 ≠ 0 hay x ≠ – 2.
Do đó, tập xác định của hàm số f(x) là (–∞; – 2) ∪ (– 2; +∞).
Vậy hàm số f(x) liên tục trên các khoảng (–∞; – 2) và (– 2; +∞).
3. Một số tính chất cơ bản
HĐ3 trang 121 Toán 11 Tập 1: Cho hai hàm số f(x) = x2 và g(x) = – x + 1.
a) Xét tính liên tục của hai hàm số trên tại x = 1.
b) Tính 
Lời giải:
a) Hàm số f(x) = x2 và g(x) = – x + 1 là các hàm đa thức nên nó liên tục trên ℝ.
Do đó, hai hàm số f(x) và g(x) đều liên tục tại x = 1.
b) Ta có: f(x) + g(x) = x2 + (– x + 1) = x2 – x + 1.
Do đó, 
Lại có, f(1) = 12 = 1; g(1) = – 1 + 1 = 0, do đó f(1) + g(1) = 1 + 0 = 1.
Vậy L = f(1) + g(1) = 1.
Vận dụng trang 122 Toán 11 Tập 1: Giải bài toán ở tình huống mở đầu.
Lời giải:
Theo giả thiết, vận tốc trung bình của xe là 
Gọi v(t) là hàm biểu thị vận tốc của xe tại thời điểm t.
Tại thời điểm xuất phát t0, vận tốc của xe v(t0) = 0 nên có một thời điểm t1 xe chạy với vận tốc v(t1) > va.
Xét hàm số f(t) = v(t) – va, rõ ràng f(t) là hàm số liên tục trên đoạn [t0; t1].
Hơn nữa, ta có f(t0) = – va < 0, f(t1) = v(t1) – va > 0 (do v(t1) > va), nên tồn tại thời điểm t* thuộc khoảng (t0; t1) sao cho f(t*) = 0. Khi đó ta có v(t*) – va = 0 hay v(t*) = va = 60.
Vậy có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.
Các Bài Học Khác
Bình Luận
Để Lại Bình Luận Của Bạn