Nội Dung Chính
A. Trắc nghiệm
Bài 5.18 trang 123 Toán 11 Tập 1: Cho dãy số (un) với 
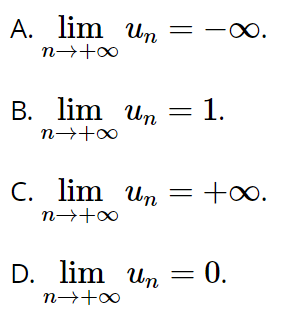
Lời giải:
Đáp án đúng là: C
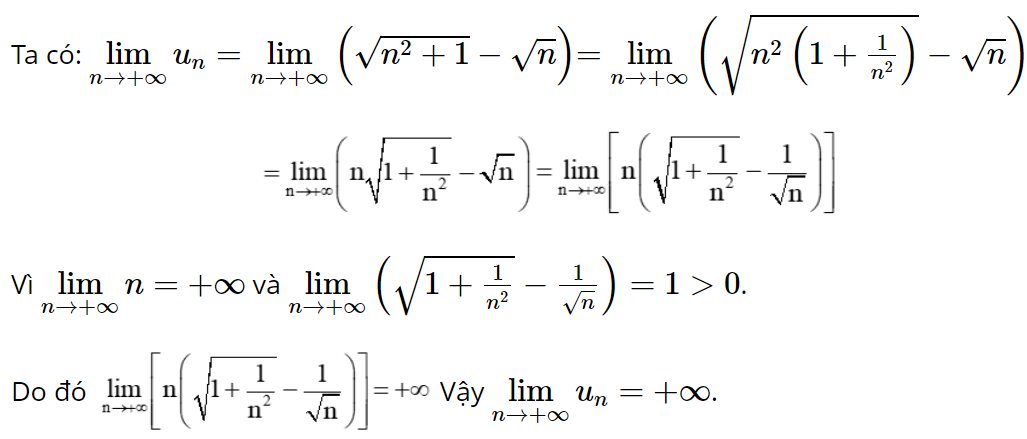
Bài 5.19 trang 123 Toán 11 Tập 1: Cho 
. Giới hạn của dãy số (un) bằng
A. 1.
B. 2.
C. – 1.
D. 0.
Lời giải:
Đáp án đúng là: B
Ta có: 2 + 22 + ... + 2n, đây là tổng của n số hạng đầu của cấp số nhân với số hạng đầu là u1 = 2 và công bội q = 2. Do đó, 2 + 22 + ... + 2n = 
Khi đó, 
Vậy 
Bài 5.20 trang 123 Toán 11 Tập 1: Cho cấp số nhân lùi vô hạn (un) với 
. Tổng của cấp số nhân này bằng
A. 3.
B. 2.
C. 1.
D. 6.
Lời giải:
Đáp án đúng là: C
Ta có: 
, do đó công bội của cấp số nhân là 
Khi đó, tổng của cấp số nhân lùi vô hạn đã cho là 
Bài 5.21 trang 123 Toán 11 Tập 1: Cho hàm số 
. Mệnh đề đúng là
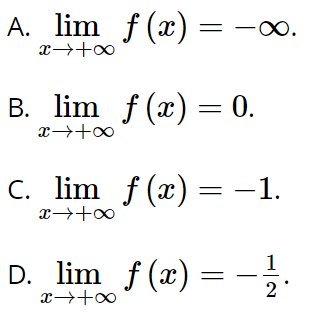
Lời giải:
Đáp án đúng là: B
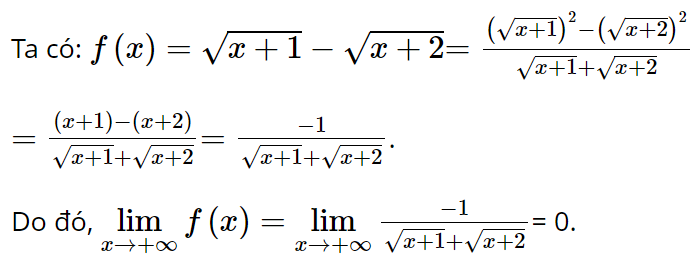
Bài 5.22 trang 123 Toán 11 Tập 1: Cho hàm số 
.
Khi đó 
A. 0.
B. 1.
C. +∞.
D. – 1.
Lời giải:
Đáp án đúng là: B
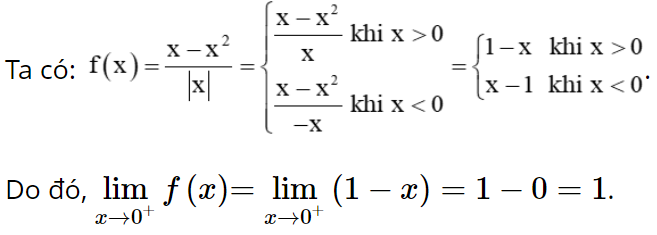
Bài 5.23 trang 123 Toán 11 Tập 1: Cho hàm số 
Hàm số f(x) liên tục trên
A. (–∞; +∞).
B. (–∞; – 1].
C. (–∞; – 1) ∪ (– 1; +∞).
D. [– 1; +∞).
Lời giải:
Đáp án đúng là: C
Ta có: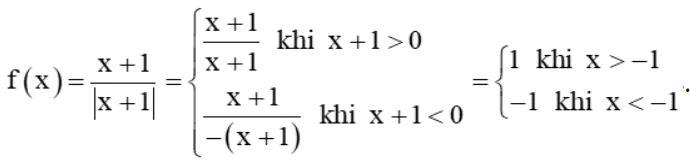 
Tập xác định của hàm số là D = (–∞; – 1) ∪ (– 1; +∞).
Từ đó suy ra hàm số đã cho liên tục trên (–∞; – 1) ∪ (– 1; +∞).
Bài 5.24 trang 123 Toán 11 Tập 1: Cho hàm số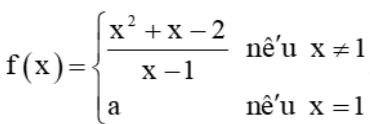 
. Hàm số liên tục tại x = 1 khi
A. a = 0.
B. a = 3.
C. a = – 1.
D. a = 1.
Lời giải:
Đáp án đúng là: B
Ta có: 
f(1) = a.
Để hàm số f(x) liên tục tại x = 1 thì 
B. Tự luận
Bài 5.25 trang 124 Toán 11 Tập 1: Cho dãy số (un) có tính chất 
. Có kết luận gì về giới hạn của dãy số này?
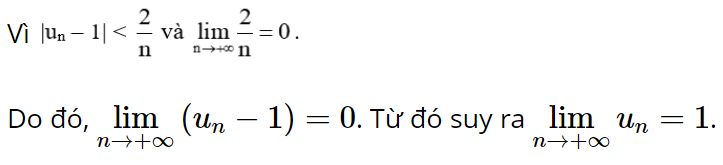
Bài 5.26 trang 124 Toán 11 Tập 1: Tìm giới hạn của các dãy số có số hạng tổng quát cho bởi công thức sau:
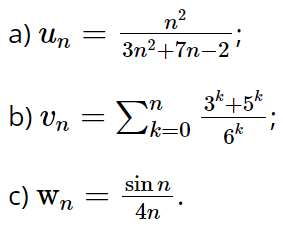
Lời giải:
a) 
Ta có: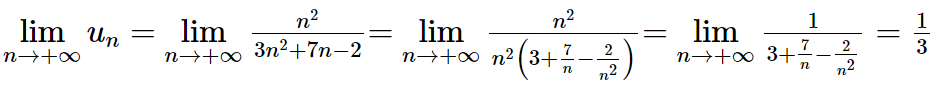 
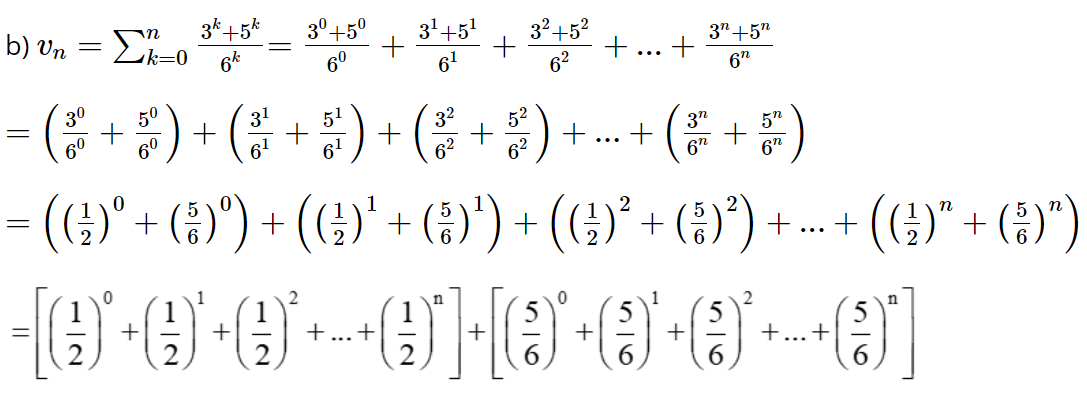
Vì 
là tổng n số hạng đầu của cấp số nhân với số hạng đầu là 
và công bội là 
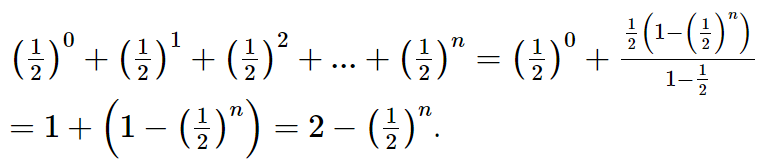
Tương tự, ta tính được:
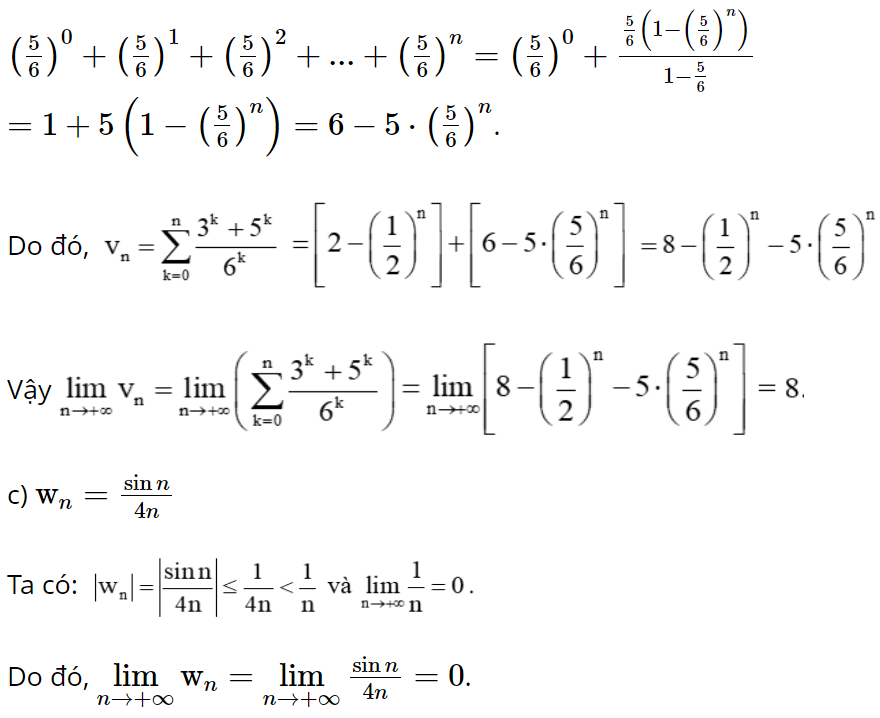
Bài 5.27 trang 124 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số.
a) 1,(01);
b) 5,(132).
Lời giải:
a) Ta có: 1,(01) = 1,010101... = 1 + 0,01 + 0,0001 + 0,000001 + ...
= 100 + 10-2 + 10-4 + 10-6 + ...
Đây là tổng của cấp số nhân lùi vô hạn với u1 = 100 = 1 và q = 10-2 nên
b) Ta có: 5,(132) = 5,132132132... = 5 + 0,132 + 0,000132 + 0,000000132 + ...
= 5 + 0,132 + 0,132 . 10-3 + 0,132 . 10-6 + ...
Vì 0,132 + 0,132 . 10-3 + 0,132 . 10-6 + ... là tổng của cấp số nhân lùi vô hạn với u1 = 0,132 và q = 10-3 nên
0,132 + 0,132 . 10-3 + 0,132 . 10-6 + ... 
Do đó 5,(132) = 5 + 
Bài 5.28 trang 124 Toán 11 Tập 1: Tính các giới hạn sau:
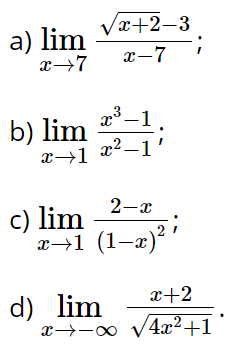
Lời giải:
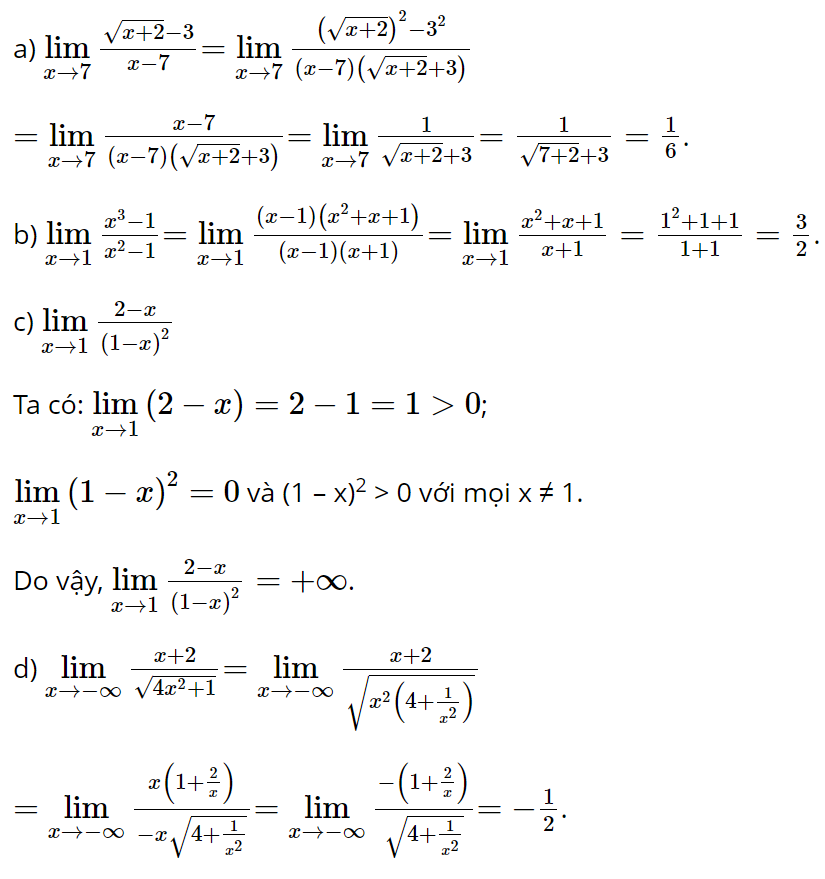
Bài 5.29 trang 124 Toán 11 Tập 1: Tính các giới hạn một bên:
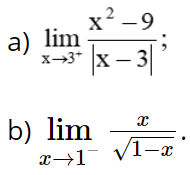
Lời giải:
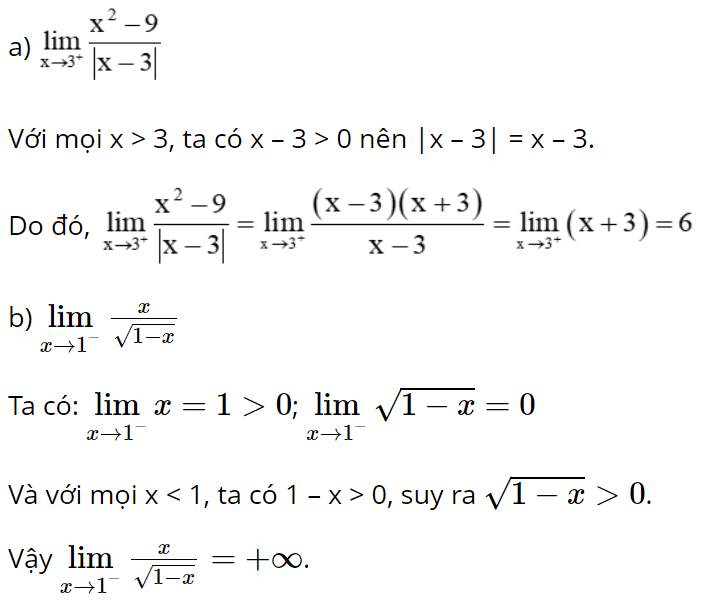
Bài 5.30 trang 124 Toán 11 Tập 1: Chứng minh rằng giới hạn 
Lời giải:
+) Với x > 0, ta có: |x| = x.
Khi đó,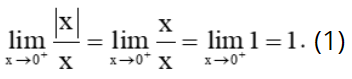 
+) Với x < 0, ta có: |x| = – x.
Khi đó,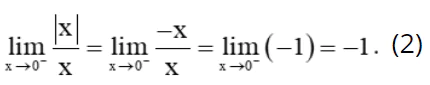 
Từ (1) và (2) suy ra 
nên không tồn tại giới hạn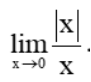 
Bài 5.31 trang 124 Toán 11 Tập 1: Giải thích tại sao các hàm số sau đây gián đoạn tại điểm đã cho.
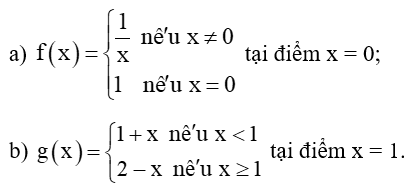
Lời giải:
Bài 5.32 trang 124 Toán 11 Tập 1: Lực hấp dẫn tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm Trái Đất là
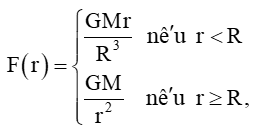
trong đó M và R lần lượt là khối lượng và bán kính của Trái Đất, G là hằng số hấp dẫn. Xét tính liên tục của hàm số F(r).
Lời giải:
Vì M và R lần lượt là khối lượng và bán kính của Trái Đất, G là hằng số hấp dẫn, do đó M, R, G đều khác 0, r là khoảng cách nên r > 0.
Ta có: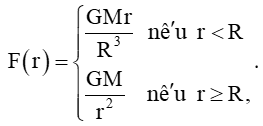 
Tập xác định của hàm số F(r) là (0; +∞).
+) Với r < R thì 
là hàm đa thức nên nó liên tục trên (0; R).
+) Với r > R thì 
+) Tại r = R, ta có 
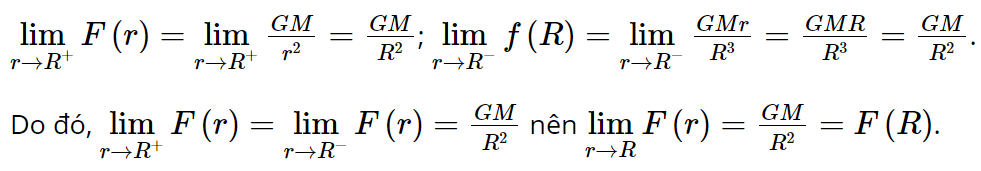
Suy ra hàm số F(r) liên tục tại r = R.
Vậy hàm số F(r) liên tục trên (0; +∞).
Bài 5.33 trang 124 Toán 11 Tập 1: Tìm tập xác định của các hàm số sau và giải thích tại sao các hàm này liên tục trên các khoảng xác định của chúng.
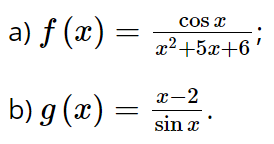
Lời giải:
a) Biểu thức có nghĩa khi x2 + 5x + 6 ≠ 0 ⇔ (x + 2)(x + 3) ≠ 0 
Do đó, tập xác định của hàm số f(x) là ℝ \ {– 3; – 2} = (–∞; – 3) ∪ (– 3; – 2) ∪ (– 2; +∞).
Suy ra hàm số f(x) xác định trên các khoảng (–∞; – 3), (– 3; – 2) và (– 2; +∞). Trên các khoảng này, tử thức (hàm lượng giác) và mẫu thức (hàm đa thức) là các hàm số liên tục. Vậy hàm số 
b) Biểu thức 
có nghĩa khi sin x ≠ 0 ⇔ x ≠ kπ, k ∈ ℤ.
Do đó, tập xác định của hàm số g(x) là ℝ \ {kπ | k ∈ ℤ}. Hay hàm số g(x) xác định trên các khoảng (kπ; (k + 1)π) với k ∈ ℤ.
Trên các khoảng xác định của hàm số g(x), tử thức x – 2 (hàm đa thức) và mẫu thức sin x (hàm lượng giác) là các hàm số liên tục.
Vậy hàm số 
liên tục trên các khoảng xác định của chúng.
Bài 5.34 trang 124 Toán 11 Tập 1: Tìm các giá trị của a để hàm số 
liên tục trên ℝ.
Lời giải:
Ta có: 
Tập xác định của hàm số f(x) là ℝ.
+) Với x < a thì f(x) = x + 1 là hàm đa thức nên nó liên tục trên (–∞; a).
+) Với x > a thì f(x) = x2 là hàm đa thức nên nó liên tục trên (a; +∞).
+) Tại x = a, ta có f(a) = a + 1.
Để hàm số f(x) đã cho liên tục trên ℝ thì f(x) phải liên tục tại x = a, điều này xảy ra khi và chỉ khi 
Suy ra 
Vậy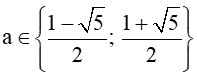 
thì thỏa mãn yêu cầu bài toán.
Các Bài Học Khác
Bình Luận
Để Lại Bình Luận Của Bạn