Nội Dung Chính
A. Trắc nghiệm
Bài 3.8 trang 69 Toán 11 Tập 1:
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Giá trị đại diện của nhóm [20; 40) là
A. 10.
B. 20.
C. 30.
D. 40.
Lời giải:
Đáp án đúng là: C
Giá trị đại diện của nhóm [20; 40) là ![]()
Bài 3.9 trang 69 Toán 11 Tập 1:
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
| Thời gian (phút) | [0; 20) | [20; 40) | [40; 60) | [60; 80) | [80; 100) |
| Số học sinh | 5 | 9 | 12 | 10 | 6 |
Mẫu số liệu ghép nhóm này có số mốt là
A. 0.
B. 1.
C. 2.
D. 3.
Lời giải:
Đáp án đúng là: B
Vì độ dài của các nhóm là bằng nhau và tần số lớn nhất của mẫu số liệu là 12 nên nhóm chứa mốt là nhóm [40; 60). Do đó, mẫu số liệu ghép nhóm này có 1 mốt.
Bài 3.10 trang 69 Toán 11 Tập 1:
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
| Thời gian (phút) | [0; 20) | [20; 40) | [40; 60) | [60; 80) | [80; 100) |
| Số học sinh | 5 | 9 | 12 | 10 | 6 |
Nhóm chứa mốt của mẫu số liệu này là
A. [20; 40).
B. [40; 60).
C. [60; 80).
D. [80; 100).
Lời giải:
Đáp án đúng là: B
Vì độ dài của các nhóm là bằng nhau và tần số lớn nhất của mẫu số liệu là 12 nên nhóm chứa mốt là nhóm [40; 60).
Bài 3.11 trang 69 Toán 11 Tập 1:
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
| Thời gian (phút) | [0; 20) | [20; 40) | [40; 60) | [60; 80) | [80; 100) |
| Số học sinh | 5 | 9 | 12 | 10 | 6 |
Nhóm chứa tứ phân vị thứ nhất là
A. [0; 20).
B. [20; 40).
C. [40; 60).
D. [60; 80).
Lời giải:
Đáp án đúng là: B
Ta có cỡ mẫu là n = 5 + 9 + 12 + 10 + 6 = 42.
Gọi x1, x2, ..., x42 là thời gian tập thể dục trong ngày của 42 học sinh khối 11 và giả sử dãy này đã sắp xếp theo thứ tự tăng dần.
Khi đó tứ phân vị thứ nhất Q1 là trung vị của dãy gồm 21 số liệu đầu nên Q1 = x11. Do x11 thuộc nhóm [20; 40) nên nhóm này chứa Q1.
Bài 3.12 trang 69 Toán 11 Tập 1:
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
| Thời gian (phút) | [0; 20) | [20; 40) | [40; 60) | [60; 80) | [80; 100) |
| Số học sinh | 5 | 9 | 12 | 10 | 6 |
Nhóm chứa trung vị là
A. [0; 20).
B. [20; 40).
C. [40; 60).
D. [60; 80).
Lời giải:
Đáp án đúng là: C
Ta có cỡ mẫu là n = 5 + 9 + 12 + 10 + 6 = 42.
Gọi x1, x2, ..., x42 là thời gian tập thể dục trong ngày của 42 học sinh khối 11 và giả sử dãy này đã sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là ![]() . Do 2 giá trị x21, x22 thuộc nhóm [40; 60) nên nhóm này chứa trung vị Me.
. Do 2 giá trị x21, x22 thuộc nhóm [40; 60) nên nhóm này chứa trung vị Me.
B. Tự luận
Bài 3.13 trang 69 Toán 11 Tập 1: Cơ cấu dân số Việt Nam năm 2020 theo độ tuổi được cho trong bảng sau:
| Độ tuổi | Dưới 5 tuổi | 5 – 14 | 15 – 24 | 25 – 64 | Trên 65 |
| Số người (triệu) | 7,89 | 14,68 | 13,32 | 53,78 | 7,66 |
Chọn 80 là giá trị đại diện cho nhóm trên 65 tuổi. Tính tuổi trung bình của người Việt Nam năm 2020.
Lời giải:
Trong mỗi khoảng độ tuổi, giá trị đại diện là trung bình cộng của giá trị hai đầu mút và đề bài cho 80 là giá trị đại diện cho nhóm trên 65 tuổi nên ta có bảng sau:
| Độ tuổi | 2,5 | 2,5 | 19,5 | 44,5 | 80 |
| Số người (triệu) | 7,89 | 14,68 | 13,32 | 53,78 | 7,66 |
Dân số Việt Nam năm 2020 là 7,89 + 14,68 + 13,32 + 53,78 + 7,66 = 97,33 (triệu người)
Do đó, tuổi trung bình của người Việt Nam năm 2020 là
![]()
Bài 3.14 trang 69 Toán 11 Tập 1: Người ta ghi lại tuổi thọ của một số con ong và cho kết quả như sau:
| Tuổi thọ (ngày) | [0; 20) | [20; 40) | [40; 60) | [60; 80) | [80; 100) |
| Số lượng | 5 | 12 | 23 | 31 | 29 |
Tìm mốt của mẫu số liệu. Giải thích ý nghĩa của giá trị nhận được.
Lời giải:
Tần số lớn nhất là 31 nên nhóm chứa mốt là nhóm [60; 80). Ta có, j = 4, a4 = 60, m4 = 31, m3 = 23, m5 = 29, h = 20. Do đó, mốt của mẫu số liệu ghép nhóm là
![]()
Ý nghĩa: Tuổi thọ của ong khoảng 76 ngày là nhiều nhất hay tuổi thọ chủ yếu của ong là 76 ngày.
Bài 3.15 trang 69 Toán 11 Tập 1: Một bảng xếp hạng đã tính điểm chuẩn hóa cho chỉ số nghiên cứu của một số trường đại học ở Việt Nam và thu được kết quả sau:
| Điểm | Dưới 20 | [20; 30) | [30; 40) | [40; 60) | [60; 80) | [80; 100) |
| Số trường | 4 | 19 | 6 | 2 | 3 | 1 |
Xác định điểm ngưỡng để đưa ra danh sách 25% trường đại học có chỉ số nghiên cứu tốt nhất Việt Nam.
Lời giải:
Cỡ mẫu là n = 4 + 19 + 6 + 2 + 3 + 1 = 35.
Gọi x1, x2, ..., x35 là điểm chuẩn hóa cho chỉ số nghiên cứu của các trường đại học và giả sử dãy này đã sắp xếp theo thứ tự tăng dần. Khi đó, trung vị của mẫu số liệu là Me = x18 và tứ phân vị thứ ba Q3 của mẫu số liệu là trung vị của nửa số liệu bên phải Me, đó là dãy gồm 17 số liệu x19, x20, ..., x35, do đó Q3 = x27. Do x27 thuộc nhóm [30; 40) nên nhóm này chứa Q3. Do đó, p = 3; a3 = 30; m3 = 6; m1 + m2 = 4 + 19 = 23; a4 – a3 = 40 – 30 = 10 và ta có
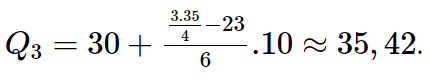
25% trường đại học có chỉ số nghiên cứu tốt nhất là 25% giá trị nằm bên phải Q3.
Vậy điểm ngưỡng để đưa ra danh sách 25% trường đại học có chỉ số nghiên cứu tốt nhất Việt Nam là những trường có điểm chuẩn hóa lớn hơn hoặc bằng 35,42.











































































Bình Luận
Để Lại Bình Luận Của Bạn